Бармалей. 1 категория

• Название: 1 категория
• Анкор: Бармалей
• Дата: 09.02.2023
• Размер: 0.59 Mb.
• Имя файла: 1_Lineynaya_algebra_baza_spets.doc
• Тип: Документы; #927960
• страница: 3 из 6

Какое преобразование не может изменить ранг матрицы?

1. Удаление из матрицы какого-либо её столбца

2. Замена всех её строк строками, состоящими полностью из нулей

3. Перемена местами двух элементов матрицы

4. Транспонирование матрицы

45. 
    
    

Укажите неверное в общем случае соотношение для квадратной матрицы A ( Е – единичная матрица, 0 – нулевая матрица)

1. 
   2. 3.
   

4.

46. 
    
    

Даны матрицы и и вещественное число .

Тогда , если …

1. 2.

3. 4.

( - элементы матриц A и C)

47. 
    
    

Указать невырожденную

матрицу А

1. 2.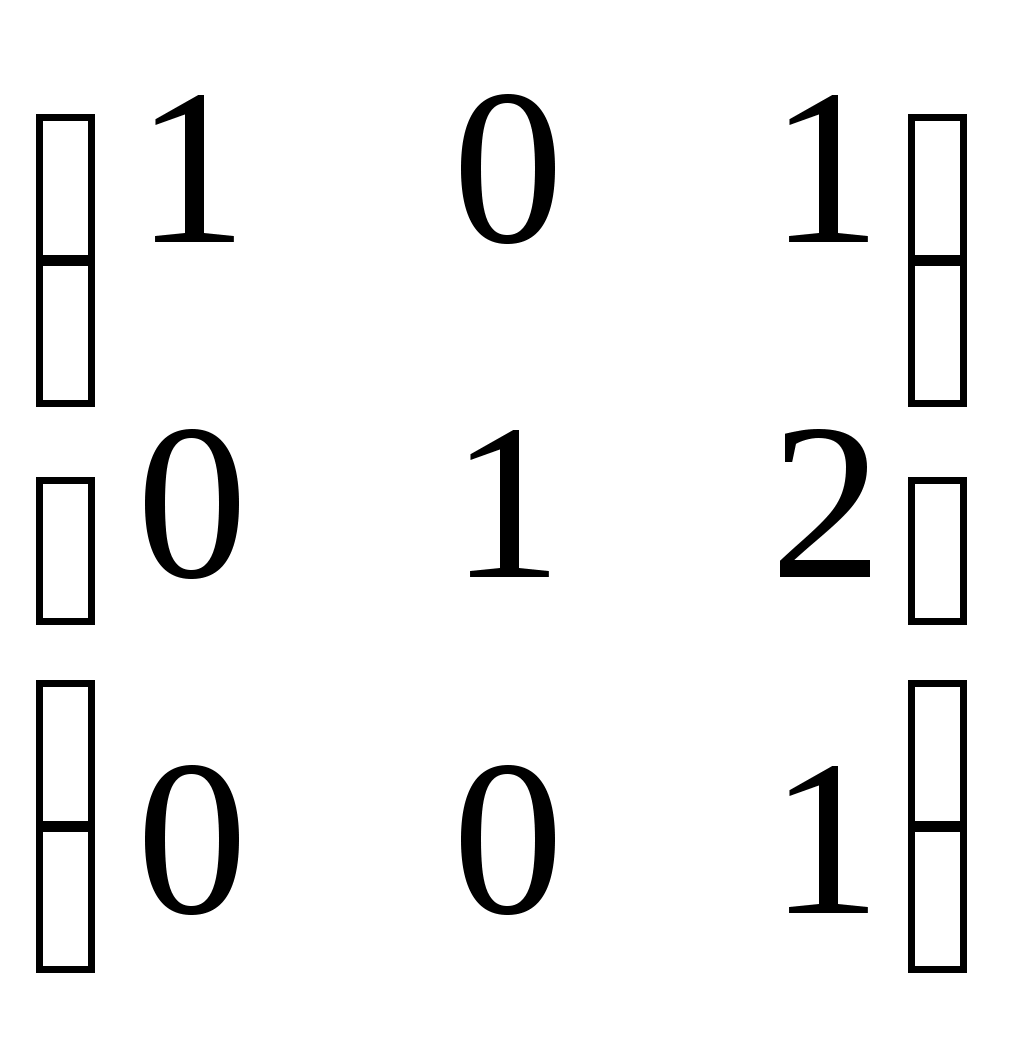

3. 4.

48. 
    
    

Ранг матрицы 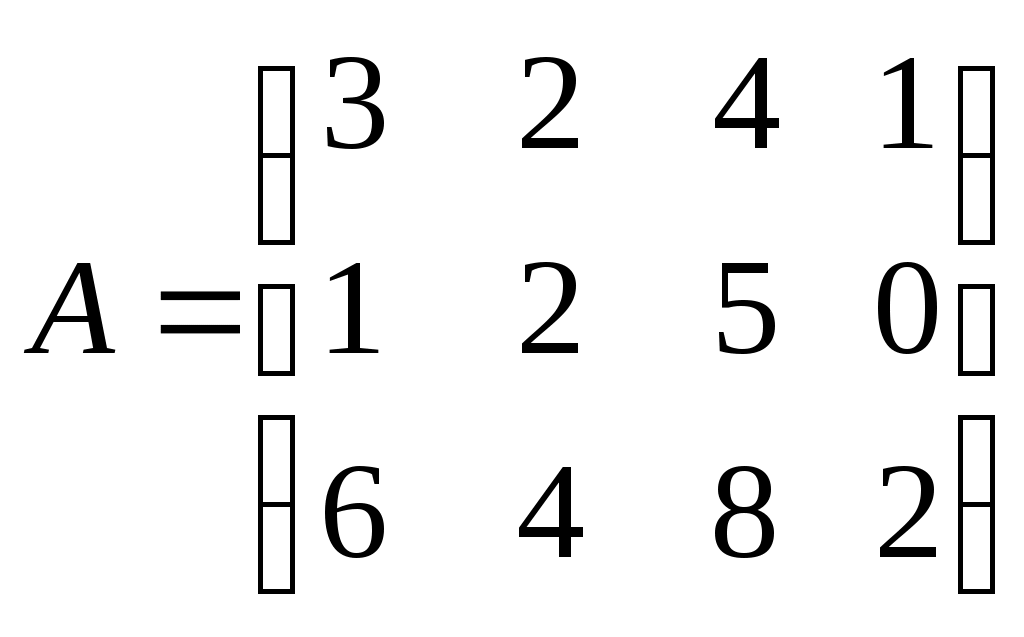равен

1. 0 2. 1 3. 2 4. 3

49. 
    
    

Для того, чтобы квадратная матрица А не имела обратную матрицу, необходимо и достаточно, чтобы

1. det A был отличен от 0

2.det A не существовал

3. det A был равен 0

4.det A был равен 1

50. 
    
    

Для того, чтобы возвести матрицу A в квадрат, нужно

1. Умножить матрицу A саму на себя , если это возможно

2.Возвести в квадрат элементы одной из строк матрицы

3.Возвести в квадрат элементы одного из столбцов матрицы

4. Каждый элемент матрицы возвести в квадрат

2 КАТЕГОРИЯ

51.

Матрица А имеет размерность и

1. 3 2. 4 3. 81 4.48

52.

.

Какое из разложений Δ на сумму двух определителей неверно:

1. 2.

3. 4.

53.

Какая сумма не существует?

1.A + B

2.

3.

4.

54.