Укажите неверное соотношение:
1. 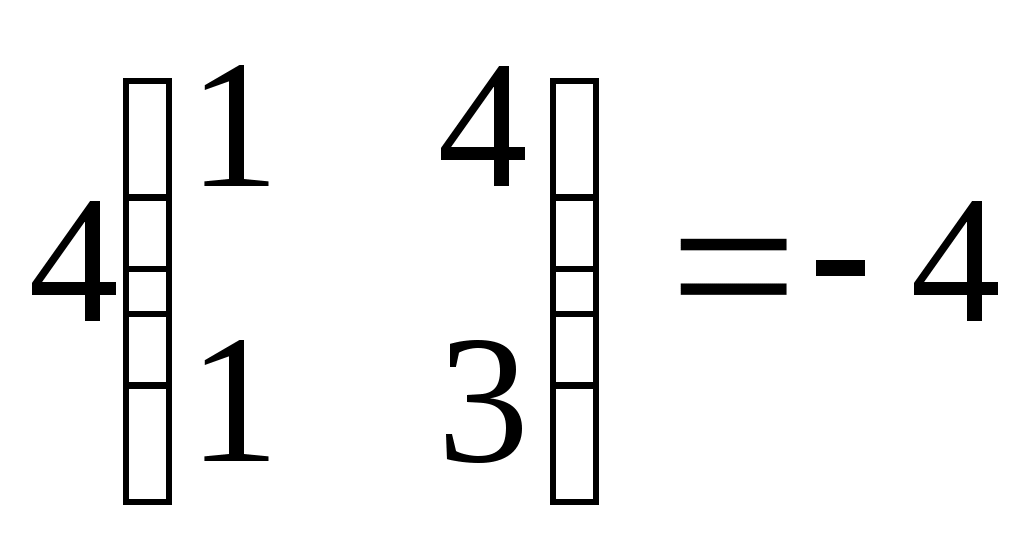 2. 2. 
3.  4. 4. 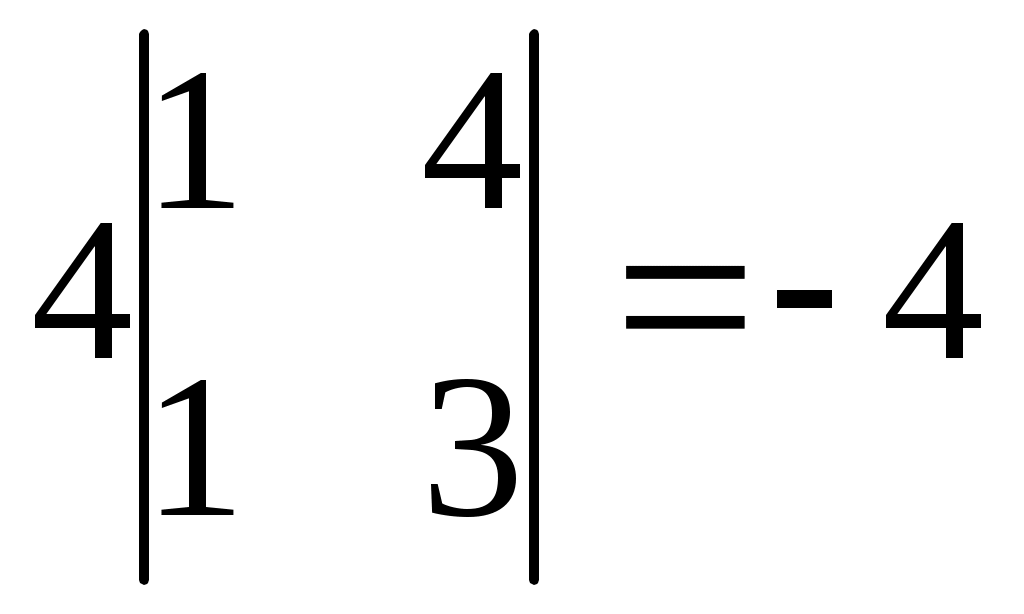
|
73.
| Для системы 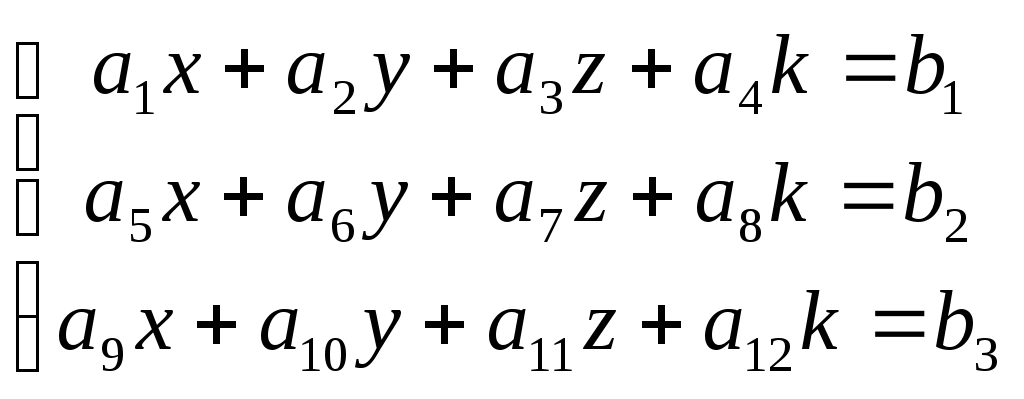 выполнено условие: r(A)=r(B)=3, где выполнено условие: r(A)=r(B)=3, где
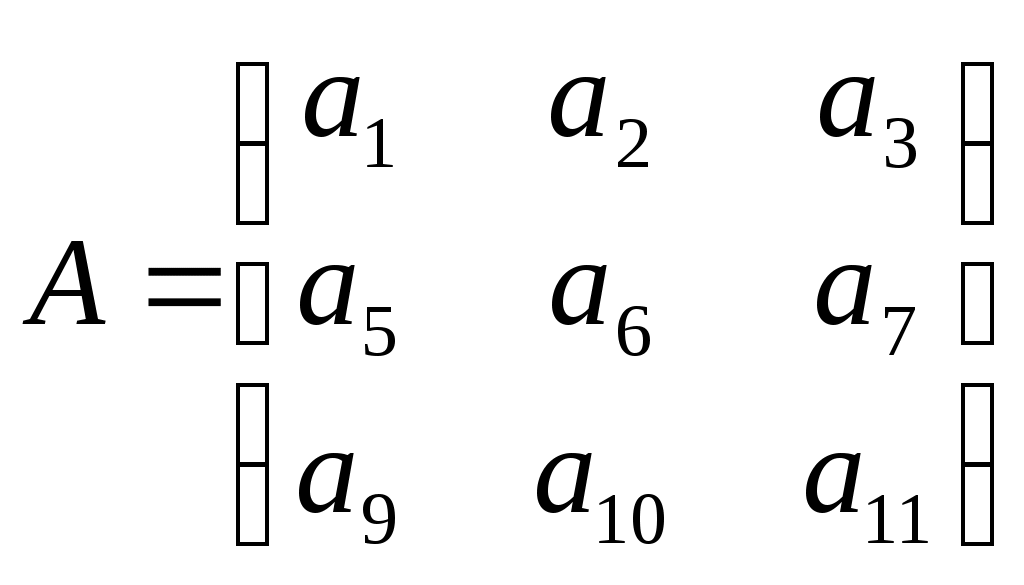 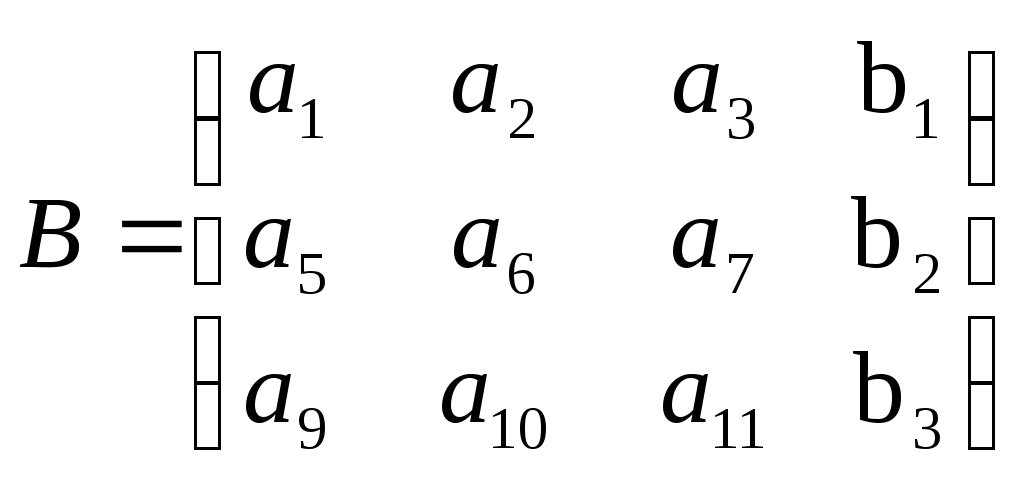 . Что можно сказать на основании этого? . Что можно сказать на основании этого?
|
Система имеет одно решение
Система имеет бесконечное множество решений
Система не имеет решений
Ничего определённого сказать нельзя
|
74.
|
Укажите верное соотношение (К=const)
|
1. 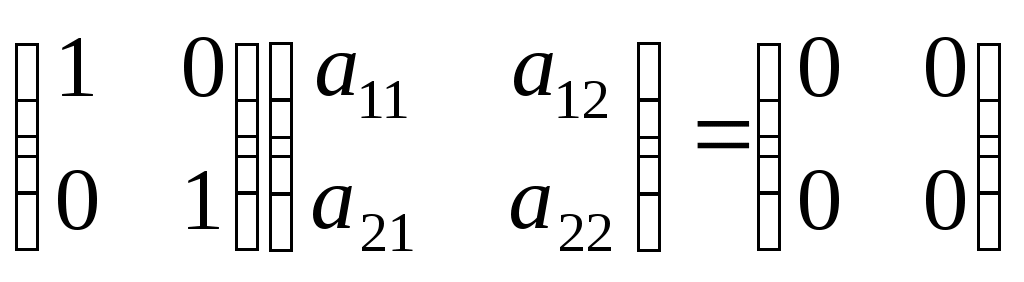
2. 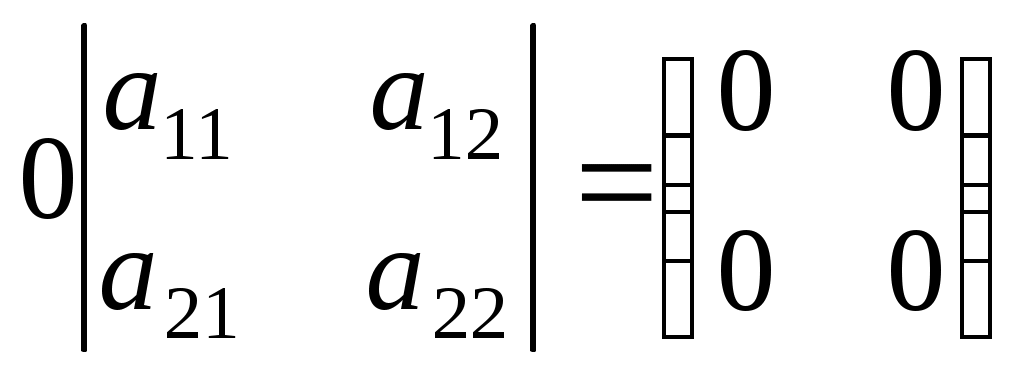
3. 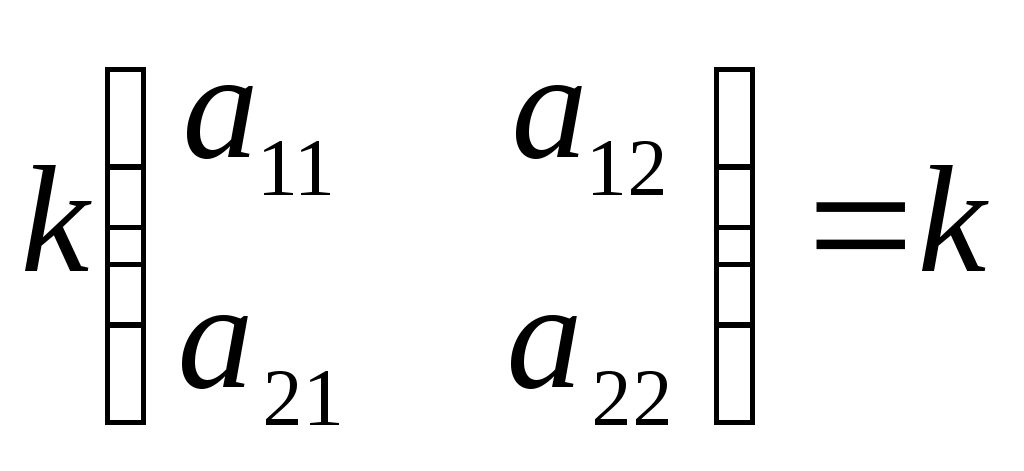
4. 
|
75.
|
После преобразований расширенная матрица системы линейных алгебраических уравнений имеет вид 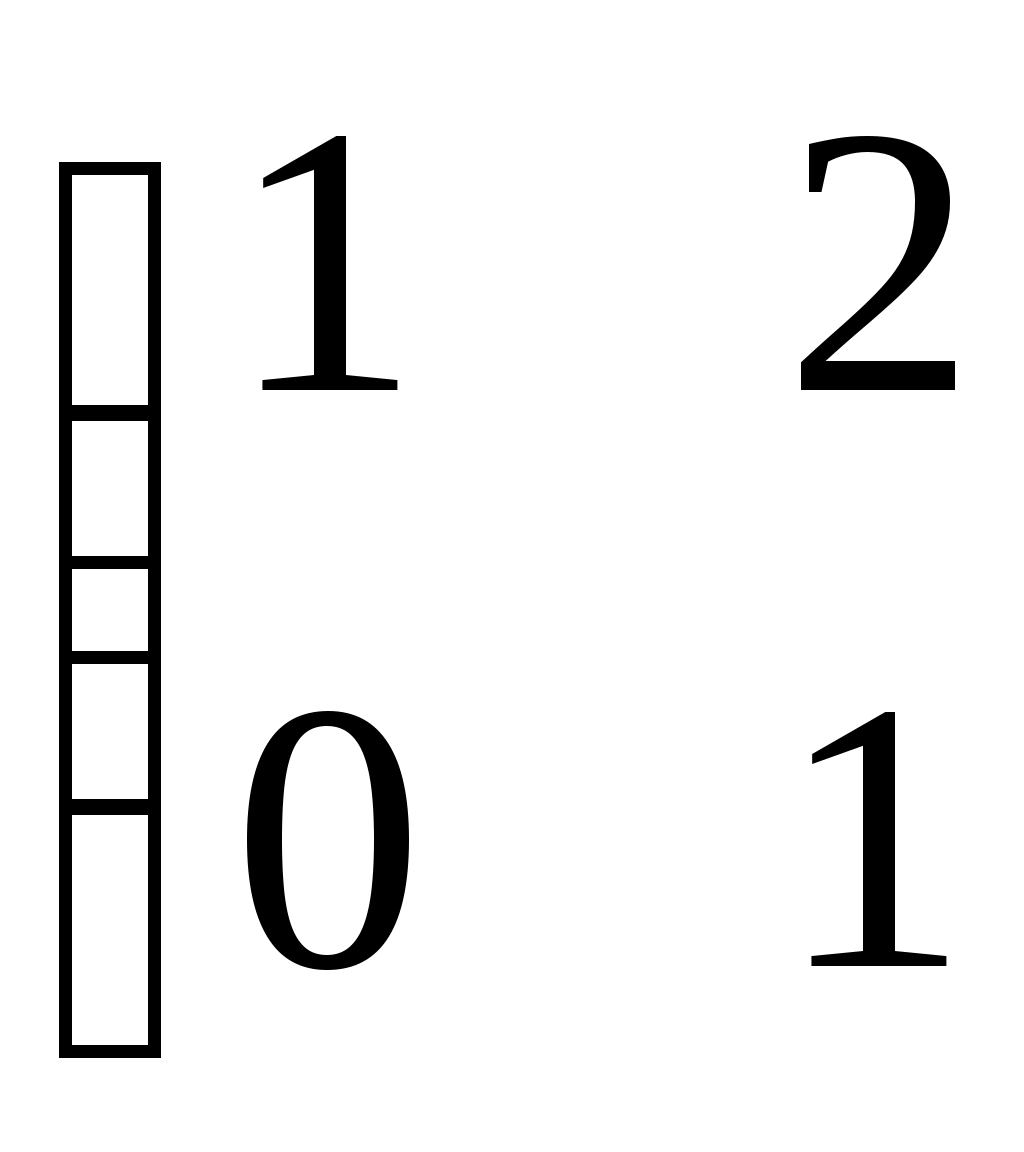 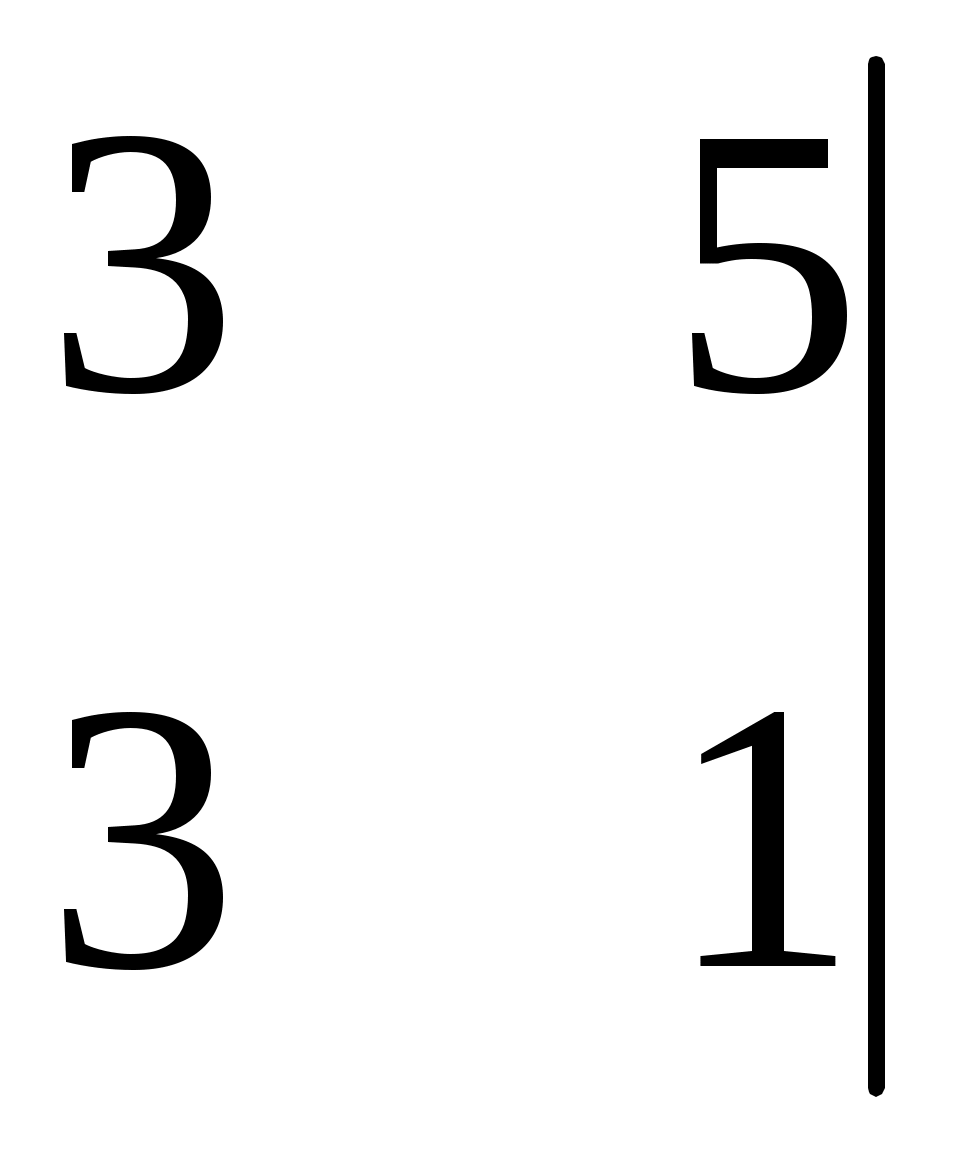 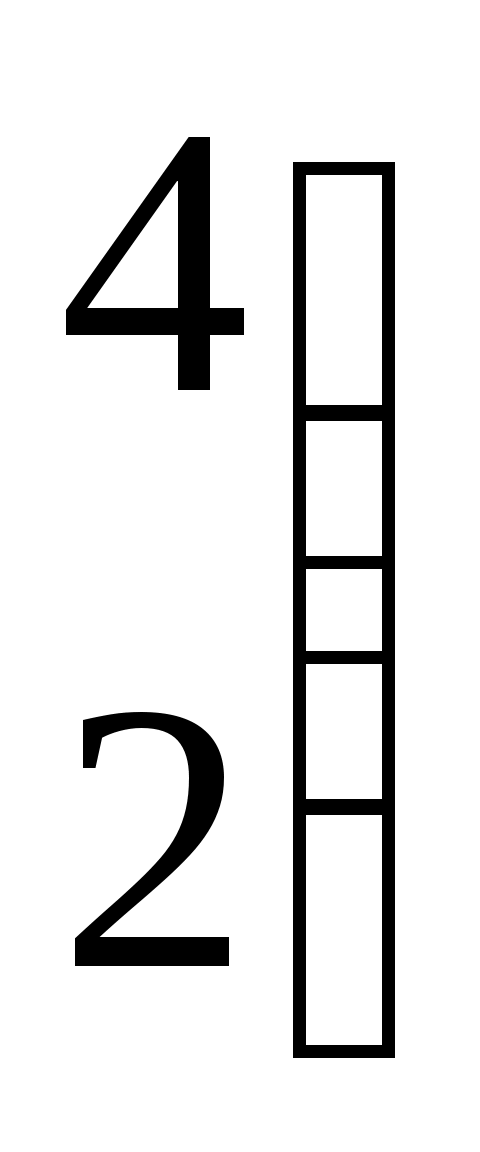 . Общее решение данной системы содержит: . Общее решение данной системы содержит:
|
1. 1 базисную неизвестную и 3 свободные
2. 2 базисные неизвестные и 2 свободные
3. 1 базисную неизвестную и 2 свободные
4. 3 базисные неизвестные и 1 свободную
|
76.
|
Система однородных линейных алгебраических уравнений всегда имеет решения, отличные от нулевого, если в ней
|
1.количество уравнений равно количеству неизвестных
2.количество уравнений больше количества неизвестных
3.количество уравнений меньше количества неизвестных
4.любая система однородных линейных алгебраических уравнений имеет решения, отличные от нулевого
|
77.
| Пусть определитель квадратной матрицы размерности kXk равен нулю. Что можно сказать про ранг этой матрицы? |
он равен нулю
он равен k
он больше k
он меньше k
|
78.
|
Какие из перечисленных пар матриц не всегда будут перестановочными?
|
1.произвольная матрица A и её транспонированная матрица 
2.две диагональные матрицы одной размерности
3.невырожденная квадратная матрица A и её обратная матрица 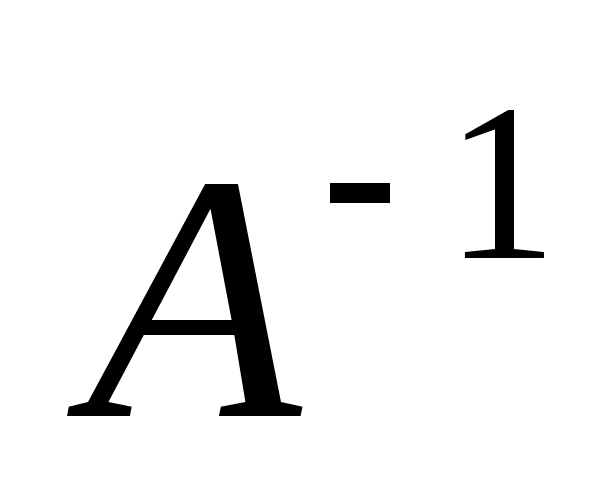
4.две единичные матрицы одной размерности
|
79.
| | 1. 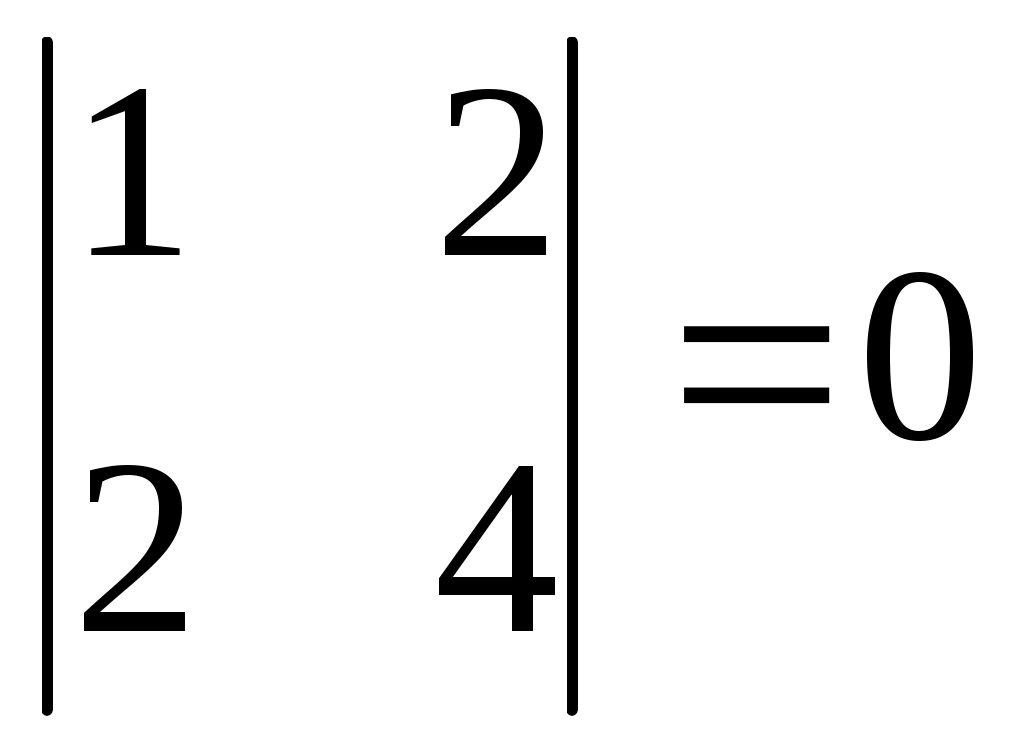 2. 2. 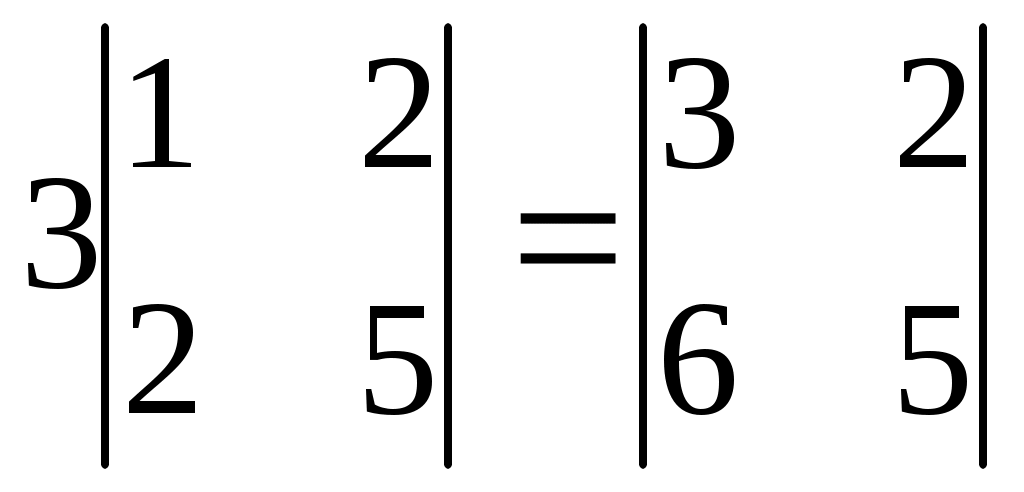
3.  4. 4. 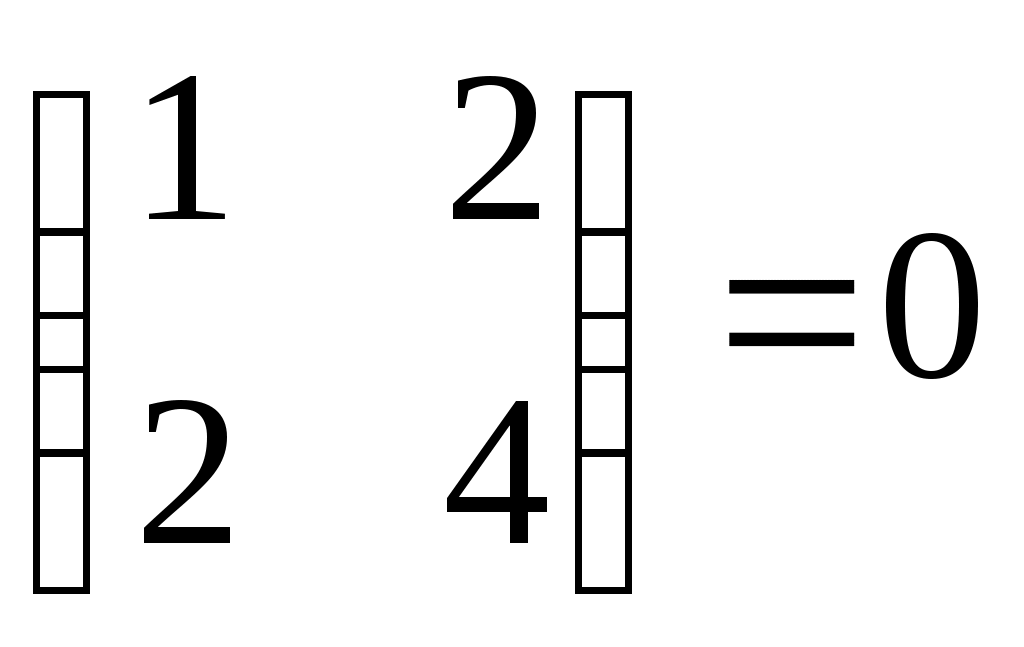
|
80.
| Пусть 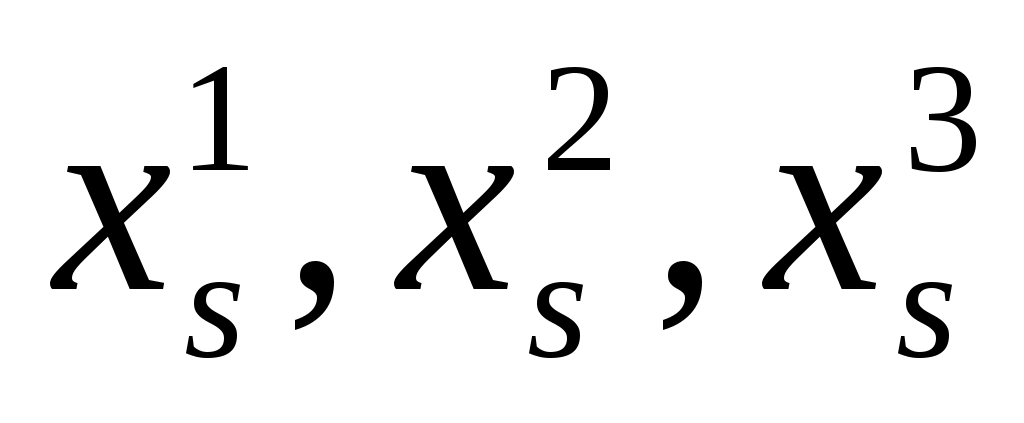 - решения системы однородных линейных алгебраических уравнений. Тогда решением этой системы будет выражение - решения системы однородных линейных алгебраических уравнений. Тогда решением этой системы будет выражение |
1. 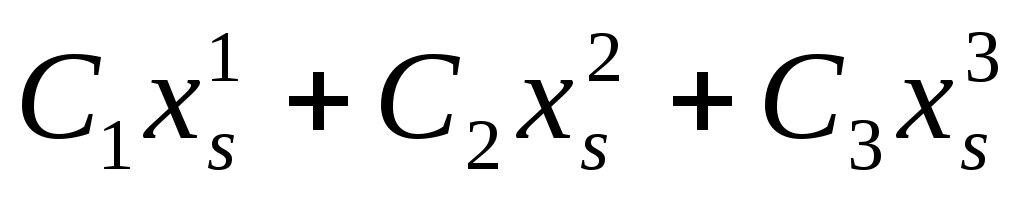
2. 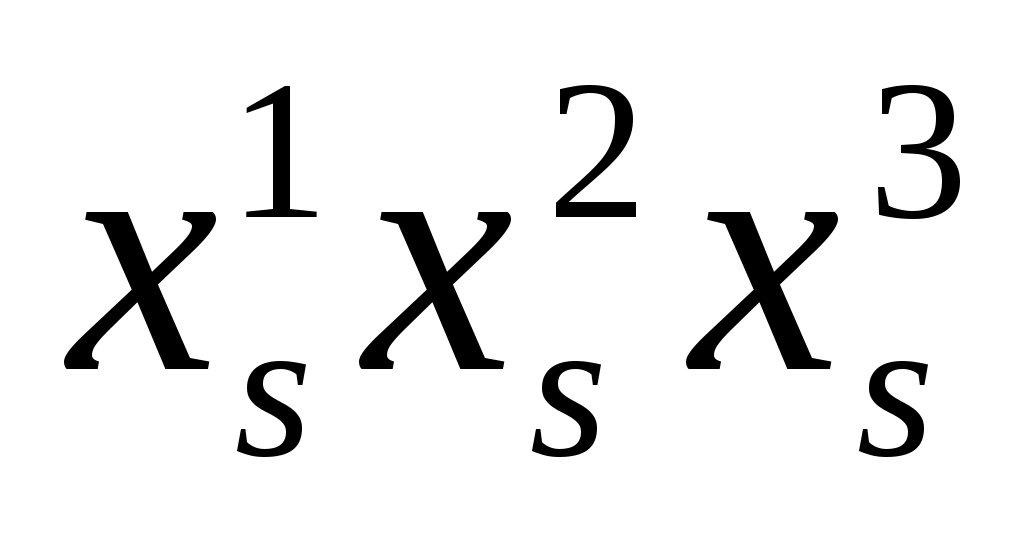
3. 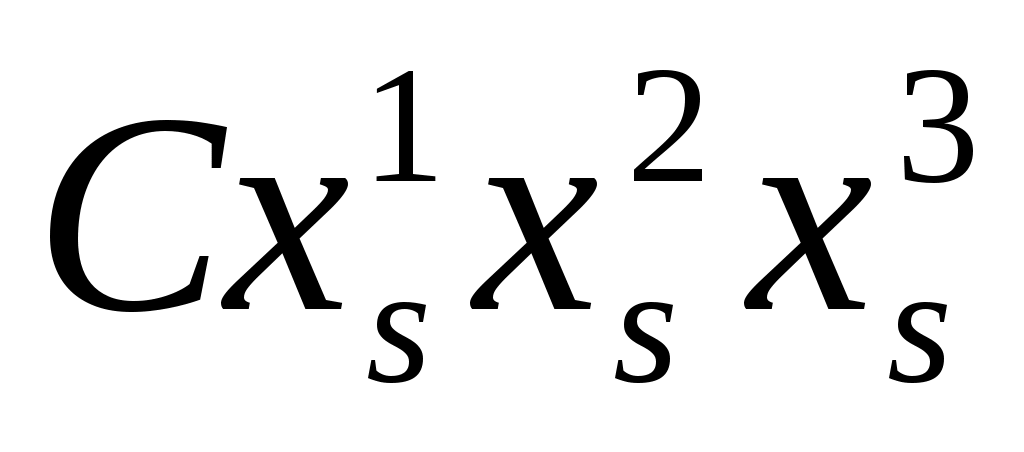
4. 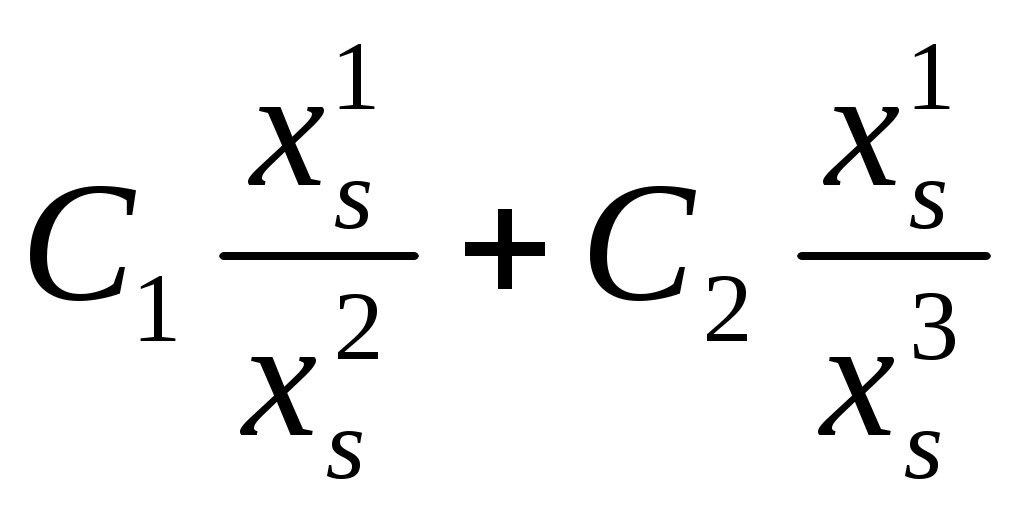 ( (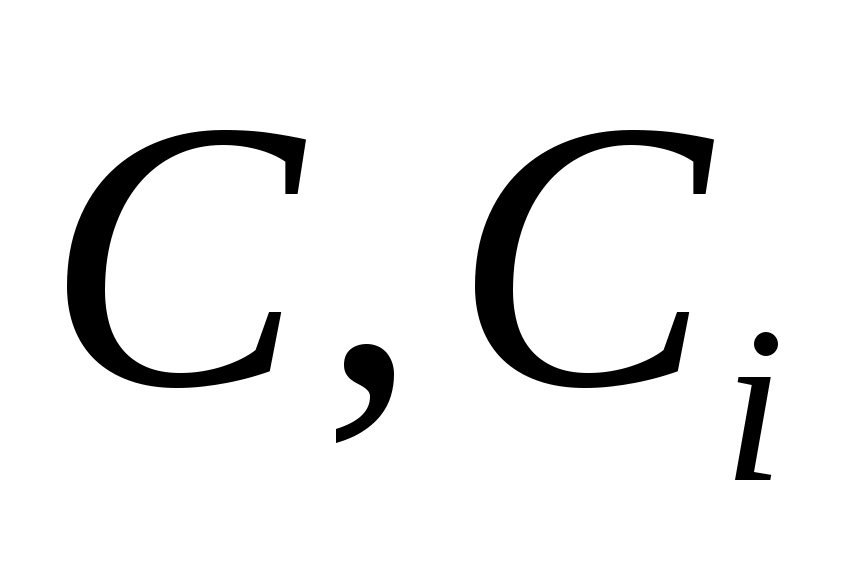 - const) - const)
|
81.
|
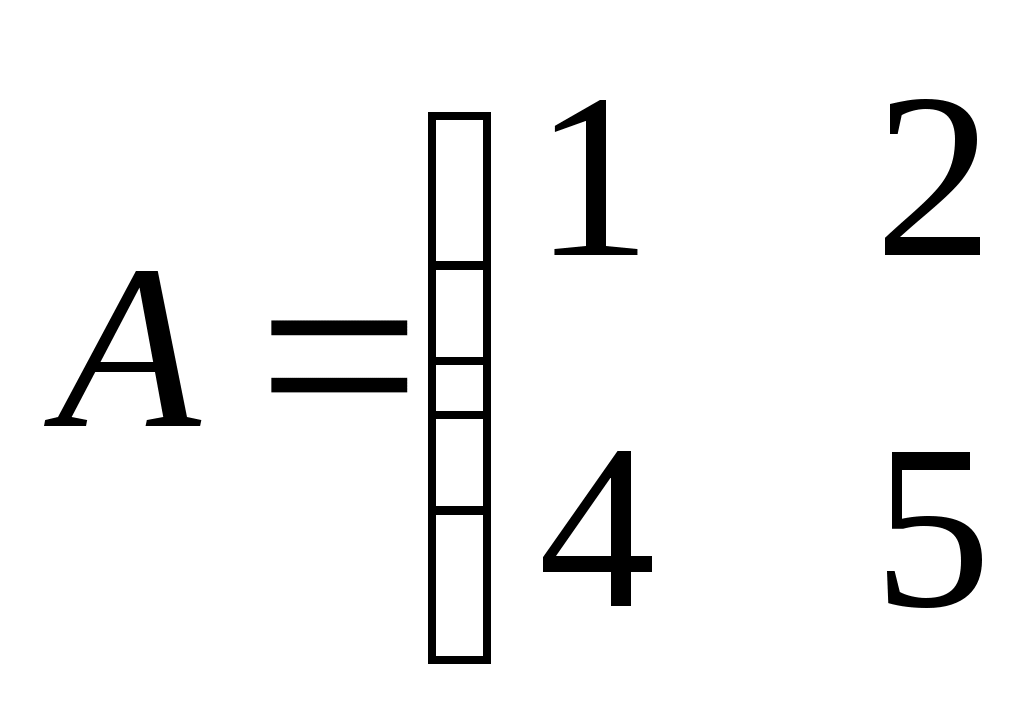 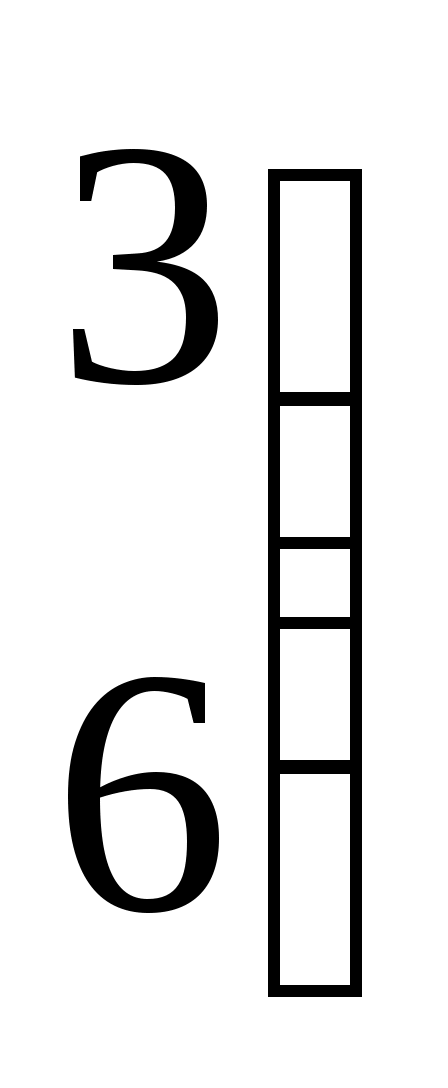 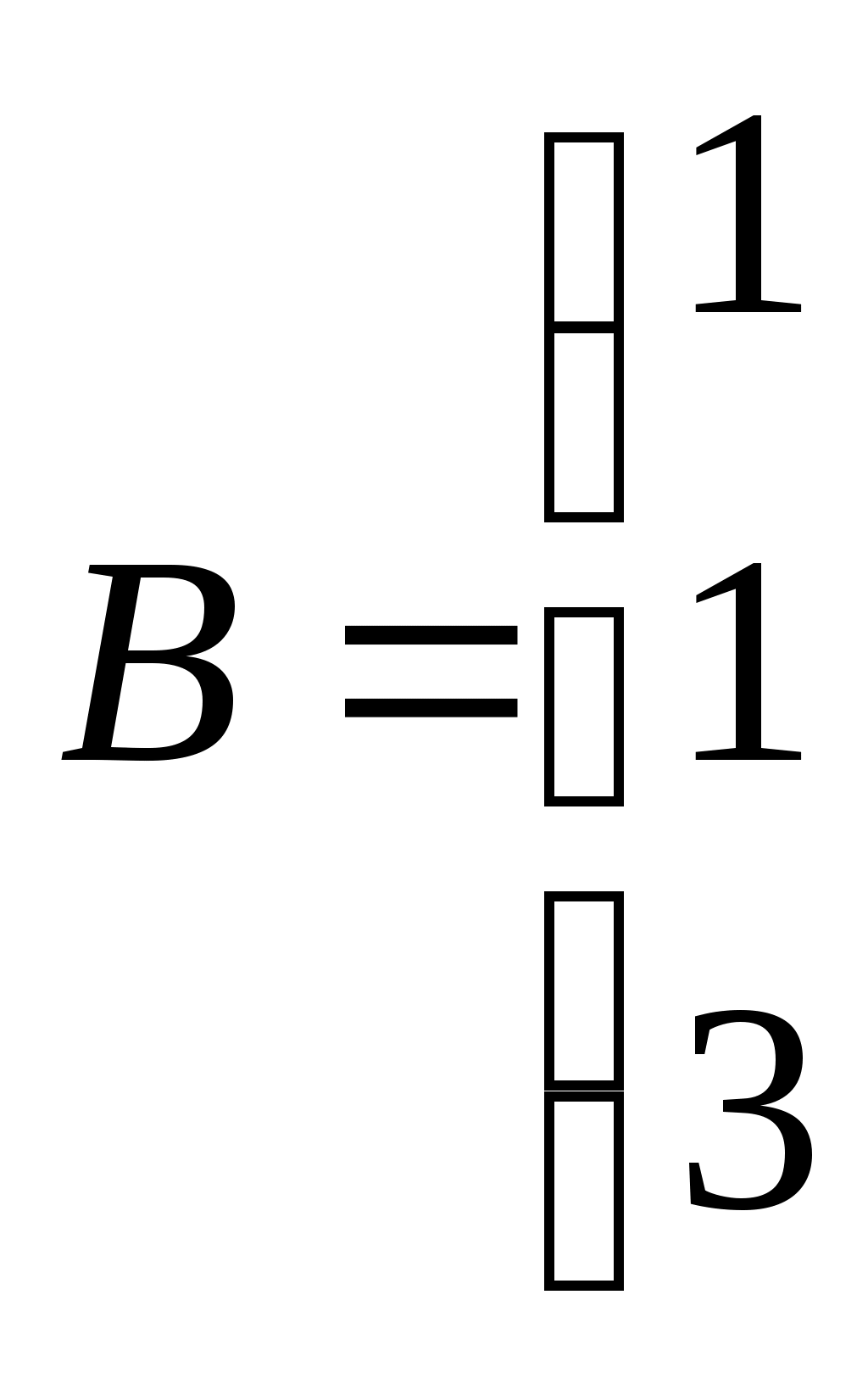  Какая операция невозможна? Какая операция невозможна?
|
1. AB 2.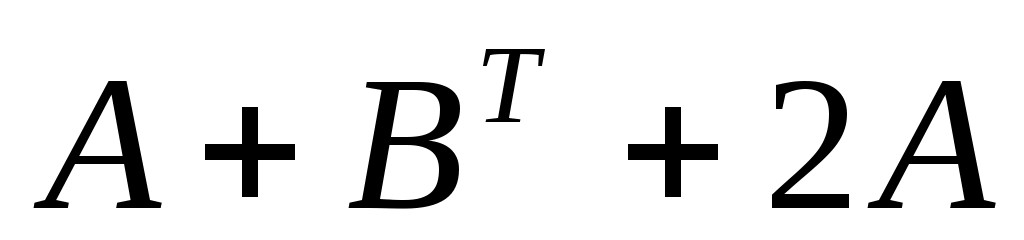 3. 3. 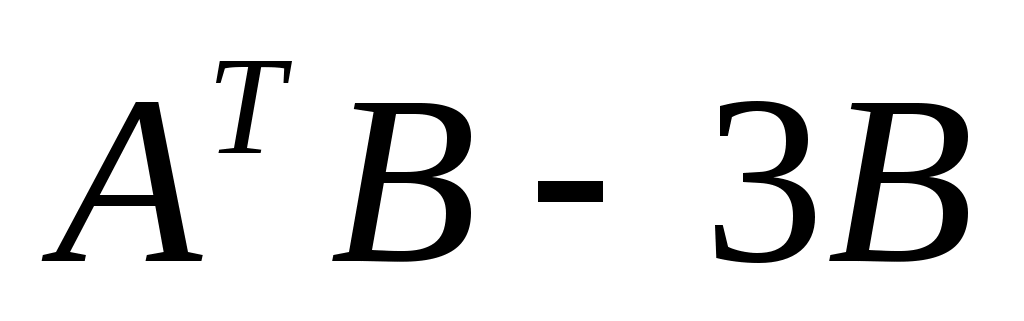 4. BA 4. BA
|
82.
|
Пусть все миноры порядка k определителя n-го порядка (k |
1.определитель равен нулю
2.все миноры порядка (k-1) определителя равны нулю
3.все элементы определителя равны 0
4.все миноры порядка (k+1) определителя равны нулю
|
83.
| 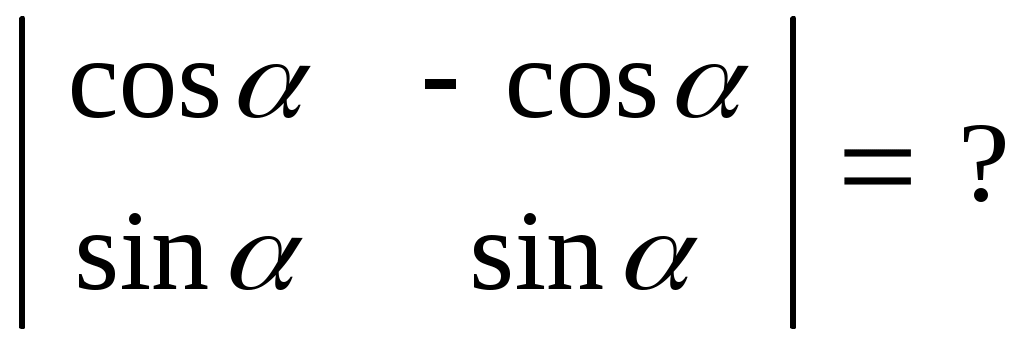
| 1. 0 2. 1 3. 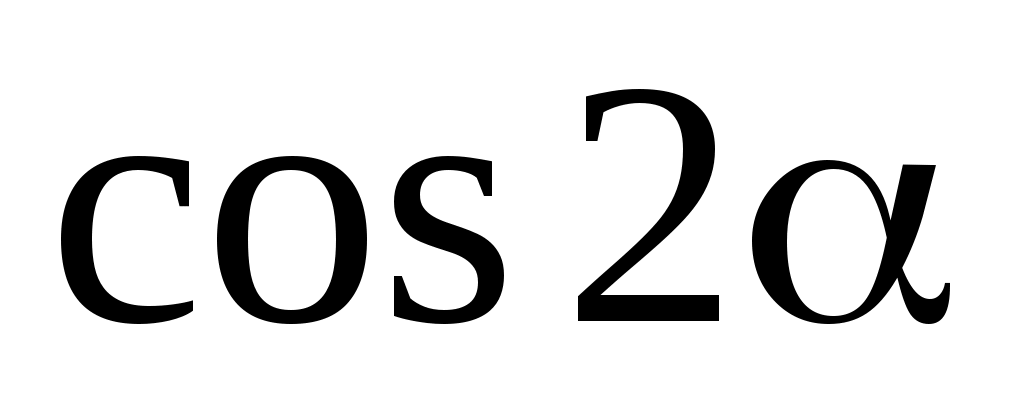  4. 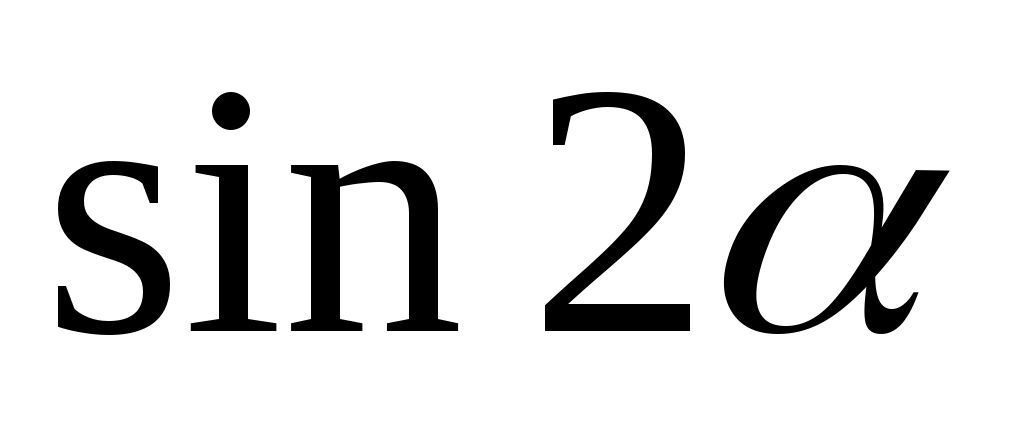 |
84.
| Сколько базисных и сколько свободных неизвестных содержит общее решение системы, если ее расширенная матрица после преобразований имеет вид: 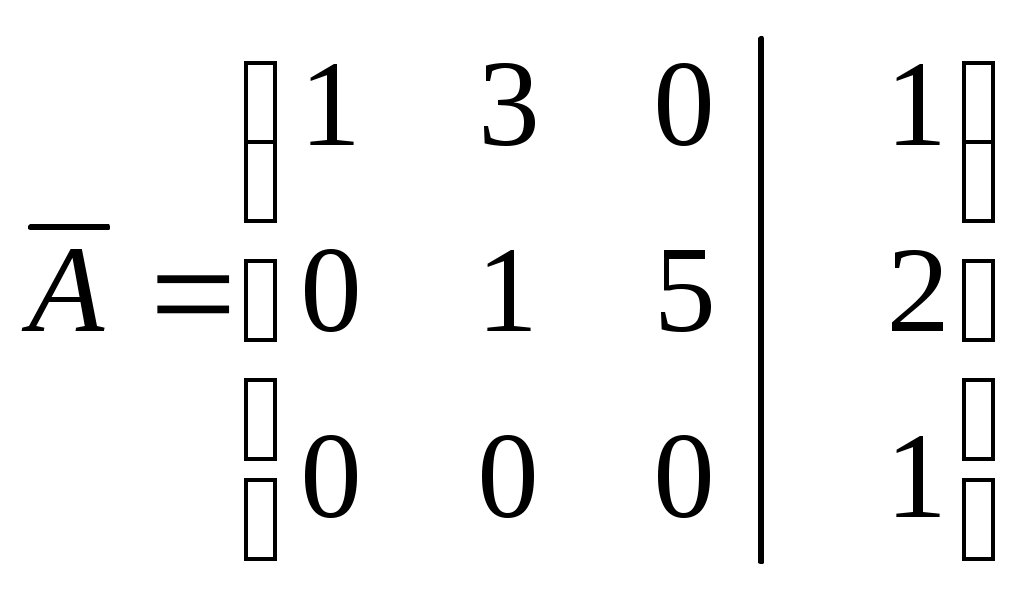 ? ?
|
Две базисные и одну свободную
Система не имеет решений
Одну базисную и две свободные
Все неизвестные в данной системе базисные
|
85.
| При каком значении х  = 0 ? = 0 ? |
2
0
1
-1
|
86.
| 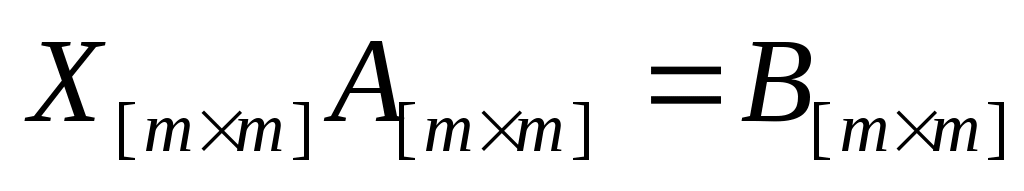 . .
Х = ? |
1.  2. 2. 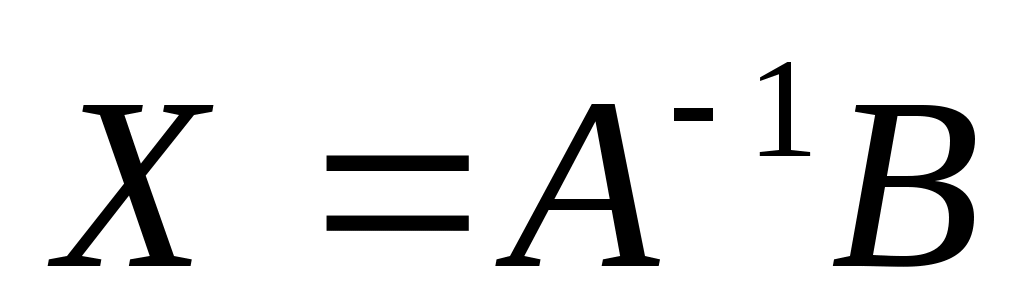 3. 3. 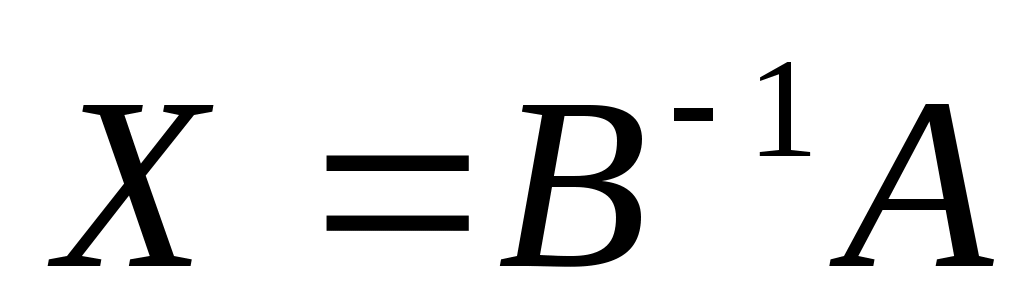
4. 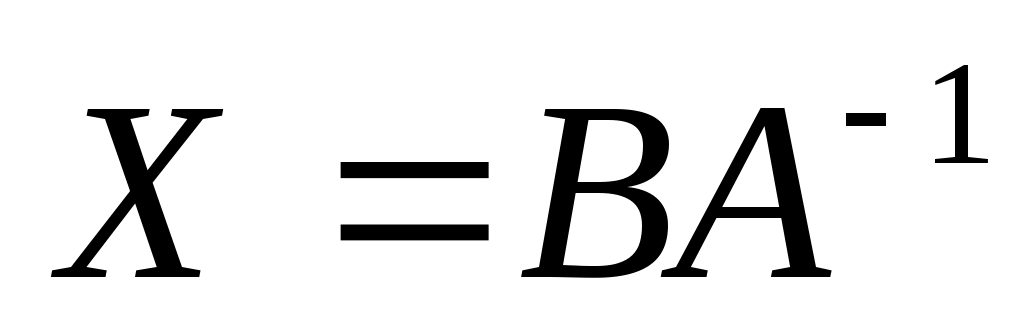
|
87.
| 
|
1. 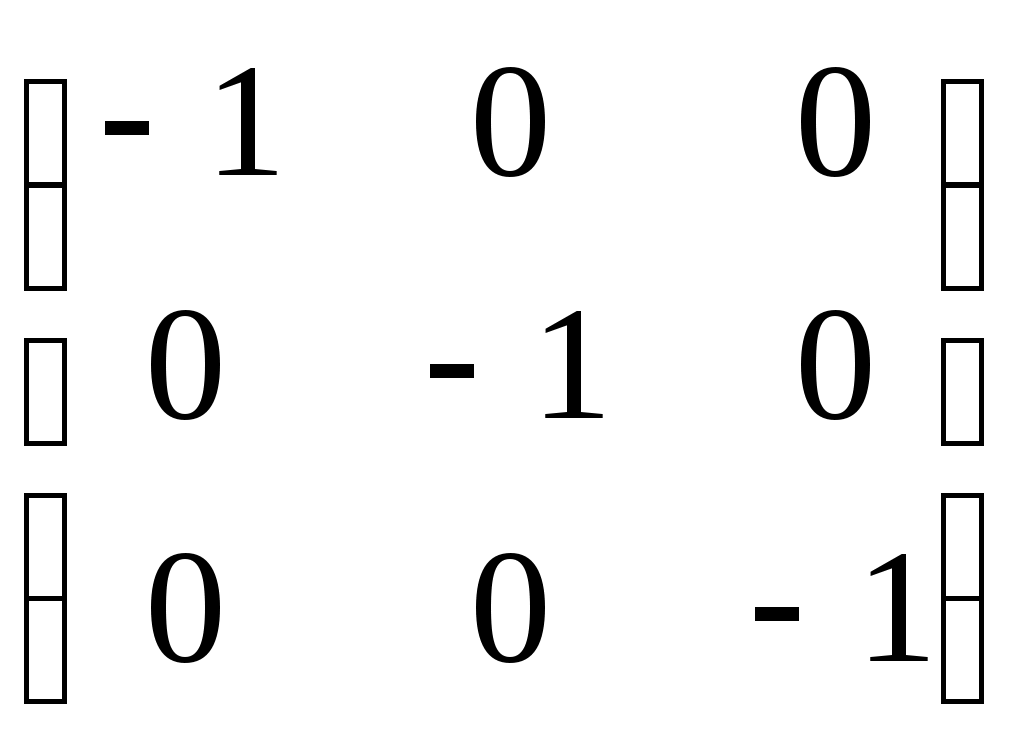 2. 2. 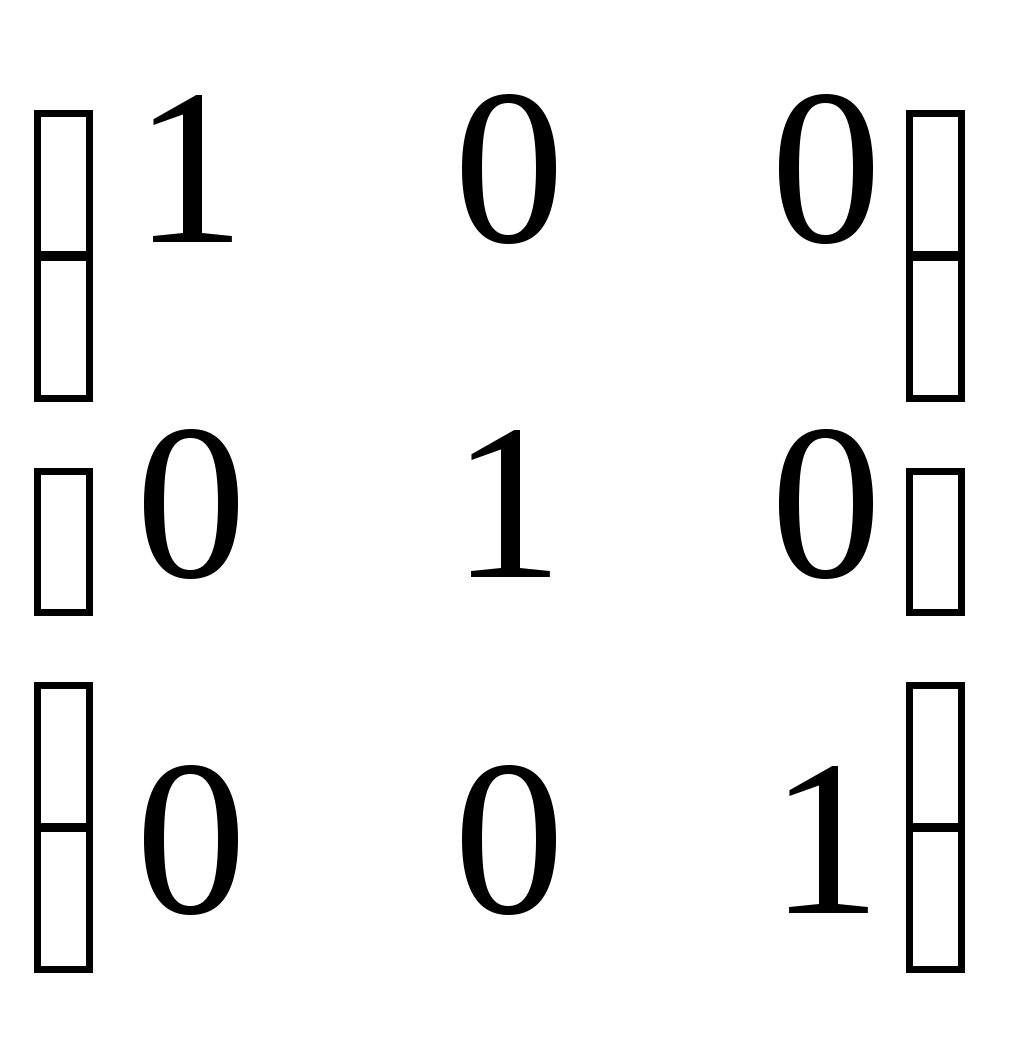
3.  4. 4. 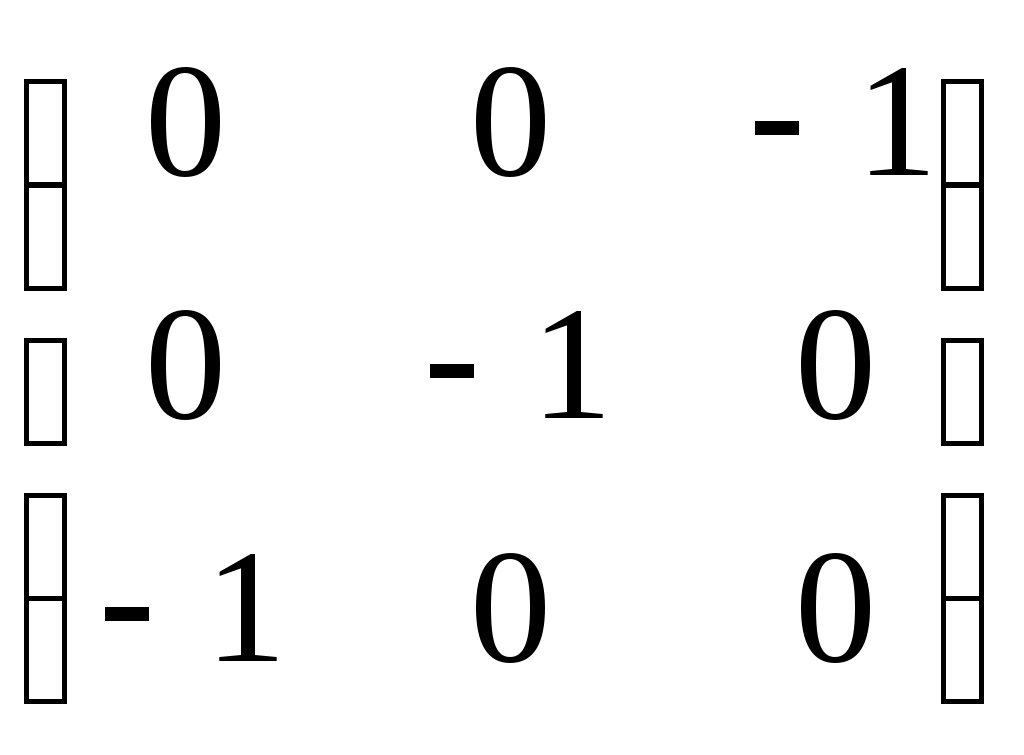
|
88.
|
Укажите неверное утверждение
|
1.В матрице количество строк может не совпадать с количеством столбцов
2.В матрице количество строк может совпадать с количеством столбцов
3.В определителе количество строк может не совпадать с количеством столбцов
4.В определителе квадратной матрицы всегда есть главная диагональ
|
89.
|
Укажите неверное свойство для квадратных матриц A,B и C одинаковой размерности
|
1. (A+B)+C=A+(B+C) 2. A(BC)=(AB)C
3. (A+B)C=AC+BC 4. C(A+B)=AC+CB
|
90.
| Укажите неверное в общем случае утверждение |
1.Умножение матрицы любой размерности на соответствующую единичную матрицу не меняет матрицу
2. Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу
3. При сложении квадратной матрицы любого порядка с соответствующей единичной матрицей её элементы, стоящие на главной диагонали, увеличиваются на 1
4. Сложение матрицы любой размерности с соответствующей нулевой матрицей не меняет матрицу
|
91.
|
Укажите верное утверждение для системы
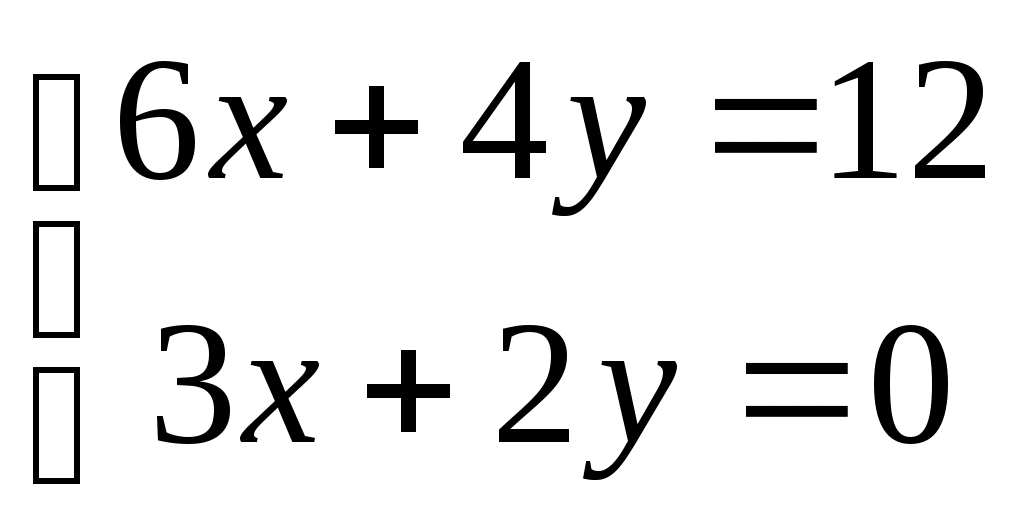
|
1.Система имеет единственное решение
2. 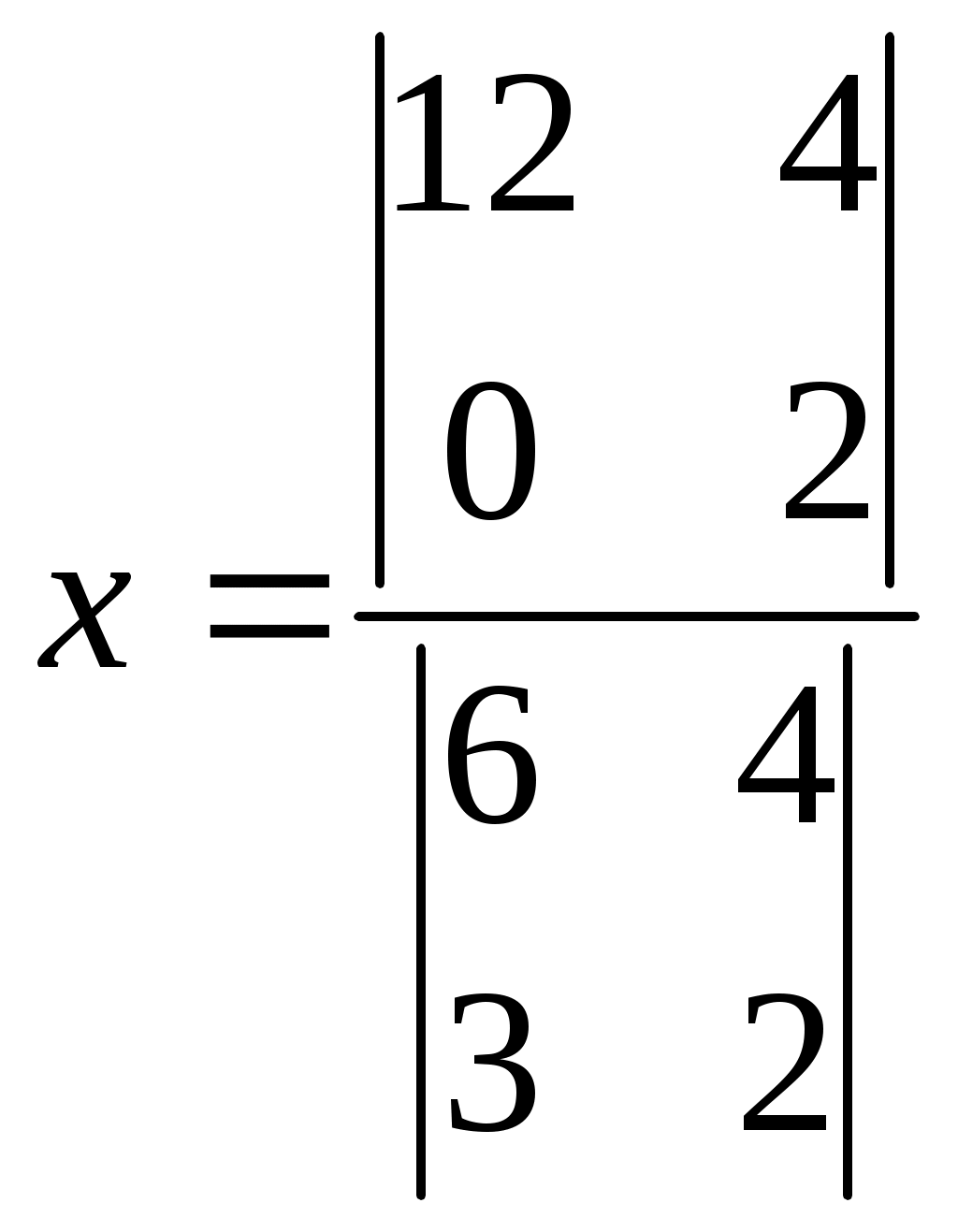 3. 3. 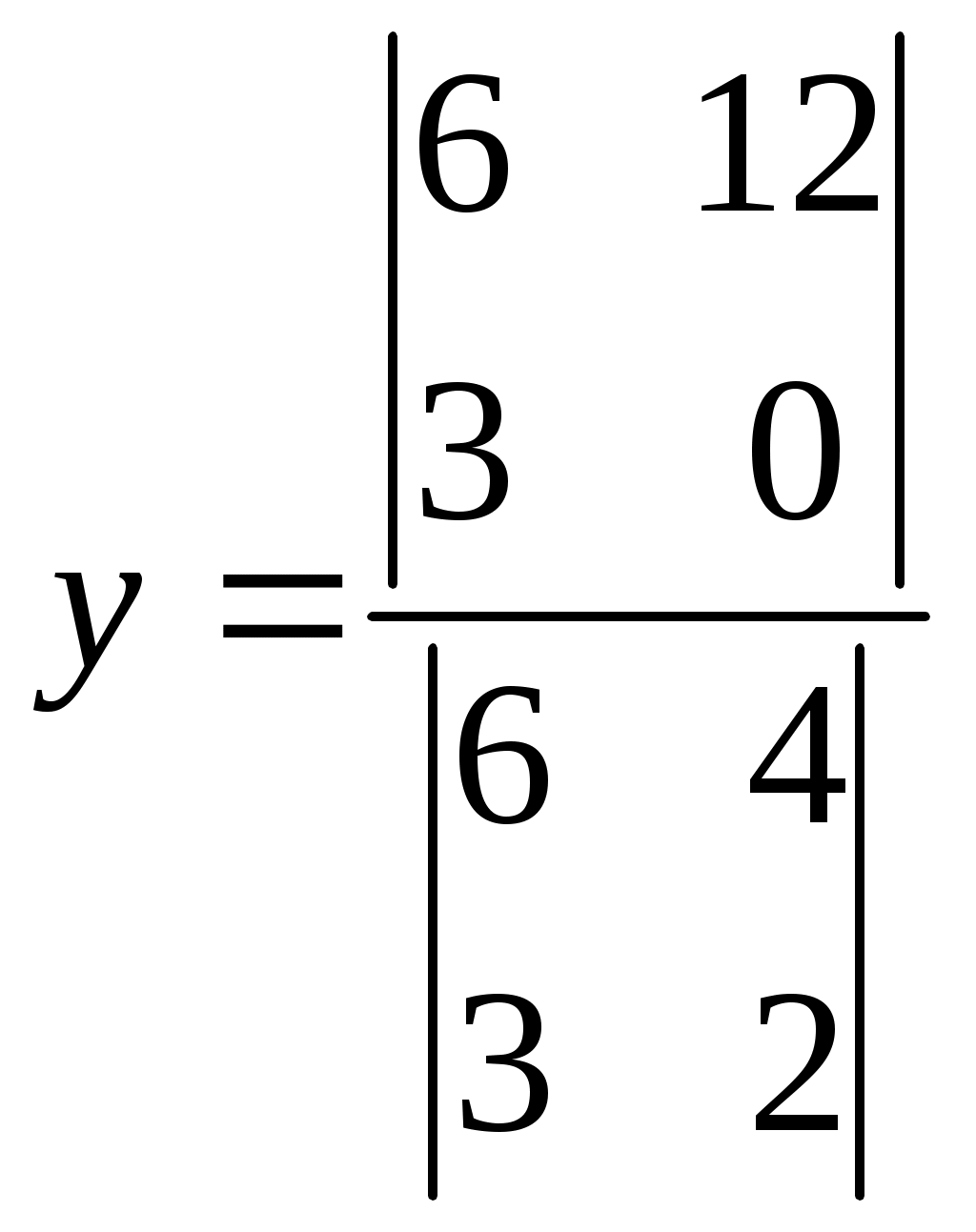
4. У системы не может быть единственного решения
|
92.
|
Какая из перечисленных систем может не иметь решений?
|
1.  2. 2. 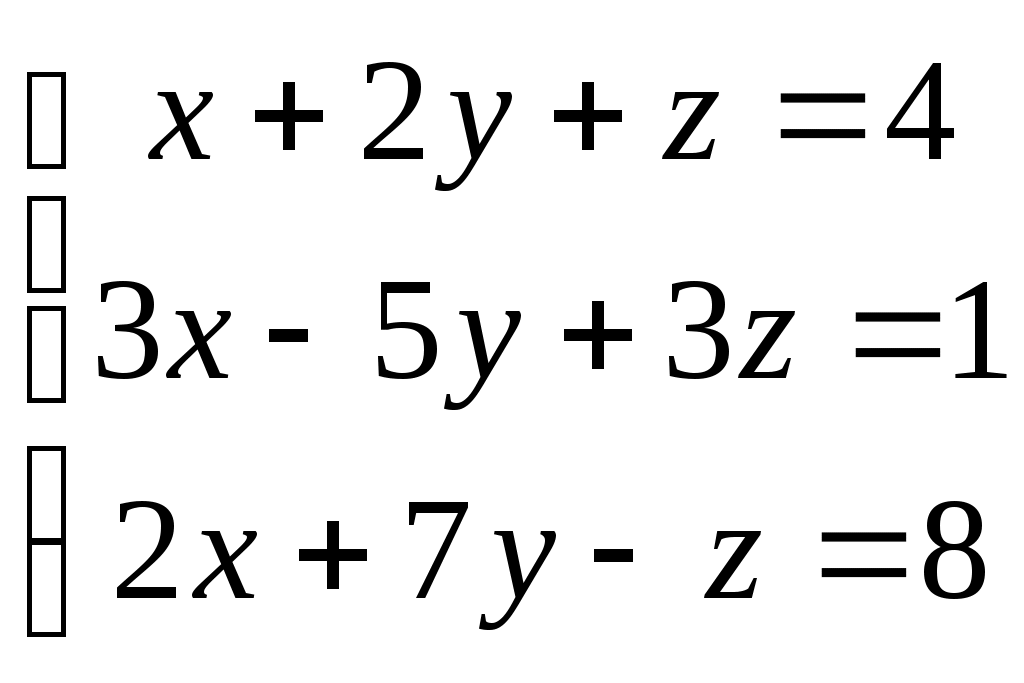
3. 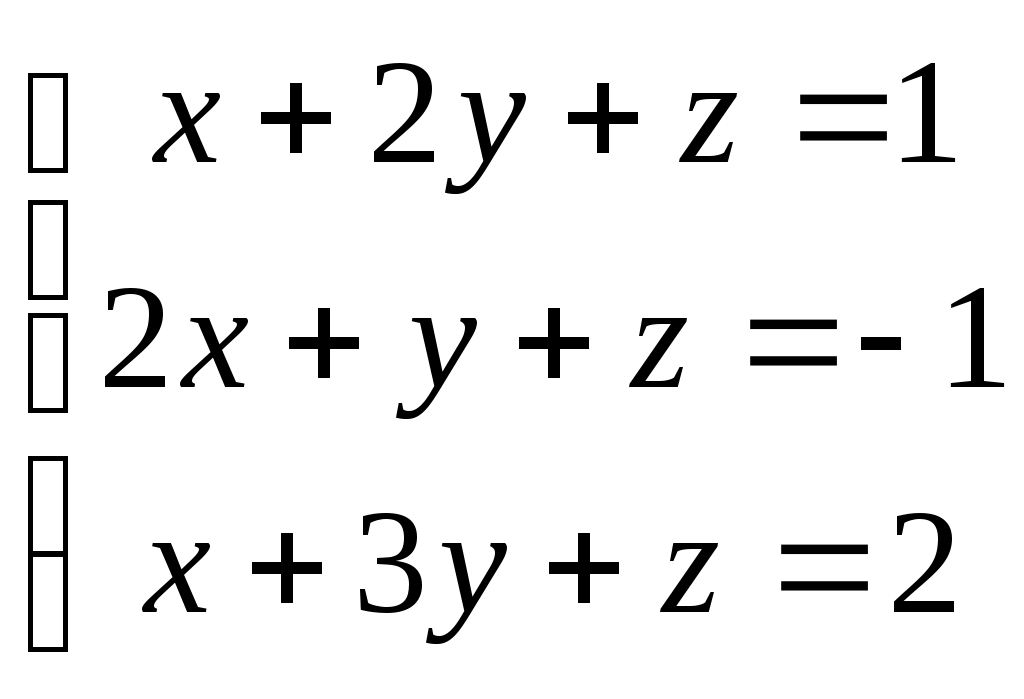 4. 4. 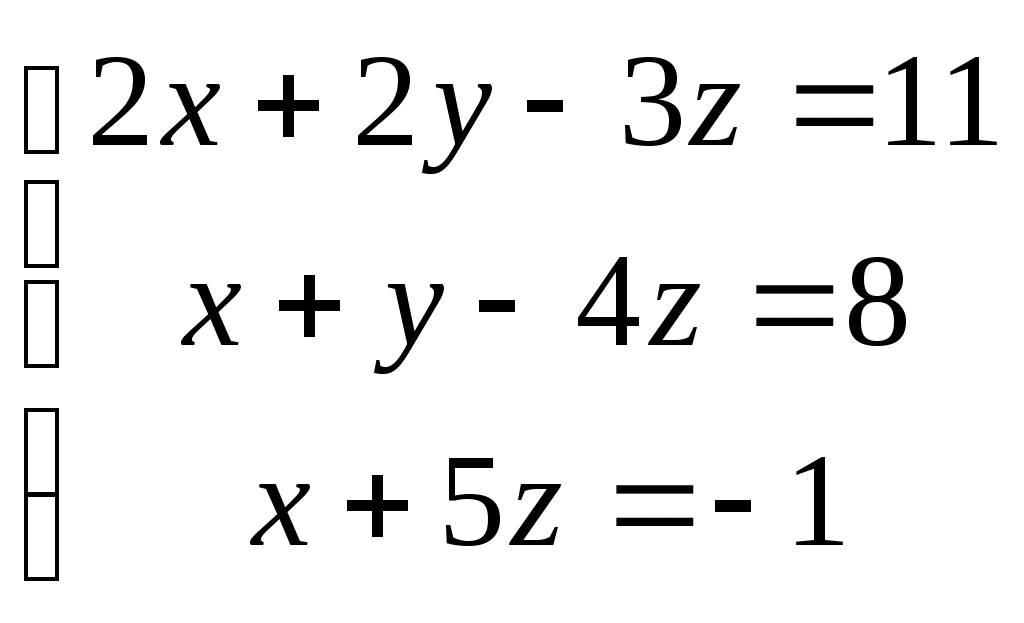
|
93.
|
Укажите симметрическую матрицу
|
1.  2. 2. 
3. 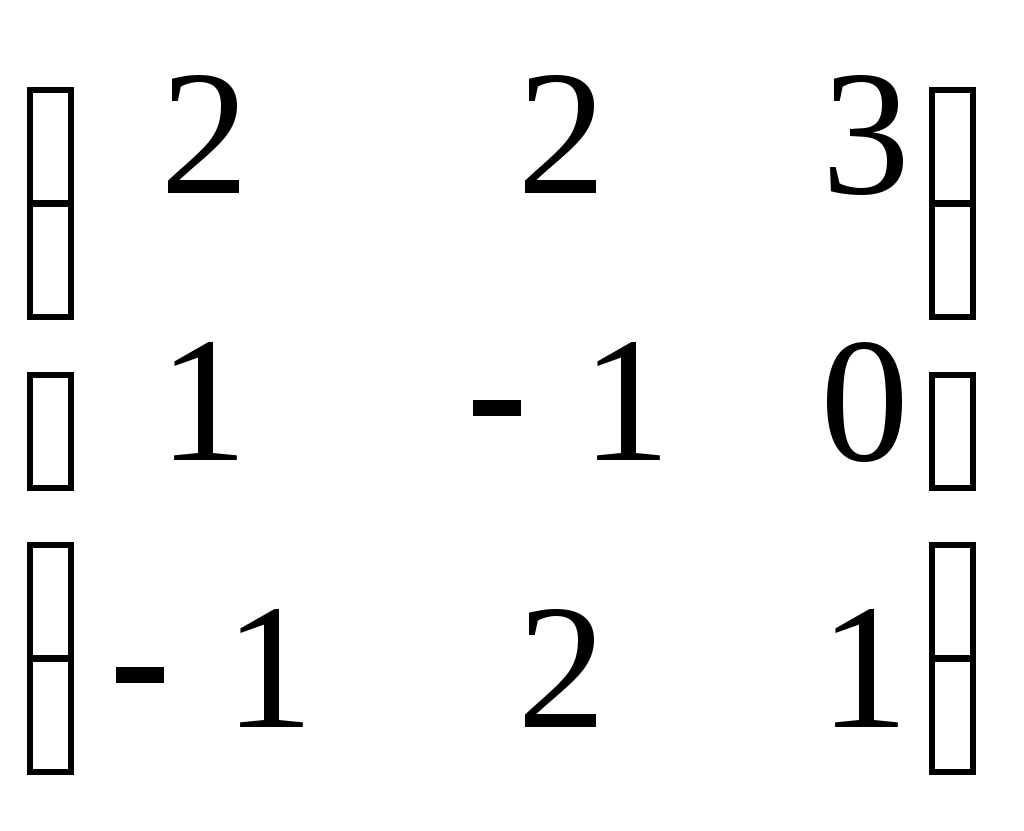 4. 4. 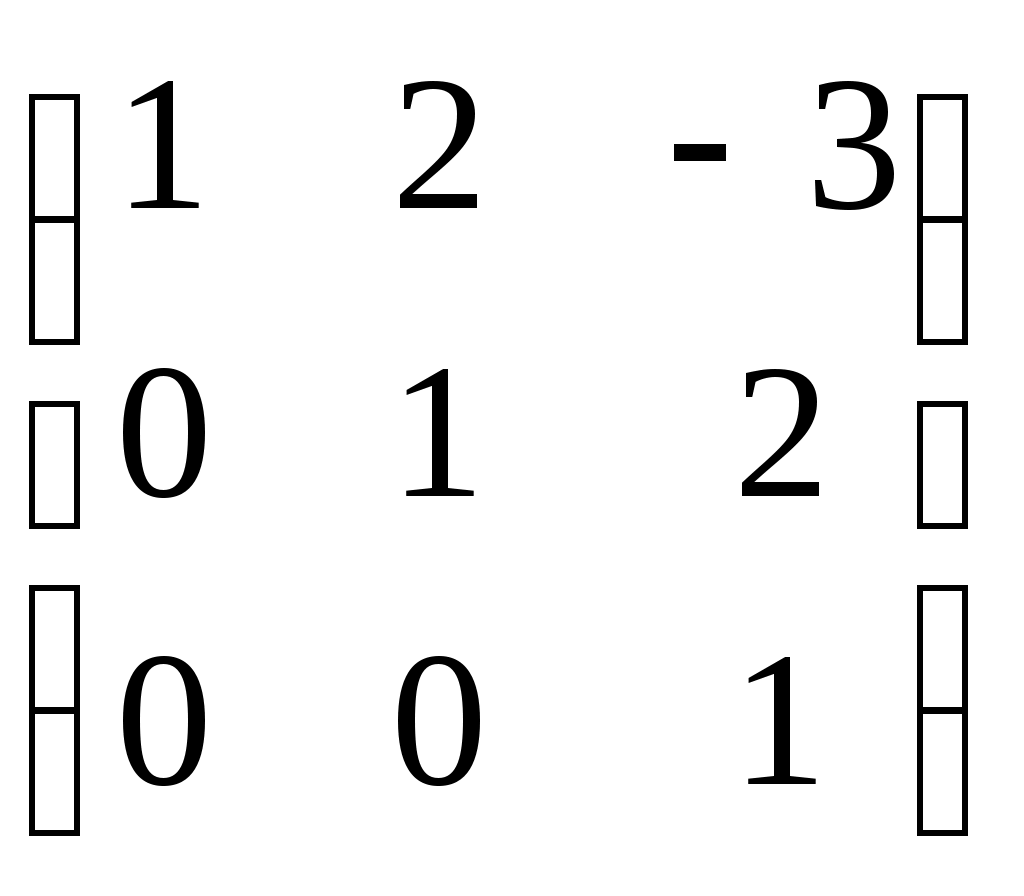
|
94.
| Какая из перечисленных матриц может не быть симметрической? |
1. диагональная 2. единичная
3. квадратная нулевая 4. нулевая
|
95.
|
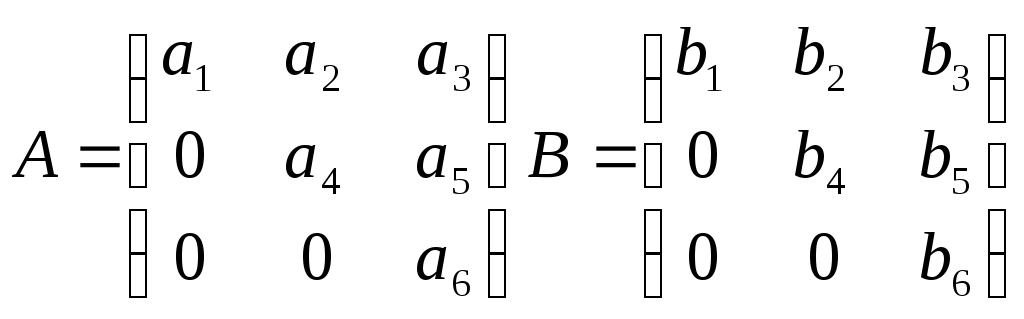 Какое утверждение в общем случае неверно? Какое утверждение в общем случае неверно?
|
1.AB – верхняя треугольная матрица
2.BA - верхняя треугольная матрица
3. AB – верхняя треугольная матрица и AB=BA
4. AB – верхняя треугольная матрица и 
|
96.
| Какое утверждение в общем случае неверно? |
1.Если A – симметрическая матрица, то 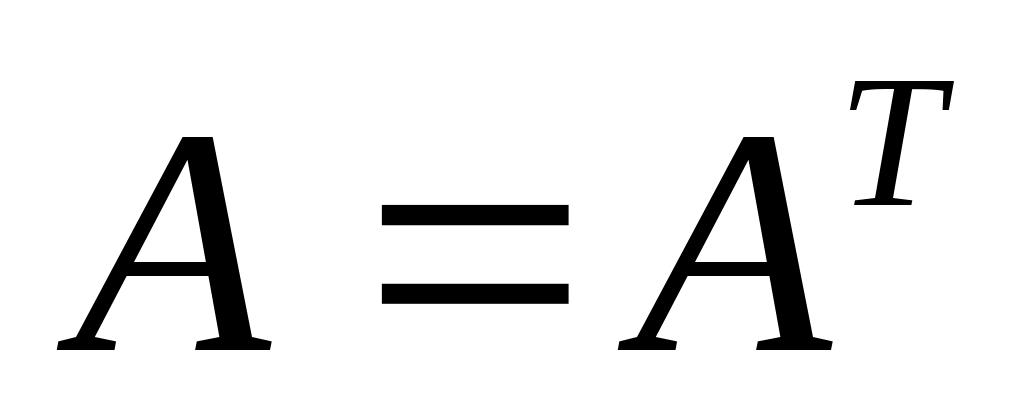
2. Если A – кососимметрическая матрица, то 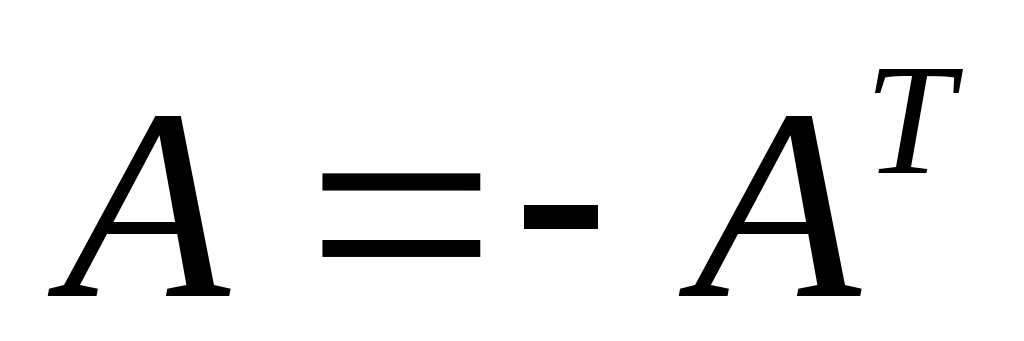
3. Если A и B – симметрические матрицы, то AB – симметрическая матрица
4. . Если A и B – симметрические матрицы, то AB – не обязательно симметрическая матрица
|
97.
|
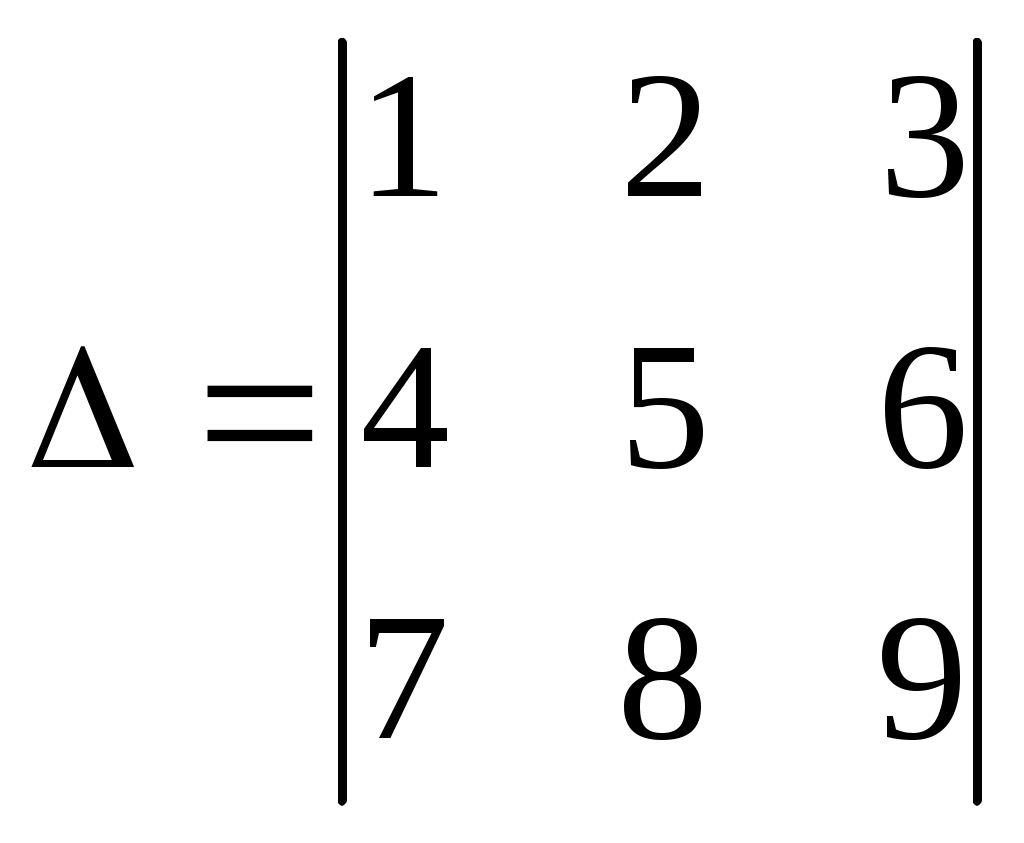 Какое равенство верно? Какое равенство верно?
|
1. 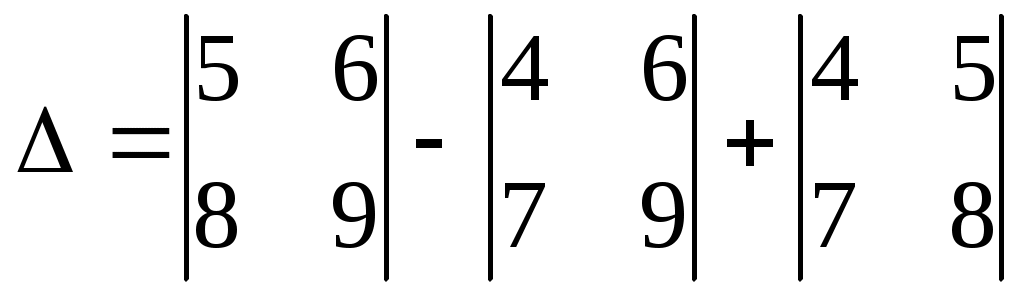
2. 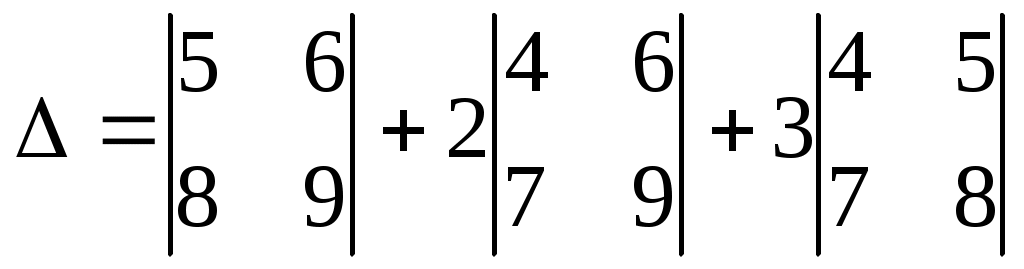
3. 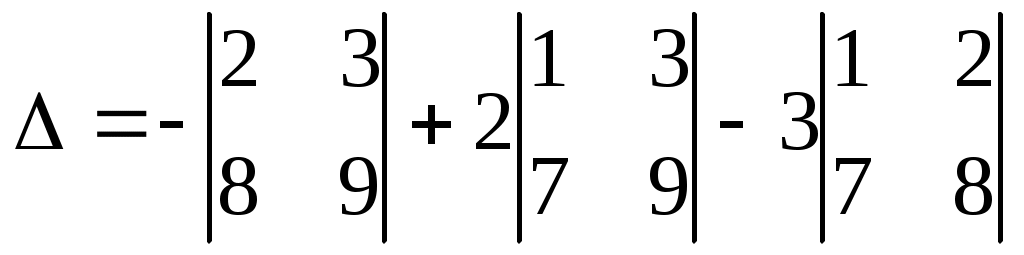
4. 
|
98.
|
Дан определитель 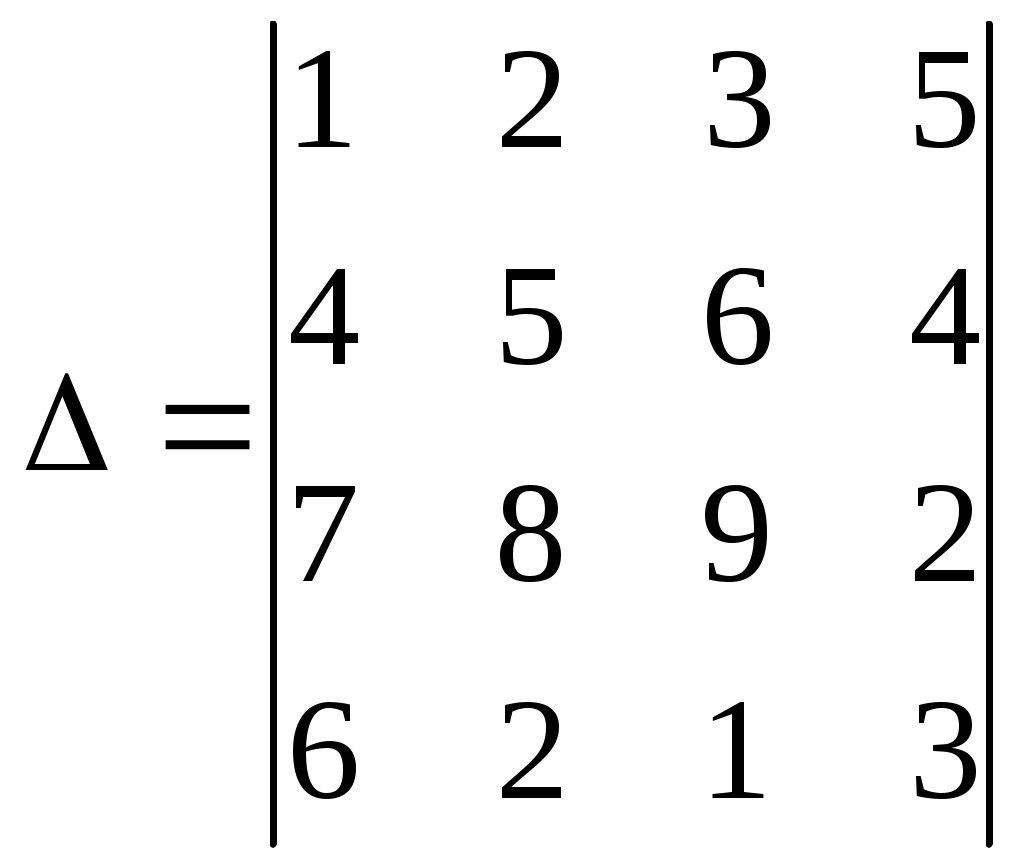 . Тогда . Тогда 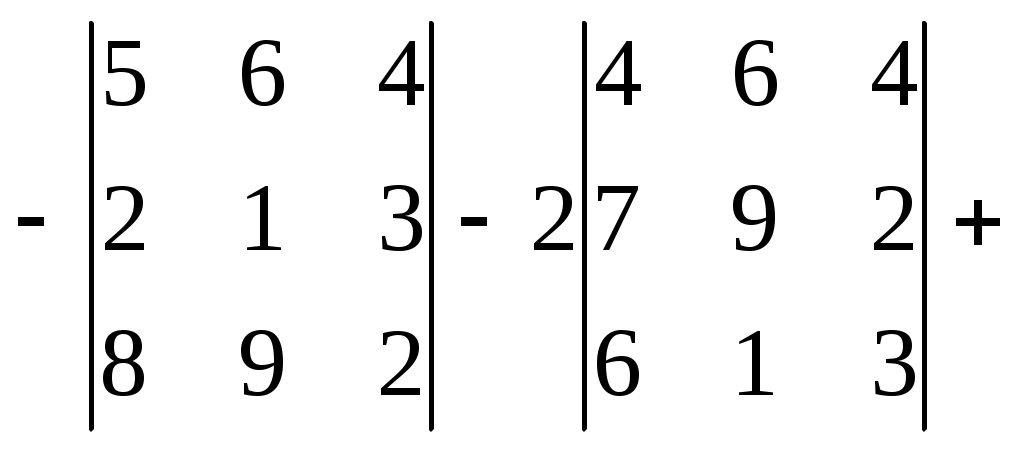
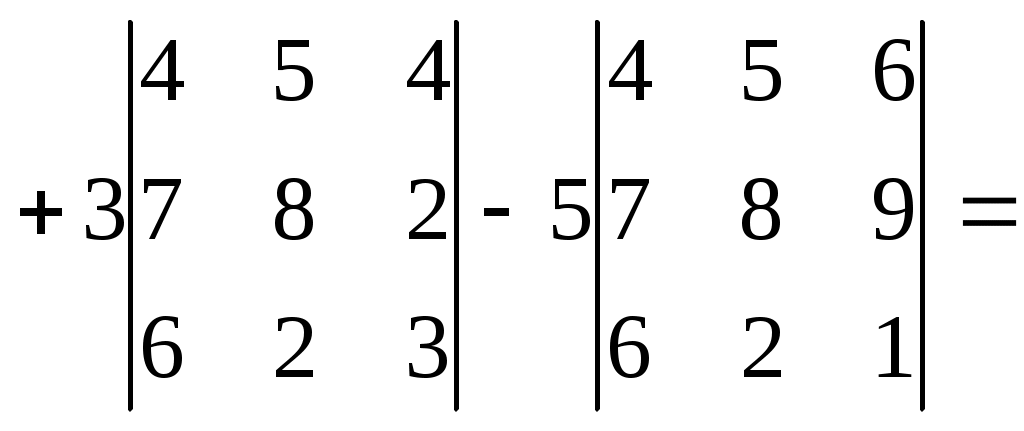
|
1. 0 2. 1 3.  4. 3 4. 3
|
99.
| 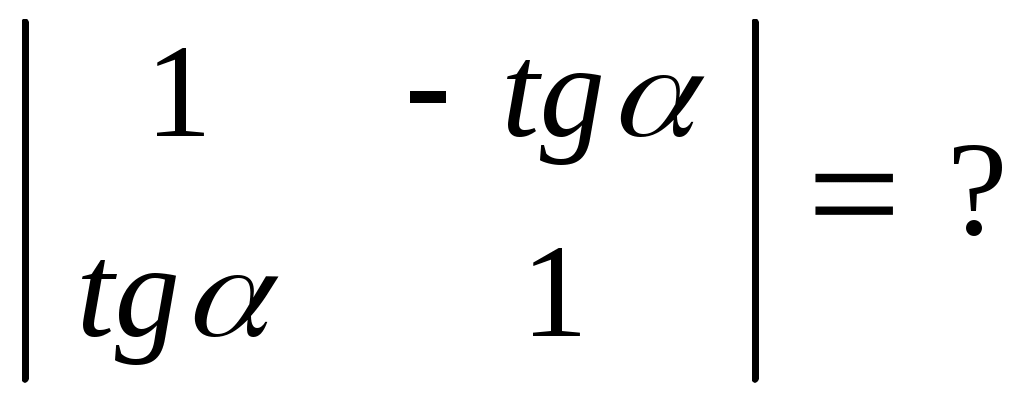
| 1. 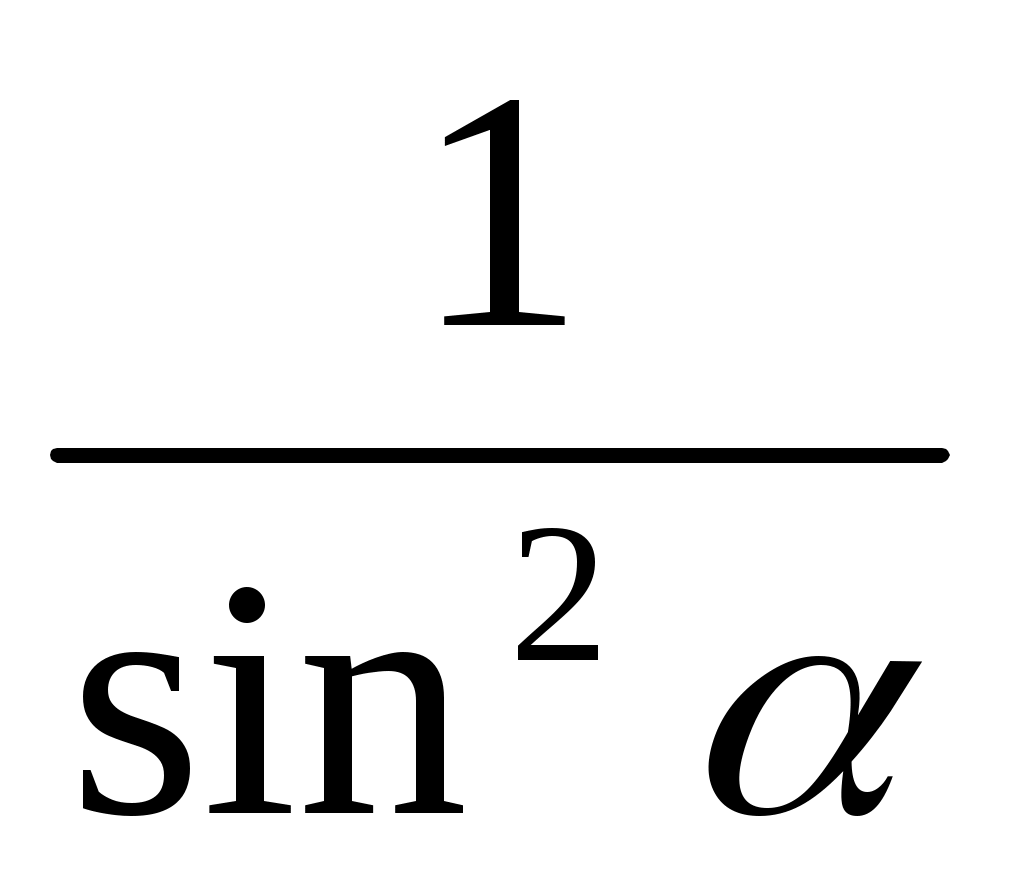 2. 2. 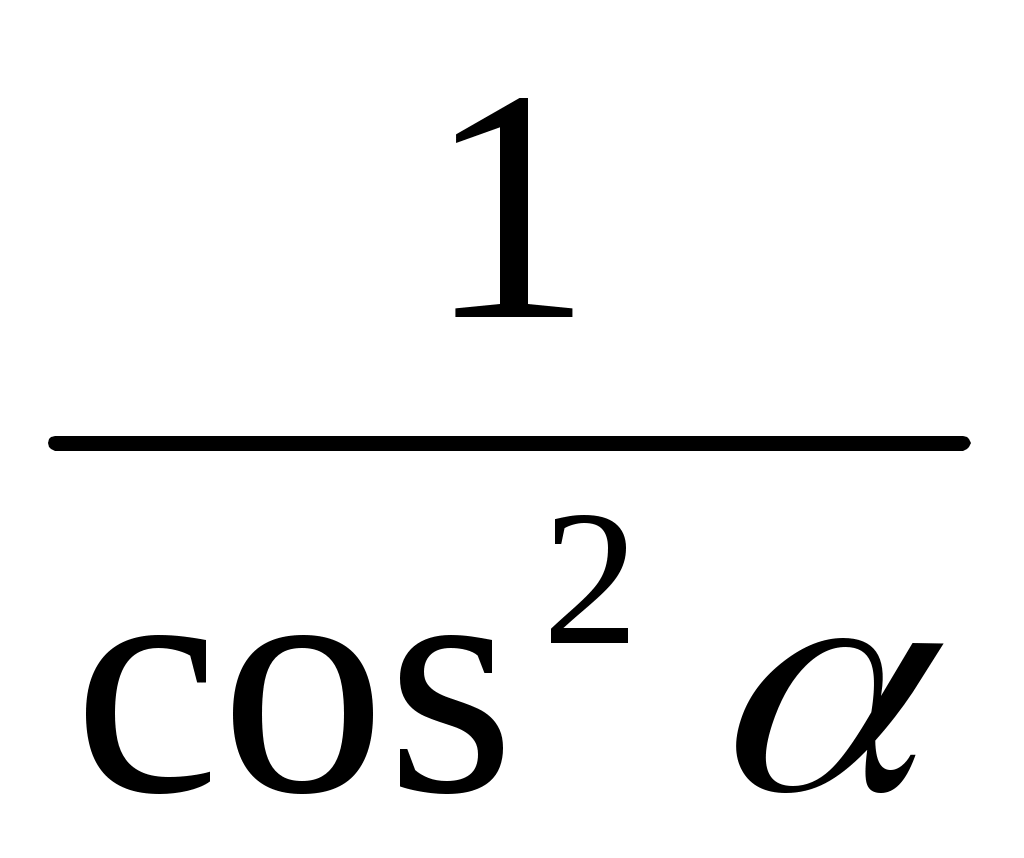 3. 3. 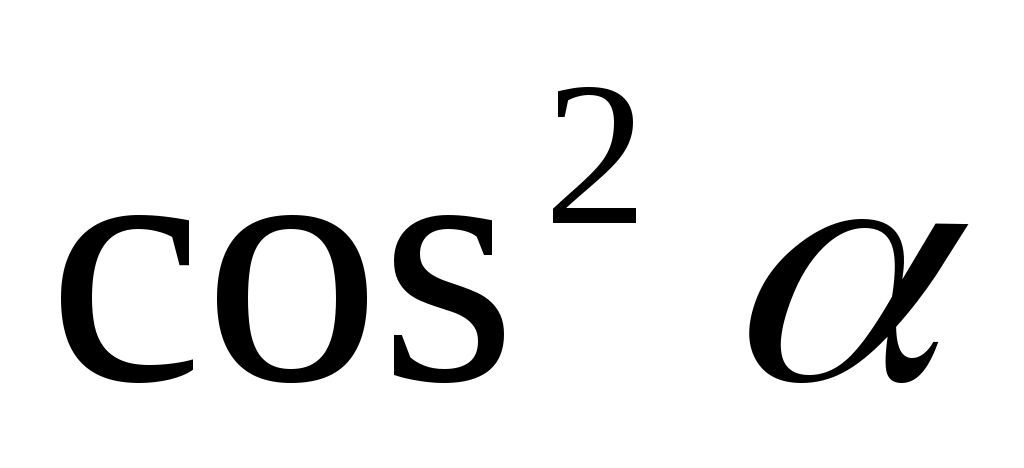  4. 4. 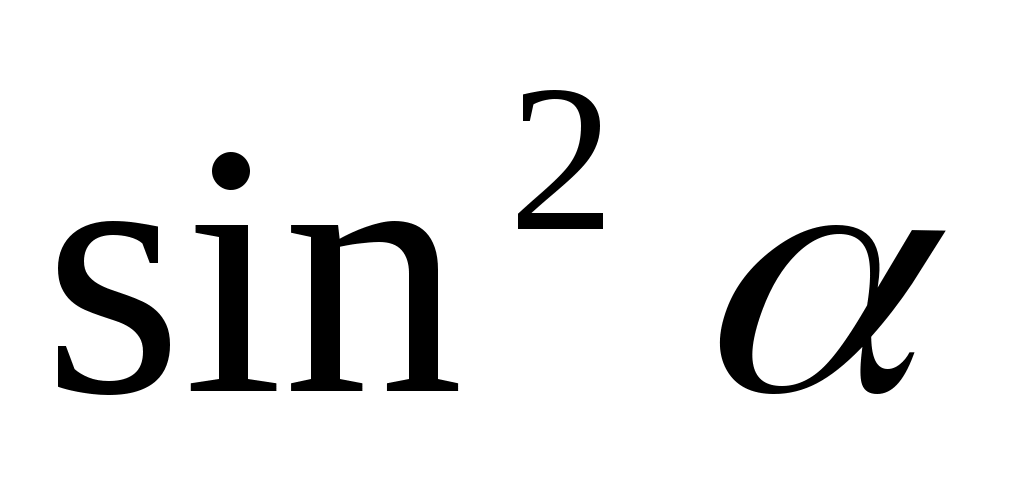 |
100.
|
 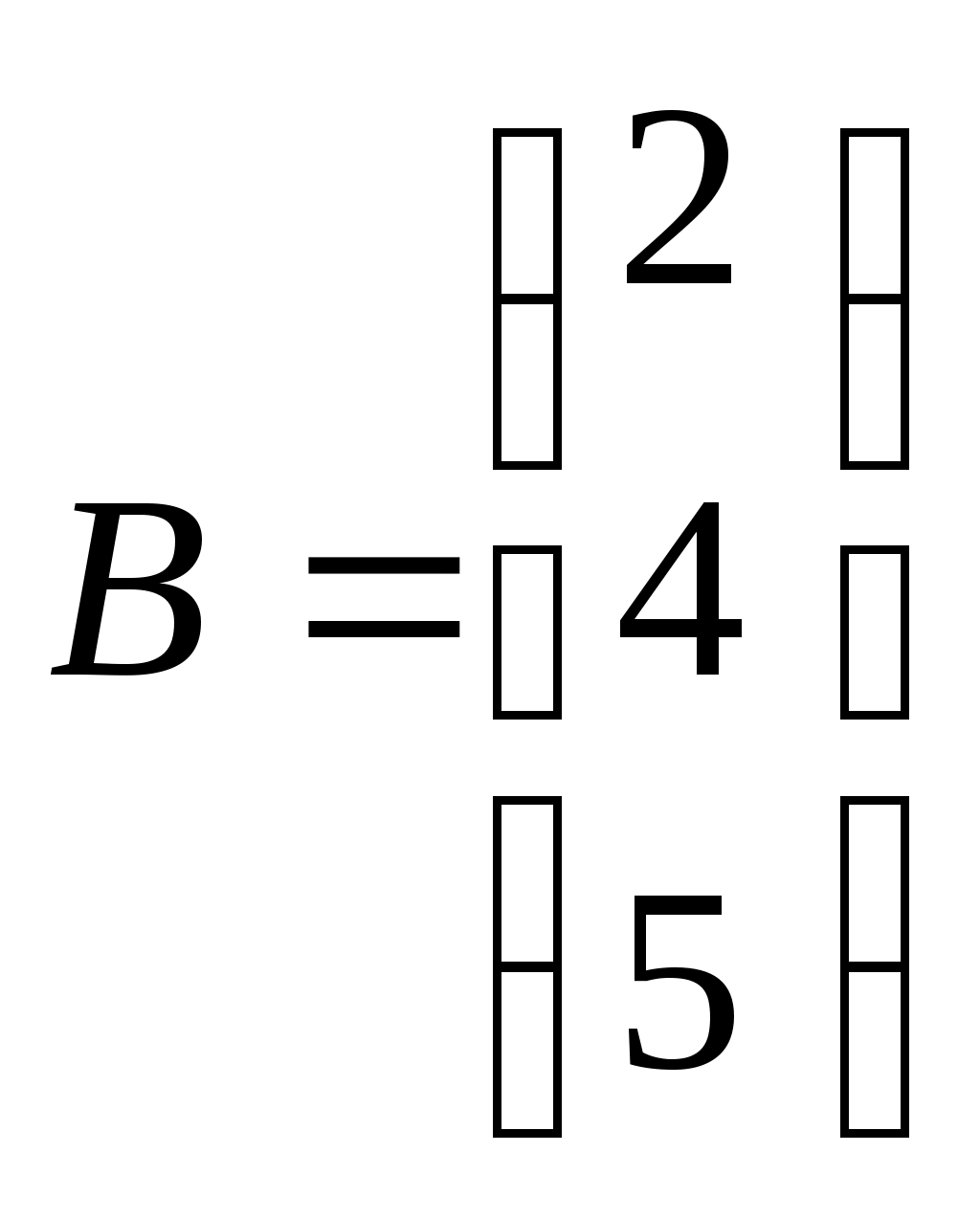 Какая операция невозможна? Какая операция невозможна?
|
1. BA 2. AB 3. 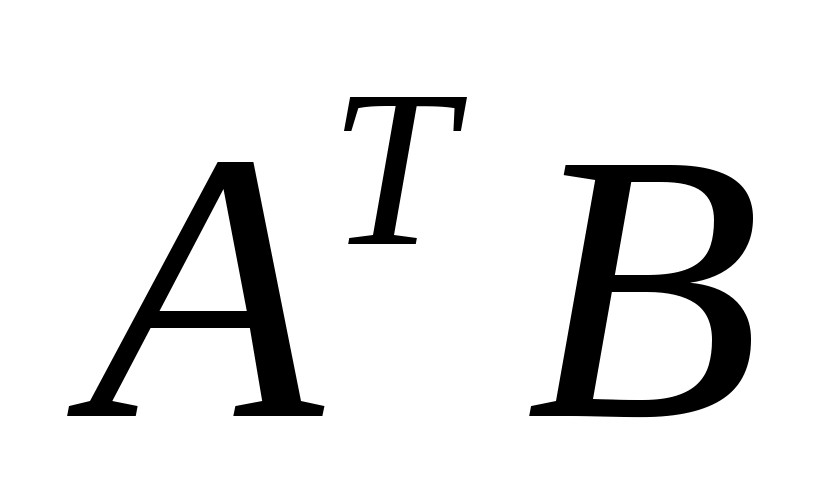 4. 4. 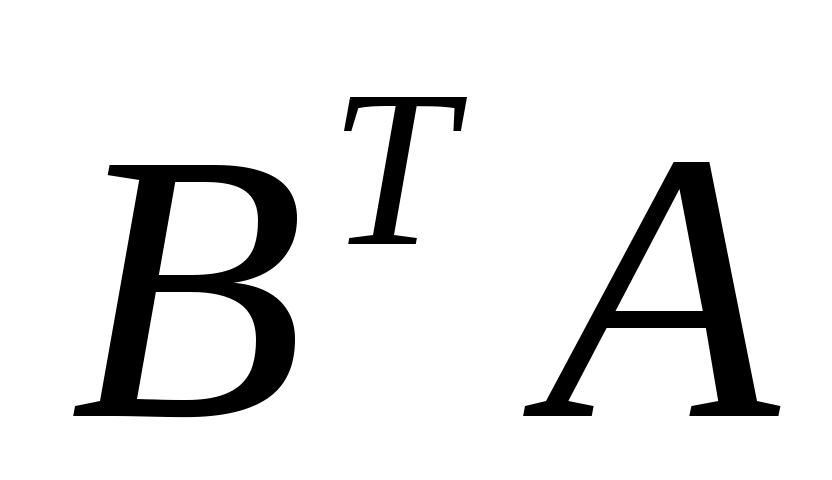
|
 Скачать 0.59 Mb.
Скачать 0.59 Mb.