Линейная алгебра. Тема 1. Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами. Матрица. Основные понятия. Матрицей
 Скачать 431.7 Kb.
|
|
Тема №1. Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами. 1. Матрица. Основные понятия. Матрицей размера называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,…, X, Y, Z, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: , где i – номер строки; j – номер столбца. Например, матрица размеров имеет вид: 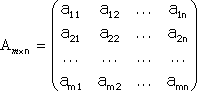 или в сокращенной записи  Например, матрица размеров имеет вид:  . Наряду с круглыми скобками для обозначения матриц используются и другие: Две матрицы А и В одинаковой размерности называются равными, если при всех  Виды матриц Матрица, состоящая из одного столбца, называется матрицей (вектором)-столбцом и обозначается  , а состоящая из одной строки – матрицей (вектором)-строкой, соответственно обозначается  .Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n: 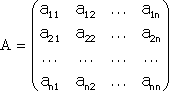 .Элементы  образуют главную диагональ квадратной матрицы порядка n, а элементы – побочную диагональ.Например, – квадратная матрица третьего порядка, элементами главной диагонали являются числа 1, 5, 9, а побочной – 7, 5 ,3. Если все элементы, кроме элементов, образующих главную диагональ квадратной матрицы, равны нулю, то такая матрица называется диагональной. Например 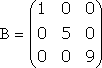 – диагональная матрица третьего порядка.Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка и обозначается буквой Е. Например – единичная матрица третьего порядка. Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О. Нулевая матрица имеет следующий вид: 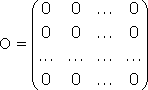 .В линейной алгебре матрицы Е и О играют такую же роль, какую играют числа 1 и 0 в арифметике. Матрица, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается . Пример 1. Так, если  , то  .Транспонированная матрица обладает следующим свойством: . 2. Действия над матрицами 1. Умножение матрицы на число Пусть  – произвольная матрица, – произвольное действительное число.Произведением матрицы А на число называется новая матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число , т.е.  . Например -  Таким образом, можно выделить следующее следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы. 2. Сложение и вычитание матриц. Эта операция определяется только для матриц одинаковой размерности (формата). Суммой двух матриц А и В одинаковой размерности называется новая матрица С того же размера, каждый элемент которой равен сумме соответствующих (стоящих на одинаковых местах) элементов данных матриц. Например, пусть А и В – матрицы размерности . Тогда по определению под суммой понимается 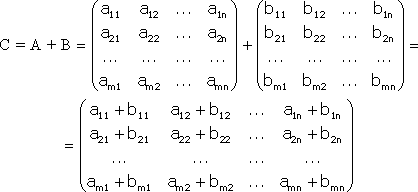 или  .Вышеприведенные действия над матрицами называются линейными. Линейные операции над матрицами обладают следующими свойствами: 1. Переместительность (коммутативность) умножения матрицы на число . 2. Сочетательность (ассоциативность) со скалярным множителем  .3. Переместительность (коммутативность) сложения матриц . 4. Сочетательность (ассоциативность) сложения матриц  .5. Распределительность (дистрибутивность) сложения матриц относительно умножения на число  .6. Распределительность (дистрибутивность) относительно сложения чисел  .Таким образом, линейные операции над матрицами можно выполнять по аналогии с привычными правилами алгебры чисел. Вычитание для матриц (как и для чисел) определяется как действие, обратное сложению. Разностью матриц А и В (А – В) одинаковой размерности называется такая матрица С, что В+С=А. Легко заметить, что матрица С, удовлетворяющая этому условию, всегда существует, и притом только одна. Ее элементы определяются равенствами: . Таким образом, при вычитании матриц вычитаются соответствующие элементы этих матриц. Например,  .Замечание. Знаки сравнения ( ) для матриц любого формата лишены смысла. 3. Умножение матриц. Умножение матрицы А на матрицу В (рассматриваются именно в таком порядке) определено, если число столбцов первой матрицы равно числу строк второй матрицы. В этом случае матрица А называется согласованной с матрицей В. Иначе говоря, если порядок матрицы А равен , то порядок согласованной с ней матрицы В должен быть , где – любые натуральные числа. Произведением матрицы  на матрицу  называется такая матрица  , что , где Таким образом, для вычисления элемента , стоящего в строке и в столбце матрицы С, следует каждый элемент строки матрицы А умножить на соответственный элемент столбца матрицы В и результат сложить. Примеры: 1)  .2) 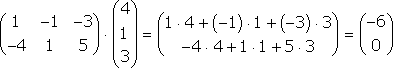 .Умножение матриц обладает следующими свойствами: 1)  ;2)  ;3)  ;4)  .Заметим, что умножение матриц некоммутативно: . Выше было определено, что операция умножения имеет место только для согласованных матриц А и В, при этом матрицы, взятые в ином порядке (В и А), могут оказаться несогласованными, тогда их произведение не определено. Но даже в том случае, когда согласованность матриц не нарушается, произведения АВ и ВА могут оказаться разными. Например, для матриц и  имеем: , но .Если АВ=ВА, то матрицы А и В называются перестановочными (коммутирующими). Очевидно, это может иметь место только в том случае, когда А и В – квадратные матрицы одного и того же порядка. Например, коммутирующими являются матрицы:  и  .Действительно,   ,то есть для данных матриц АВ=ВА. Еще одно замечание: произведение двух матриц может быть нуль-матрицей, даже если ни один из сомножителей не является нуль-матрицей. Например, пусть даны матрицы  и  . Найдем произведение АВ и ВА: ;  . Отсюда следует, что умножение матриц обладает рядом свойств, не характерных для умножения действительных чисел, поэтому при действиях с матрицами необходимо проявлять осмотрительность и аккуратность. В заключение, отметим свойства, присущие операции транспонирования: 1)  ;2)  ;3)  .4. Возведение в степень. На основе определения произведения матриц умножать матрицу А на себя можно только в том случае, если это квадратная матрица. Пусть k – целое неотрицательное число, тогда k – й степенью квадратной матрицы А называется матрица, которая вычисляется следующим образом: 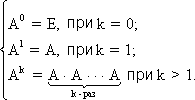 Пример. Найти куб матрицы  . ; .Тема №2. Теория определителей. Основные свойства определителей. Вычисление определителей произвольного порядка n. Формулы разложения. 1. Определители Понятие определителя вводится лишь для квадратных матриц. Любой квадратной матрице А порядка n ставится в соответствие по определенному закону некоторое число, называемое определителем или детерминантом n–го порядка этой матрицы. Для записи определителя матрицы А используются следующие обозначения: , , , или развернутое, учитывающее связь с элементами заданной матрицы 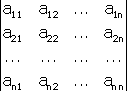 , где вертикальные линии вместо круглых (матричных) скобок указывают на то, что здесь речь идет об определителе матрицы А (о единственном числе), а не о таблице чисел.Числа  в этом случае называются элементами определителя. При этом, как и в матрице А, элементы образуют главную диагональ определителя, а элементы – побочную.Введем понятие определителя сначала для квадратных матриц первого, второго и третьего порядка, а затем распространим на квадратные матрицы любого порядка. Определителем матрицы , то есть матрицы, состоящей из одного элемента (определителем первого порядка), называется само число . Пусть дана квадратная матрица второго порядка  , тогда ее определителем (определителем второго порядка) называется число  .Пример 1. Найти определитель матрицы  .Решение:  Пусть дана квадратная матрица третьего порядка 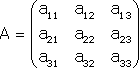 , тогда определителем третьего порядка данной матрицы называется число, которое вычисляется следующим образом: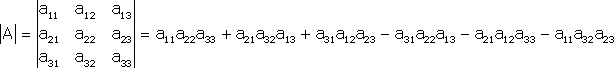 Замечание. При вычислении определителя третьего порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать следующим образом:  Пример. Вычислить определитель матрицы 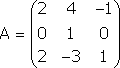  .2. Свойства определителей Рассмотрим свойства определителей второго и третьего порядков. Свойство 1. Определитель квадратной матрицы равен определителю ее транспонированной матрицы: . Докажем это свойство для определителя второго порядка. Действительно,  ,  , то есть .Свойство 2. При перестановке столбцов (строк) определитель меняет только знак. Действительно, если , то Замечание. В дальнейшем для упрощения формулировок свойств определителей строки и столбцы матрицы будем называть рядами. Свойство 3. Если какой-нибудь ряд матрицы является линейной комбинацией некоторых параллельных ему рядов, то определитель этой матрицы равен нулю. Действительно, пусть имеется следующая квадратная матрица третьего порядк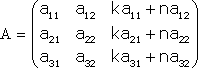а:  , тогда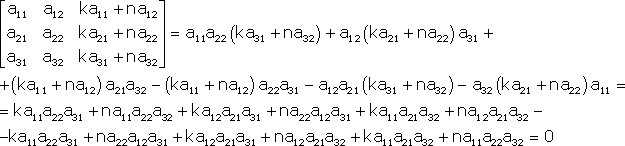 Следствие 1. Определитель, имеющий одинаковые параллельные ряды, равен нулю. Следствие 2. Определитель, содержащий ряд из одних нулей, равен нулю. Свойство 4. Если каждый элемент какого-либо ряда определителя есть сумма двух слагаемых, то определитель равен сумме двух определителей, у одного из которых элементами соответствующего ряда являются первые слагаемые, у другого – вторые, а остальные элементы этих двух определителей те же, что у данного:  . Действительно, 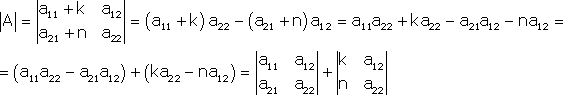 Свойство 5. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. Действительно,  Свойство 6. Определитель не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число. Действительно, на основании свойств 4 и 5  и, согласно следствию 1, второй определитель равен нулю, следовательно .Для формулировки следующих свойств определителей возникает необходимость введения понятий минора и алгебраического дополнения. Введем понятие минора для элементов определителя третьего порядка. Пусть имеется определитель третьего порядка  .Возьмем элемент  .Вычеркнем в ней -ю строку и -ый столбец и сдвинем, не нарушая порядка, оставшиеся элементы. Определитель полученной матрицы 2-го порядка называется минором элемента -ой строчки и -го столбца матрицы А и обозначается . Например, минор элемента обозначают . Таким образом, по определению для определителя  ,  ,  ,  и т.д.Введем понятие минора для определителя n-го порядка 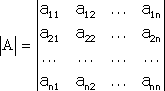 . Выделим в нем какой-либо элемент и вычеркнем строку и столбец, на пересечении которых расположен этот элемент. Полученный определитель (n-1)-го порядка называется минором элемента определителя . Алгебраическим дополнением элемента квадратной матрицы порядка n называется число, рассчитанное по формуле  .Согласно этой формуле, алгебраическое дополнение совпадает с минором , если сумма индексов является четным числом и имеет знак, противоположный знаку минора , если сумма индексов – нечетное число. 3. Вычисление определителей произвольного порядка n. Формулы разложения Теорема. Определитель третьего порядка равен сумме произведений элементов любого его ряда на соответствующие им алгебраические дополнения, то есть:  ;  ;  ;  ; ;  . Пример. Найти определитель 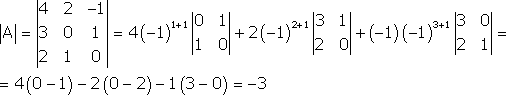 Данная теорема справедлива и для определителя n-го порядка. Определитель n-го порядка равен сумме произведений любого его ряда на соответствующие им алгебраические дополнения, то есть  ; Данные равенства называют разложениями определителя (формулами разложения) по строке или по столбцу соответственно. Все свойства, доказанные выше для определителей второго и третьего порядков, справедливы и для определителя n-го порядка. В завершении приведем еще два важных свойства определителей. Свойство 7. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Докажем данное свойство для определителя третьего порядка. С этой целью вычислим сумму произведений элементов первой строки матрицы на алгебраические дополнения соответствующих элементов третьей строки: 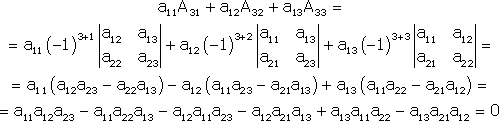 Свойство 8. Определитель произведения двух квадратных матриц равен произведению определителей этих матриц. Докажем это свойство для квадратных матриц второго порядка. Пусть 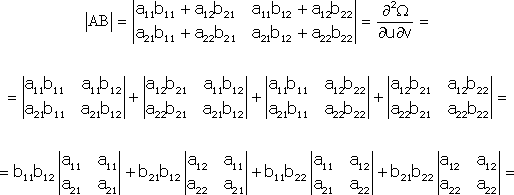 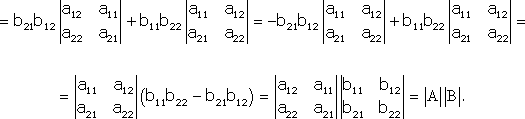тогда с учетом свойств определителей  |