Линейная алгебра. Тема 1. Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами. Матрица. Основные понятия. Матрицей
 Скачать 431.7 Kb. Скачать 431.7 Kb.
|
Тема №3. Обратная матрица. Ранг матрицы. Понятие обратной матрицы
Примечание. Матрица, полученная из данной с помощью элементарных преобразований, называется эквивалентной этой матрице. Эквивалентность матриц обозначается знаком . С помощью элементарных преобразований матрицу можно привести к ступенчатому виду: 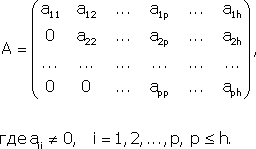 Ранг полученной ступенчатой матрицы равен p. Пример. Найти ранг матрицы 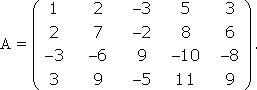 Решение. Приведем матрицу А к ступенчатому виду с помощью элементарных преобразований: 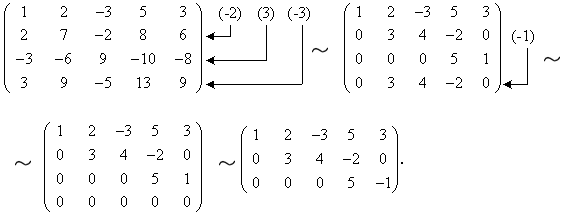 Полученная ступенчатая матрица содержит три ненулевых строки, а это означает, что ее ранг равен 3. Следовательно, ранг исходной матрицы также равен 3. Тема №4. Системы линейных алгебраических уравнений 1. Системы линейных алгебраических уравнений Системой линейных алгебраических уравнений (СЛАУ) называется система вида 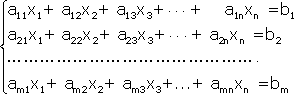 (4.1) (4.1) Решением системы (4.1) называется такая совокупность n чисел Решить систему означает найти все ее решения или доказать, что ни одного решения нет. СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет. Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение. Например, система уравнений несовместная, а система Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными. Основной матрицей СЛАУ (4.1) называется матрица А размера , элементами которой являются коэффициенты при неизвестных данной системы, то есть 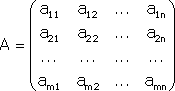 . .Матрицей неизвестных СЛАУ (4.1) называется матрица-столбец Х, элементами которой являются неизвестные системы (4.1): 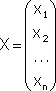 . . Матрицей свободных членов СЛАУ (4.1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ: 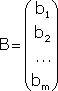 . . С учетом введенных понятий СЛАУ (4.1) можно записать в матричном виде или 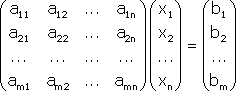 . (4.2) . (4.2) 2. Решение систем линейных уравнений. Метод обратной матрицы Перейдем к изучению СЛАУ (4.1), которой соответствует матричное уравнение (4.2). Сначала рассмотрим частный случай, когда число неизвестных равно числу уравнений данной системы ( ) и , то есть основная матрица системы невырождена. В этом случае, согласно предыдущему пункту, для матрицы существует единственная обратная матрица . Ясно, что она согласована с матрицами и . Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу : Следовательно, с учетом свойств умножения матриц получаем Так как , а , тогда . (4.3) Убедимся, что найденное значение является решением исходной системы. Подставив (4.3) в уравнение (4.2), получим Покажем, что это решение единственное. Пусть матричное уравнение (4.2) имеет другое решение , которое удовлетворяет равенству . Покажем, что матрица равна матрице С этой целью умножим предыдущее равенство слева на матрицу. В результате получим 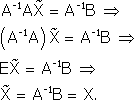 Такое решение системы уравнений с неизвестными называется решением системы (4.1) методом обратной матрицы. Пример. Найти решение системы 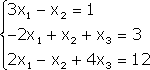 Выпишем матрицу системы: 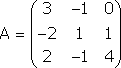 , , Для этой матрицы ранее (занятие 1) мы уже нашли обратную: 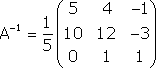 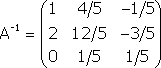 или или Здесь мы вынесли общий множитель , так как нам в дальнейшем нужно будет произведение . Ищем решение по формуле: . 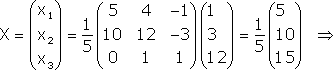 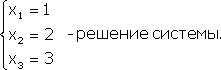 Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением. Упражнение. Проверку этого факта сделайте самостоятельно. 3. Правило и формулы Крамера Рассмотрим систему линейных уравнений с неизвестными 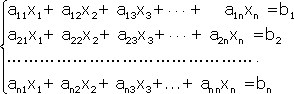 От матричной формы (4.3) перейдем к более удобным и в ряде случаев более простым при решении прикладных задач формулам для нахождения решений системы линейных алгебраических уравнений. Учитывая равенство , или в развернутом виде 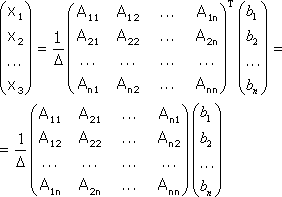 . . Таким образом, после перемножения матриц получаем: 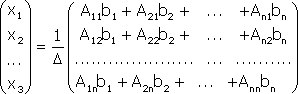 или или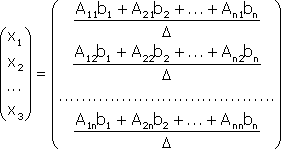 . .Заметим, что сумма 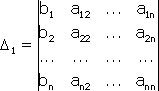 по элементам первого столбца, который получается из определителя путем замены первого столбца коэффициентов столбцом из свободных членов. Таким образом, можно сделать вывод, что Аналогично: , где получен из путем замены второго столбца коэффициентов столбцом из свободных членов, Следовательно, нами найдено решение заданной системы по равенствам , , известным и как формулы Крамера. Для нахождения решения СЛАУ, последние равенства можно записать в общем виде следующим образом: Согласно этим формулам, имеем правило Крамера для решения СЛАУ: - по матрице системы вычисляется определитель системы ; - если , то в матрице системы каждый столбец последовательно заменяется столбцом свободных членов и вычисляются определители - решение системы находится по формулам Крамера (4.4). Пример. С помощью формул Крамера решить систему уравнений 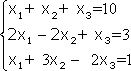 |

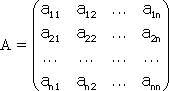
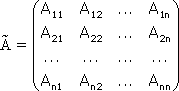
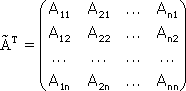 .
. 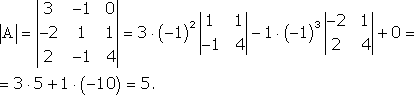
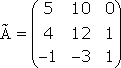
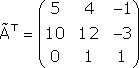
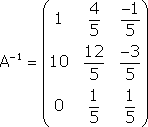
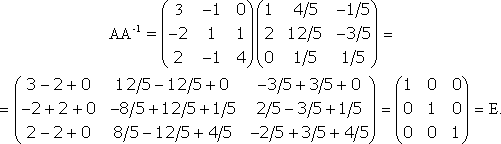
 .
.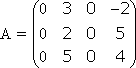 .
.