Ргр по сгм. Раздел
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
ОГЛАВЛЕНИЕ ВВЕДЕНИЕ………...……………………………………………………………..3 Раздел 1. СИСТЕМА Mathcad……….………………………………………....4 1.1 Возможности "Mathcad" ……………………………………………….…..…5 1.2 Основы языка……………………..………..………………………………….6 1.3 Шесть правил вычислений в среде «Mathcad»……………...………………9 Раздел 2. ОБРАТНАЯ МАТРИЦА И ЕЕ ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ….......................13 2.1 Основное определение………………………………………………………13 2.2 Основные свойства обратной матрицы …………………………..………..13 2.3 Обратная матрица на нескольких примерах………………………...……14 2.4 Теорема и доказательство невырожденной матрицы……………………..15 2.5 Метод элементарных преобразований……………………………………..17 Раздел 4. ОТЧЕТЫ ПО ЛАБОРАТОРНЫМ РАБОТАМ………….……...19 ЗАКЛЮЧЕНИЕ…………………………………………..…………………….20 СПИСОК ЛИТЕРАТУРЫ…………………………………………………….21 ВВЕДЕНИЕ Компания MathSoft ведущий производитель математического, научного и инженерного программного обеспечения. В России чрезвычайной популярностью пользуется пакет Mathcad, с помощью которого решают свои задачи ученые и инженеры, студенты и школьники. Mathcad позволяет, используя удобный графический интерфейс и приближенный к естественному математическому язык описания задач, автоматизировать численные расчеты и аналитические преобразования и наглядно представить результаты. Mathcad - программное средство, среда для выполнения на компьютере разнообразных математических и технических расчетов, снабженная простым в освоении и в работе графическим интерфейсом, которая предоставляет пользователю инструменты для работы с формулами, числами, графиками и текстами. В среде Mathcad доступны более сотни операторов и логических функций, предназначенных для численного и символьного решения математических задач различной сложности. MathCAD - это мощная и в то же время простая универсальная среда для решения задач в различных отраслях науки и техники, финансов и экономики, физики и астрономии, математики и статистики… MathCAD остается единственной системой, в которой описание решения математических задач задается с помощью привычных математических формул и знаков. MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математикоориентированный интерфейс и прекрасные средства научной графики. Система MathCAD существует в нескольких основных вариантах: • MathCAD Standard - идеальная система для повседневных технических вычислений. Предназначена для массовой аудитории и широкого использования в учебном процессе; • MathCAD Professional - промышленный стандарт прикладного использования математики в технических приложениях. Ориентирована на математиков и научных работников, проводящих сложные и трудоемкие расчеты. • MathCAD Professional Academic - пакет программ для профессионального использования математического аппарата с электронными учебниками и ресурсами. СИСТЕМА Mathcad Mathcad является уникальной системой для научных и инженерных расчетов и позволяет работать с формулами, числами, текстом и графиками. С помощью системы Mathcad можно решить почти любую математическую задачу символьно либо численно. Mathcad позволяет записывать на экране компьютера формулы в их привычном виде. Mathcad имеет свою собственную справочную систему. Электронные Книги делают доступными для использования в рабочем документе множество полезных формул, справочных данных и диаграмм простым нажатием кнопки. Объединяя в одном рабочем листе текст, графику, и математические выкладки, Mathcad облегчает понимание самых сложных вычислений. Особенности Mathcad: Полная совместимость с Windows: изменение размеров окон и их перемещение, открытие нескольких окон, поддержка мыши. Возможность комбинирования текста, математических выкладок и графики в любом месте экрана. Встроенный алгоритм решения систем уравнений и неравенств. Действия с производными и интегралами. Вычисление сумм рядов, произведений и итерации. Тригометрические, гиперболические, экспоненциальные и Бесселевы функции. Статистические функции, включая линейную регрессию, гамма- функцию Эйлера, интеграл ошибок, функции вероятностных распределений. 1.1 Возможности "Mathcad" Пакет программ "Mathcad" позволяет выполнять математические расчёты с помощью компьютера в среде операционной системы "Windows". "Mathcad" включает в свой состав три редактора - формульный, текстовый и графический. Благодаря им обеспечивается принятый в математике способ записи функций и выражений и получение результатов вычислений, произведенных компьютером, в виде таблиц и графиков. Взаимодействие пользователя с компьютером осуществляется с помощью удобного графического интерфейса, включающего пиктограммы, диалоговые окна, меню опции и другие "инструменты", располагаемые на экране дисплея. "Mathcad" включает множество операторов, встроенных функций и алгоритмов решения разнообразных математических задач, которые прямо приложимы ко всему комплексу вопросов, рассматриваемых в рамках самых разнообразных научно-технических дисциплин. "Mathcad" обладает повышенной точностью и быстродействием вычислений повышенной степени сложности, используя 32-разрядную память. С помощью «Mathcad» можно решать следующие математические задачи   1.2 Основы языка Язык, на котором изъясняются в среде «Mathcad» для изображения констант, переменных величин, операторов, функций, уравнений и иных математических записей, практически полностью совпадает с общепринятым в математике. Громадный набор стандартных функций: тригонометрических и обратных им, гиперболических и обратных им, показательных и логарифмических, функций комплексного аргумента, специальных (Беcселя, Чебышева, Лагера, Лэжандра, Эрмита, гамма и других), статистических, финансовых, связанных с разнообразными преобразованиями и поиском оптимальных решений и т. д., представлены подменю "Встроенные функции" и на математических инструментальных панелях. Путем обращения к этим встроенным в пакет «Mathcad» функциям можно выполнять самые разнообразные компьютерные вычисления. Знаки всех математических операций, как арифметических (сложение, вычитание, деление, возведение в степень, извлечение корня и т. д.), так и относящихся к высшей математике (интегрирование, дифференцирование, связанных с матричным и векторным исчислением и т. д.) в пакете «Mathcad» совладают с общепринятыми в математике.    Весьма важным здесь является подменю "Функции f(x)", вынесенное также на стандартную линейку. Меню «Формат». Здесь расположены команды, позволяющие придать определенную форму создаваемому документу: разделить его на области, выбрать цвет, тип и размер шрифта надписей, придать определенный вид исходным данным, уравнениям и результатам вычислений. Весьма важной для вычислений здесь является опция "Результат", после исполнения которой появляется окно, позволяющее установить форму результата и его точность (до 15-го знака после запятой). Меню "Математика". Здесь сосредоточены опции, относящиеся к процессу вычисления, в том числе к его автоматизации. Меню "Символы". Данное меню включает операции символьной математики: преобразование выражений, разложение многочлена на множители, определение коэффициентов полинома и его корней, интегрирование и дифференцирование функций. Меню "Окно". С помощью команд этого меню можно придать определенный вид расположению окон, например, по вертикали, горизонтали или каскадом, содержащие определенные рабочие документы «Mathcad». Меню "?" (справка) предоставляет возможность получить разнообразную информацию справочного характера по работе в среде «Mathcad». Ниже с помощью примеров будет раскрыто содержание и процедура пользования различными подменю, командами и опциями из перечисленных меню. Вторая строка текстового окна, называемая стандартной линейкой, включает наиболее часто используемые операции, каждой из которых соответствует определенная пиктограмма, смысл которой раскрывается ее изображением. При установке курсора на пиктограмме под ней появляется надпись, поясняющая ее назначение, а при одном щелчке левой клавишей "мыши" осуществляется выполнение соответствующей команды. Все пиктограммы дублируют наиболее часто используемые команды, содержащиеся в меню. Такое дублирование ускоряет работу с программой, позволяя ту или иную команду выполнить в один, а не в два приема. Третья строка текстового окна называется линейкой форматирования. В ней представлены наиболее важные команды только из одного меню - форматирования, определяющего внешнюю форму напечатанного документа. При помощи линейки форматирования можно выбрать требуемый вид, размер и толщину шрифта, выровнять текст, дать нумерацию абзацам и выполнить другие команды. При установке курсора на значке под ним появляется надпись, раскрывающая его назначение, а при одном щелчке осуществляется выполнение соответствующей команды. Панель "Математика" из меню "Вид", можно постоянно расположить в текстовом окне в качестве 4-й строки. 1.3 Шесть правил вычислений в среде «Mathcad» Возможны два типа вычислений в среде «Mathcad», осуществляемые с помощью формульного редактора: численный и символьный. При первом типе результат получается в виде числа, при втором - в форме математического выражения. Реализация численного способа осуществляется: - путем обращения к панелям математических инструментов из меню "Вид";  Реализация символьного способа, при котором происходит преобразование одного математического выражения в другое, осуществляется:  Запись математических выражений в составляемую программу осуществляется с помощью математических инструментальных панелей, путем обращения к встроенным функциям f(x) и с помощью клавиатуры. В том месте рабочей области текстового окна, где установлен курсор-стрелка, после щелчка левой клавиши "мыши" возникает визир в форме значка + красного цвета. На месте установки визира отражается результат той или иной команды или операции и происходит ввод в программу требуемого математического выражения. После ввода первого символа визир преобразуется в две линии - горизонтальную и вертикальную - синего цвета. Перемещение визира осуществляется с помощью "мыши" при нажатой левой клавиши или клавиш клавиатуры, ответственных за перемещение курсора. Сформулируем шесть правил, которыми следует пользоваться при реализации численного и символьного методов решения разнообразных математических задач в среде «Mathcad». Данные правила, позволяющие одну и ту же задачу решать разными способами, 1-е правило, связанное с обращением к панелям математических инструментов из меню "Вид": "Арифметика", "Матрицы" и "Математический анализ" (Исчисления"), позволяет получить результат в виде числа. Сначала щелчком вызывается соответствующую панель инструментов, а затем производится щелчок по требуемой пиктограмме (кнопке), после чего в рабочей области текстового окна в месте установки красного визира появляется определенное выражение. Вписывание в него исходных данных и ввод знака равенства дает числовой результат. 2-е правило, связанное с обращением к встроенным функциям f(x) из меню "Вставка", позволяет получить результат в виде числа. Производится обращение к пиктограмме "Встроенная функция f(x)" на 2-й строке текстового окна - стандартной линейке. На появившемся после щелчка диалоговом окне в разделе "Категория функций" выбирается определенное имя, а в разделе "Название функции" - требуемая функция. После нажатия на кнопку "ОК" или "Вставить" в рабочей области тестового окна появляется выбранная функция, в которую вписываются заданные числа и вводится знак =, после чего автоматически получается результат. 3-е правило, связанное с вводом необходимых знаков с помощью клавиатуры, позволяет получить результат, как в численном, так и символьном виде. Данное правило, по существу, аналогично двум предыдущим. Только здесь все знаки - числа, арифметические действия и латинские обозначения - вводятся в текст составляемой программы с помощью клавиатуры. Возможен ввод и специальных операторов при символьных вычислениях путем одновременного нажатия двух или трех клавиш. 4-е правило, связанное с обращением к математической панели инструментов "Символы", позволяет получить результат как в сим¬вольном, так и численном виде. Математическое выражение, подлежащее преобразованию, запи-сывается в рабочей области текстового окна и с помощью курсора обрамляется рамкой. Далее в зависимости от вида преобразования . выбирается соответствующее ключевое слово: Series - при разложении функции в степенной ряд Маклорена по выбранной переменной; Expland- при разложении в степенной ряд выражений типа бинома Ньютона; Complex - при преобразовании комплексных чисел; Символьный знак равенства → при дифференцировании, и т.д. После щелчка по выбранному ключевому слову к записи автоматически добавляется это слово и символический знак равенства →, После второго щелчка вне рамки записи автоматически появляется результат в виде нового символьного выражения, полученного из исходного в результате преобразования. 5-е правило, связанное с обращением к меню "Символы", подменю "Расчеты", позволяет произвести символьные вычисления, в том числе и в комплексной области. Математические выражения, связанные между собой определенными операциями, записываются в рабочей области текстового окна, и с помощью курсора обрамляется рамкой. Далее щелчком производится обращение к строке "символические" при дифференцировании и интегрировании функций и других операциях, а при работе с комплексными числами - к строке "комплексные". После щечка на рабочем листе появляется результат в виде нового выражения, располагаемого под исходной записью. 6-е правило, также связанное с обращением к меню "Символы", позволяет произвести разнообразные символьные преобразования, записав в рабочей области текстового окна подлежащее преобразованию выражение. При обращении к подменю "Переменные" в этом выражении необходимо выделить (затемнить) один символ - переменную - путем протаскивания курсора. Далее с помощью подменю "Переменные" можно выполнить следующие операции: -найти корни алгебраического и трансцендентного уравнений (опция "Вычислить"); -произвести дифференцирование функции (строка "Дифференциалы"); -произвести интегрирование функции (строка "Интеграция"); -разложить функцию в степенной ряд Маклорена (строка "Разложить на составляющие"); -разложить функцию на элементарные дроби (строка "Преобразовать в частичные доли"). При обращении к подменю "Матрица" следует обрамить рамкой все выражение. Это подменю позволяет осуществить транспонирование и обращение (инвертирование) матрицы и найти ее определитель. При обращении к подменю "Преобразования" можно произвести прямое и обратное преобразования: Фурье, Лапласа и типа Z. ОБРАТНАЯ МАТРИЦА И ЕЕ ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ 2.1 Основное определение Обратной матрицей к матрице A называется такая матрица B, что AB = BA = E. Обозначается обратная матрица Обратная матрица единственна! 2.2 Основные свойства обратной матрицы  Для матрицы 2х2 легко можно найти обратную матрицу по определению. 2.3 Обратная матрица на нескольких примерах  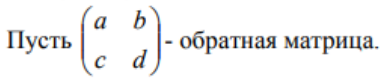 Тогда 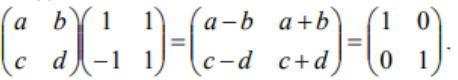  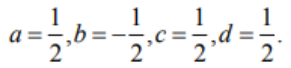 Следовательно 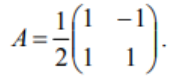 В случае матрицы 3-го порядка уже понадобилось бы решать систему из 9 уравнений, что уже вызывает большие трудности Еще один пример: 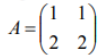 Значит 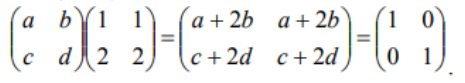 Получим систему  Значит, как мы убедились, обратная матрица существует не для любой матрицы. Квадратная матрица, определитель которой равен нулю, называется вырожденной. Соответственно, невырожденной называется квадратная матрица, определитель которой не равен нулю. 2.4 Теорема и доказательство невырожденной матрицы Теорема: Для того чтобы матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной. Доказательство теоремы для того, чтобы понять, как вычислять обратную матрицу:   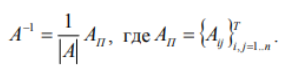 Для матрицы 2-го порядка метод присоединенной матрицы является очень эффективным, так как не надо вычислять определители, а алгебраические дополнения – это всего лишь элементы матрицы. С другими матрицами большого порядка это сделать не получится, будет сложно, поэтому мы используем метод элементарных преобразований. 2.5 Метод элементарных преобразований Элементарными преобразованиями строк матрицы называются: 1. Перестановка местами любых двух строк матрицы; 2. Умножение одной строки матрицы на ненулевую константу; 3. Прибавление к любой строке матрицы другой строки, умноженной на некоторую константу. Пример: 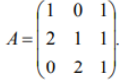 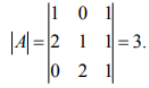 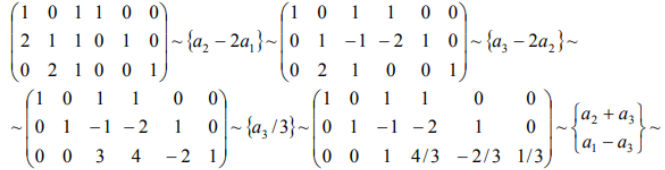 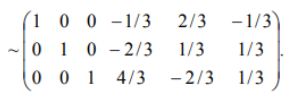 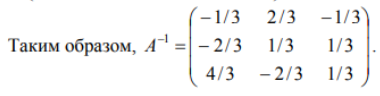 Раздел 4. ОТЧЕТЫ ПО ЛАБОРАТОРНЫМ РАБОТАМ • Отчет по лабораторной работе №1 “АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ” • Отчет по лабораторной работе №2 “ФУНКЦИИ” • Отчет по лабораторной работе №3 “ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ” • Отчет по лабораторной работе №4 “МАТРИЦЫ” • Отчет по лабораторной работе №5 “РЕШЕНИЕ УРАВНЕНИЙ” • Отчет по лабораторной работе №6 “ПОСТРОЕНИЕ ГРАФИКОВ” • Отчет по лабораторной работе №7 “РЯДЫ ФУРЬЕ” ЗАКЛЮЧЕНИЕ В ходе курса я научился с помощью системы «MathCAD» проводить статистические вычисления и анализ, решать систему дифференциальных уравнений, производить дифференцирование и интегрирование функций, осуществлять различные логические операции. Так же для выполнения этих и других функций системы «MathCAD», освоил её язык (символы, знаки) и шесть правил вычислений в её среде. Подробно разобрал доказательство к теореме невырожденной матрицы. Для умножения одной строки матрицы на ненулевую константу, прибавления и перестановки мест строк матрицы воспользовался методом элементарных преобразований строк матрицы. СПИСОК ЛИТЕРАТУРЫ 1. Mathcad 12: Е. Р. Алексеев, О. В. Чеснокова – Санкт–Петербург, НТ Пресс, 2005 г.– 352 с. 2. Mathcad 11/12/13 в математике. Справочник (+ CD–ROM): В. П. Дьяконов – Москва, Горячая Линия – Телеком, 2007 г.– 960 с. 3. Mathcad 12. Для студентов и инженеров: Валерий Очков – Москва, БХВ–Петербург, 2005 г. – 464 с. 4. Mathcad 12. Наиболее полное руководство (+ CD–ROM): Дмитрий Кирьянов – Москва, БХВ–Петербург, 2005 г.– 566 с. 5. Mathcad (+ CD–ROM): Евгений Макаров – Санкт–Петербург, Питер, 2009 г.– 384 с. 6. https://portal.tpu.ru/SHARED/s/STO/Method/Tab4/Новиковский %20Е.А.%20-%20Работа%20в%20MathCAD.pdf 7. http://www.math.mrsu.ru/text/courses/mcad/vvedenie.htm |
