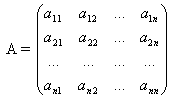Ответ Оп Матрицей a размерности Sxn называется прямоугольная таблица из чисел, состоящая из s строк и n столбцов
 Скачать 7.71 Mb. Скачать 7.71 Mb.
|
Ответ: Опр1. Матрицей A размерности Sxn называется прямоугольная таблица из чисел, состоящая из S строк и n столбцов.  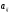 - элемент матрицы, - элемент матрицы,i – номер строки, j – номер столбца. 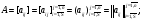 Типы матриц: 1.  квадратная матрица; квадратная матрица;2. 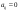 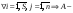 нульматрица; нульматрица;3. 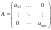 ; A – диагональная матрица ; A – диагональная матрица  элементы главной диагонали. элементы главной диагонали.4.  единичная матрица. единичная матрица.5. 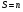 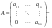 верхняя треугольная матрица. верхняя треугольная матрица.6. 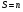 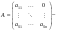 нижняя треугольная матрица нижняя треугольная матрицаОпределение2 Пусть матрицы А и В имеют одинаковую размерность, тогда 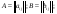 Пусть 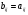 для для  , тогда говорят, что матрицы А и В равны: А=В. , тогда говорят, что матрицы А и В равны: А=В.Определение3 Пусть матрицы А и В имеют одинаковую размерность,  тогда суммой матриц А и В называется матрица тогда суммой матриц А и В называется матрица 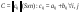 С=А+В; Определение4 Пусть 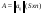 , а , а  вещественное число, тогда произведением матрицы А на число вещественное число, тогда произведением матрицы А на число  называется матрица называется матрица    Свойства линейных операций над матрицами Перестановочность:
Распределительный закон умножения 3. 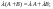 4. 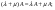 5. 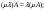 Определение5 Пусть существуют матрицы Определение5 Пусть существуют матрицы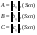 С – разность А и В, если можно записать А=В+С; обозначается С=А-В. Определение6 Пусть матрицы 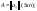  Матрица 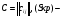 называется произведением матриц А и В (обозначается С=АВ), если называется произведением матриц А и В (обозначается С=АВ), если 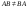 Определение7 Транспонированная матрица. Транспонировать матрицу А  значит записать столбцы матрицы А строками с теми же номерами. значит записать столбцы матрицы А строками с теми же номерами.Вопрос 2: Операция умножения матриц и ее свойства Определение6 Пусть матрицы 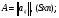 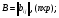 Матрица 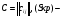 называется произведением матриц А и В (обозначается С=АВ), если называется произведением матриц А и В (обозначается С=АВ), если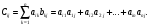  Свойства: Сочетательное свойство: Распределительное свойство: Произведение матрицы на единичную матрицу подходящего порядка равно самой матрице: Произведение матрицы на нулевую матрицу подходящей размерности равно нулевой матрице: Если и — квадратные одного и того же порядка, то произведение матриц обладает ещё рядом свойств. Умножение матриц в целом некоммутативно: Если , то матрицы и называются перестановочными или коммутирующими между собой. Определитель и след произведения не зависят от порядка умножения матриц: Билет 3. Перестановки и их четность. Изменение четности при транспозиции. Прежде чем обобщить понятие определителя на матрицы более высокого порядка, дадим некоторые новые определения.. Рассмотрим конечное множество из  элементов. Занумеруем эти элементы первыми числами натурального ряда. Таким образом, будем считать, что элементами являются числа 1, 2, … . элементов. Занумеруем эти элементы первыми числами натурального ряда. Таким образом, будем считать, что элементами являются числа 1, 2, … . . . Обычный порядок этих чисел можно изменить, переставив их. Например, числа 1,2,3 можно расположить так: 3,1,2 или 2,3,1. Всякое расположение чисел 1,2,…,  назовем перестановкой. назовем перестановкой. Утверждение. Число всех перестановок множества из  элементов равно элементов равно  !. !. Доказательство. Общий вид перестановки таков: 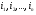 , ,где каждое из 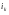 - одно из чисел - одно из чисел  , причем все они различны. В качестве , причем все они различны. В качестве 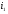 можно взять любое из можно взять любое из  чисел. Для каждого выбора числа чисел. Для каждого выбора числа 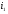 есть есть  возможность выбрать возможность выбрать  . Если . Если 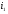 и и 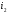 выбраны, то остается выбраны, то остается  возможности выбрать возможности выбрать 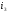 , и т.д. Итак, получаем , и т.д. Итак, получаем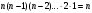 ! !способов переставить числа 1,2,… .  . Ч.т.д. . Ч.т.д.Пусть 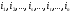 - -некоторая перестановка. Говорят, что  и и  образуют инверсию, если образуют инверсию, если  < < , но , но 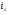 > >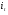 . Перестановка называется четной, если она содержит четное число инверсий, и нечетной, если число инверсий нечетно. Например: . Перестановка называется четной, если она содержит четное число инверсий, и нечетной, если число инверсий нечетно. Например:2 3 1 5 4 - 3 инверсии (2,1), (3,1).(5,4); перестановка нечетная. 4 3 1 5 2 - 6 инверсий (4,3), (4,1), (4,2), (3,1), (3,2), (5,2); перестановка четная. Установленное выше соответствие между перестановками и подстановками позволяет говорить и о четности подстановок: будем называть подстановку четной (нечетной), если соответствующая ей перестановка четная (нечетная). Знак подстановки  равен +1, если подстановка четная, и -1, если подстановка нечетная. равен +1, если подстановка четная, и -1, если подстановка нечетная.Лемма. Две перестановки 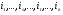 и и  имеют различную четность. Доказательство. Пусть сначала 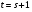 , т.е. вторая получается из первой перестановкой двух соседних элементов: , т.е. вторая получается из первой перестановкой двух соседних элементов: ; ; 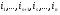 . . Инверсии, содержащиеся в первой перестановке, в которых хотя бы один элемент не равен  или или  сохраняются и во второй перестановке. Исключение составляет пара сохраняются и во второй перестановке. Исключение составляет пара 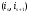 . Если она образует инверсию, то во второй перестановке пара . Если она образует инверсию, то во второй перестановке пара  инверсии не образует. И наоборот, если инверсии не было, то во второй перестановке, поменявшись местами, эти элементы образуют инверсию. Значит, количество инверсий в этих перестановках отличается на одну инверсию. инверсии не образует. И наоборот, если инверсии не было, то во второй перестановке, поменявшись местами, эти элементы образуют инверсию. Значит, количество инверсий в этих перестановках отличается на одну инверсию.Пусть теперь  и и  произвольные. Тогда вторую перестановку можно получить из первой за несколько шагов, каждый раз меняя соседние элементы: произвольные. Тогда вторую перестановку можно получить из первой за несколько шагов, каждый раз меняя соседние элементы: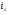 и и  , , 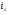 и и 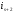 ,…, ,…,  и и 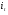 - всего - всего 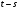 шагов; шагов;затем 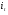 и и 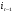 , , 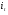 и и 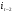 ,…, ,…, 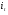 и и 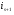 - всего - всего 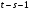 шагов. шагов.Итого, мы сделаем 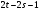 шагов. На каждом шаге знак перестановки менялся, а поскольку число шагов было нечетно, то знаки перестановок различны. шагов. На каждом шаге знак перестановки менялся, а поскольку число шагов было нечетно, то знаки перестановок различны.Утверждение Любая транспонизация элементов меняет четность перестановки. Подстановкой будем называть любое взаимно однозначное отображение множества  на себя. на себя.Билет 4. Определители 2, 3 порядков. Определние определителя порядка n. Единичная матрица и ее определитель Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:
, где М1k - определитель матрицы (детерминант), полученной из исходной матрицы вычеркиванием первой строки и k - oго столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов. \ В частности, формула вычисления определителя матрицы такова: 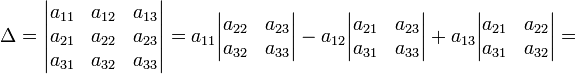 = a11a22a33 − a11a23a32 − a12a21a33 + a12a23a31 + a13a21a32 − a13a22a31 Определитель единичной матрицы равен 1 Билет 5. Неизменность определителя при транспонировании его матрицы 1.Определитель не меняется при транспонировании. Пусть А(nxn), пусть В=АT А=||a,ig|| , B=||b,gi|| a,ig = b,gi – очевидно. Рассмотрим слагаемое в detB (-1)N(P)*a£11*a£22*…*a£nn Здесь P=(1 2 … n) (£1 £2 … £n) произведение a£11*a£22*…*a£nn входит в det A со знаком P`=(£1 £2 … £n) (1 2 … n) Очевидно, что четности подстановок совпадают (-1)N(P)=(-1)N(P`) по этому det A b det B состоят из одних и тех же слагаемых произведений. 7). При транспонировании матрицы определитель не меняется: Докажем это. В разложении определителя (*) любое слагаемое с точностью до знака является произведением элементов матрицы по одному из каждой строки и из каждого столбца. Поэтому с точностью до знаков слагаемые в разложениях определителей исходной и транспонированной матриц совпадают. Теперь разберемся со знаками. Возьмем произвольное слагаемое из разложения определителя матрицы 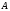 и покажем, что в разложение определителя транспонированной матрицы оно будет входить с тем же знаком. Пусть это слагаемое соответствует подстановке π: и покажем, что в разложение определителя транспонированной матрицы оно будет входить с тем же знаком. Пусть это слагаемое соответствует подстановке π:  . Упорядочим сомножители по второму индексу, т.е. по столбцам: . Упорядочим сомножители по второму индексу, т.е. по столбцам: 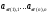 , где , где 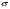 – некоторая другая подстановка, причем – некоторая другая подстановка, причем 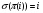 . Заметим, что количество инверсий в перестановках . Заметим, что количество инверсий в перестановках  и и 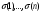 совпадает, ведь если выполнялось условие совпадает, ведь если выполнялось условие 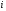 < < , но , но 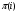 > >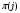 , то после упорядочивания сомножителей по номерам столбцов появится соответствующая инверсия в перестановке номеров строк. Значит, четность подстановок , то после упорядочивания сомножителей по номерам столбцов появится соответствующая инверсия в перестановке номеров строк. Значит, четность подстановок  и и 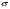 совпадает. совпадает.Билет 6. Разложение определителя в сумму определителей, если какой-либо столбец определяется суммой столбцов Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например, 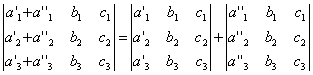 Билет 7. Свойства определителя – вынесение за знак определителя общего множителя из строки или стобца, перестановка двух строк или столбцов Ответ:.Общий множитель элементов некоторой строки можно вынести за знак определителя. Если одну из строк матрицы умножить на некоторое число 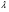 , то определитель умножится на это же число , то определитель умножится на это же число 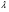 . Действительно, если все элементы одной строки умножить на . Действительно, если все элементы одной строки умножить на 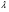 , то умножится на , то умножится на 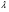 и каждое слагаемое в формуле (*), а значит, и определитель матрицы. и каждое слагаемое в формуле (*), а значит, и определитель матрицы.2). Если две строки матрицы поменять местами (элементарное преобразование типа I), то определитель матрицы поменяет знак (кососимметричность). Иначе, пусть 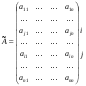 Тогда 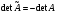 . .Доказательство. Рассмотрим произвольное слагаемое в формуле (*) для матрицы 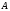 , соответствующее подстановке , соответствующее подстановке  , пока не учитывая его знак. Это слагаемое встретится и в разложении определителя , пока не учитывая его знак. Это слагаемое встретится и в разложении определителя  , но будет соответствовать другой подстановке , но будет соответствовать другой подстановке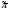 : : 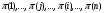 . .Согласно лемме четность подстановок  и и 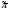 различна, а значит, различны и знаки, с которыми эти слагаемые входят в соответствующие разложения определителей. Итак, при переходе от различна, а значит, различны и знаки, с которыми эти слагаемые входят в соответствующие разложения определителей. Итак, при переходе от 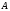 к к  все слагаемые в разложении (*) поменяют знаки, следовательно, изменит знак и определитель. все слагаемые в разложении (*) поменяют знаки, следовательно, изменит знак и определитель.Билет 8. Свойства определителя - прибавление к строке определителя другой строки, умноженной на число; прибавление линейной комбинцации 2 строк, аналогичное для столбцов. Ответ: Если к одной строке матрицы прибавить другую строку, умноженную на какое-нибудь число (элементарное преобразование типа II), то определитель матрицы не изменится. Доказательство немедленно следует из предыдущих свойств. Пусть   . .Тогда  , где , где - -матрица, у которой 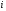 -я и -я и  -я строки совпадают, и следовательно, ее определитель равен нулю. Значит, -я строки совпадают, и следовательно, ее определитель равен нулю. Значит,  . .Определитель 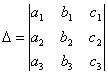 равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения. Иначе говоря, имеют место следующие равенства: , , , , , . |

 Матрицы. Операция
Матрицы. Операция