Ответ Оп Матрицей a размерности Sxn называется прямоугольная таблица из чисел, состоящая из s строк и n столбцов
 Скачать 7.71 Mb. Скачать 7.71 Mb.
|
|
Свойства решений систем линейных алгебраических уравнений Используя свойства линейных операций с матрицыми, нетрудно доказать, справедливость следующих утверждений.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы 25. Понятие о базисных и свободных неизвестных, условие нетривиальной совместности однородной системы. Система совместна – если имеет хотябы одно решение. Несовместна – если не имеет ни одного решениия Система линейных алгеьраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы. Если система совместна, найти какой-либо базисный минор порядка r(минор, порядок которого определяет ранг матрицы, называется ранг матриц). Взять r уравнений из коэффицентов которых составлен базисный минор(остальные уравнения отбросить). Неизвестные которые входят в базисный минор называются главными, и оставляются слева, а оставшиеся назыаются свободные, и переносятся вправо 26. Понятие о линейной зависимости решений; существование фундаментальной системы решений . Пусть дана однородная система линейных уравнений 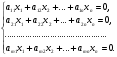 (*) (*)Предположим, что набор чисел 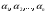 - какое-то решение этой системы. Тогда набор чисел - какое-то решение этой системы. Тогда набор чисел 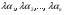 тоже является решением. Это проверяется непосредственной подстановкой в уравнения системы. Далее, если набор тоже является решением. Это проверяется непосредственной подстановкой в уравнения системы. Далее, если набор 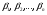 - некоторое другое решение, то - некоторое другое решение, то 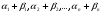 тоже является решением: тоже является решением: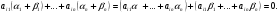 И вообще, любая линейная комбинация решений системы (*) является решением этой системы. Всякий базис в множестве Q состоит из n – r векторов e1,...,en-r. Соответствующая ему в каноническом базисе система вектор-столбцов Е1,..., Еn–r наз. фундаментальной системой решений. К примеру у нас было 4 неизвестных, 2 базисных, 2 свободных. X3,x4 заменяем на c1 и с2. Как пример ответ: ( ¾ - 1/4с1+7/4с2) ½ + 3/2c1-1/2c2 C1 C2 Базисные решения Е1,..., Еn–r могут быть получены по правилу Крамера, если свободным неизвестным придавать пооче редно значение 1, полагая остальные равными 0. 27. Выражение базисных через свободные Если система совместна, найти какой-либо базисный минор порядка r(минор, порядок которого определяет ранг матрицы, называется ранг матриц). Взять r уравнений из коэффицентов которых составлен базисный минор(остальные уравнения отбросить). Неизвестные которые входят в базисный минор называются главными, и оставляются слева, а оставшиеся назыаются свободные, и переносятся вправо. После чего выражаем базисные через свободные. Как пример: Получена система 2x1+x2=2+x3+3x4 ; 4x1 = 3-x3+7x4 у нас было 4 неизвестных, 2 базисных, 2 свободных. X3,x4 заменяем на c1 и с2. Как пример ответ: ( ¾ - 1/4с1+7/4с2) ½ + 3/2c1-1/2c2 C1 C2 28. Понятие обшего решения одногородной системы, теорема об общем решении Однородная система: АX=0. Неоднородная AX=B Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т.е. r Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю  Определяем ранг матрицы. Базисный минор – из него черпаем именно те неизвестные. Остальные неизвестные заменяем на c1…cn. Затем выписываем общее решение, и делаем фундаменталку – т.е. если у нас 3 c1 c2 c3, в каждом решении чередуем 1 и 0 – (x1,x2,1,0,0), (x1,x2,0,1,0) 29.
Решим систему 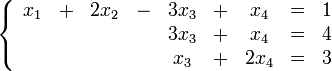 Преобразуем её к 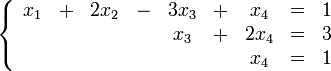 Тогда переменные и обязательно будут главными, возьмём также в качестве главной. Заметим, что является частным решением. Составим однородную систему: 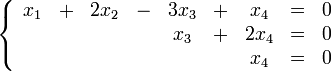 Тогда, подставив единицу в качестве свободной переменной , получим ФСР однородной системы: 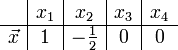 Общее решение системы может быть записано так: 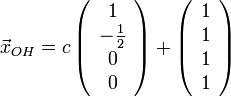 30 МЕТОД ГАУССА 15. Исследование систем линейных алгебраических уравнений методом Гаусса. Эффективным методом решения и исследования систем линейных уравнений является метод последовательного исключения неизвестных путем элементарных преобразований. - метод Гаусса. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему (имеющей такие же решения) специального вида, которая легко исследуется и решается. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе. Применим данный метод для решения системы 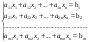 Пусть в системе (1.7) а110. Этого можно добиться несколькими способами в числе которых перестановка уравнений местами, элементарные преобразования над строками. Все преобразования в дальнейшем будем проводить с расширенной матрицей. Нужно исключить все коэффициенты при х1, т.е. обратить все элементы первого столбца, начиная со второй строки в 0. Разделим первую строку на а11, т.е. преобразуем систему в равносильную так, чтобы а11=1. Единственное условие, которое должно быть выполнено при выборе, состоит в том, что коэффициент при избранном неизвестном должен быть не равен 0. x1+ 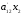 +...+ +...+ 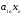 = =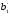 (1.10) (1.10)Исключим теперь х1 из остальных уравнений системы. Будем умножать (1.8) последовательно на а21, а31,..., аn1 и вычитать соответственно из 2-го, 3-го и последнего уравнений системы. После этого система уравнений (1.7), заменится эквивалентной системой. 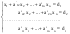 (1.11) (1.11)Эти уравнения также образуют систему n уравнений с неизвестными х1,...,хn. Порядок ее тот же, что и у исходной системы. К ней можно применить такое же преобразование. Выбрать второе уравнение, коэффициент при х2 привести к 1, исключить х2 из остальных уравнений и т.д. Такие преобразования проводятся до тех пор, пока они возможны, т.е. либо мы переберем все уравнения системы, либо когда в оставшихся уравнения не будет коэффициентов не равных 0. В результате получаем систему ступенчатого вида: 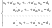  (1.12) (1.12)Возможны 3 случая. Получаем строку вида: 0+0+0+...+0=dr. В этом случае решений нет. annxn=bn В этом случае единственное решение. 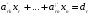 - бесчисленное множество решений. - бесчисленное множество решений.Пример Решить систему линейных алгебраических уравнений методом Гаусса.   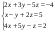  Запишем расширенную матрицу системы: Запишем расширенную матрицу системы: 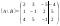 . .Нужно преобразовать данную матрицу таким образом, чтобы а11=1. Для этого можно разделить первую строку матрицы на 2. А можно переставить местами 1-ю и 2-ю строки, тогда получим а11=1.  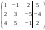 . .Умножаем первую строку матрицы последовательно на (-2), (-4) и складываем соответственно со второй и третьей строками, получаем:  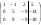 . .В полученной матрице 2-ю строку нужно разделить на 5, для того чтобы а22=1. В данном примере проще провести следующие эквивалентные преобразования: 3-ю строку разделить на 9, и переставить местами 2-ю и 3-ю строки. Получим:  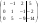 . .Теперь умножаем 2-ю строку на (-5) и прибавляем к третьей строке:  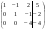 . .Получили матрицу ступенчатого вида. Третьей строке соответствует уравнение: -4z=-4. Откуда получаем z=1. Второй строке соответствует уравнение: y-z=-2. Получаем, что у= -1. И, наконец, первой строке соответствует уравнение: x-y+2z=5. Откуда х=2. 31.Векторы в пространстве, линейные операции над ними и их свойства. Линейные операции над векторами  Опр1: Вектор Опр1: Вектор 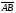 - направленный отрезок. - направленный отрезок. A – начало, В – конец.Если А=В  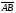 = =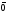 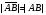 1)Коллинеарные векторы – лежащие на одной прямой или на || прямых;  2) 2)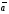 , , 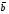 , ,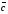 - компланарные, если будучи приведены к одному началу лежат в одной плоскости; - компланарные, если будучи приведены к одному началу лежат в одной плоскости;3) 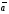 = =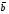 , если а)| , если а)|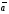 |=| |=|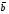 |;б) |;б) 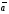  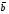 Опр2:Суммой векторов 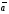 , ,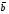 назовем вектор назовем вектор 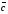 , такой что: , такой что:Опр3:Произведением 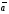 на вещественно число на вещественно число 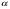 назовем назовем 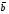 : :1)| 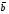 |= |=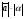 2) 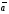  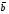 , , 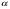 >0 >0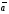 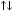 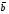 , ,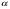 <0 <0Утв:Множество векторов(направленных отрезков) с операциями 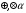 , введенными в опр2 и опр3, есть линейное пространство. , введенными в опр2 и опр3, есть линейное пространство.Свойства линейных операций над векторами: 1) 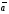 + +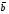 = =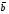 + +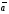 2) ( 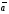 + +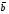 )+ )+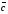 = =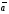 +( +(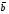 + +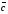 ) )3) ( 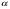 + +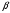 ) )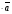 = =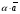 + +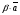 4) 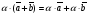 5) 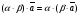 6) 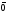 : : 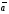 + +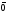 = =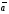 7) 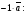 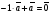 8) 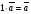 Опр4: 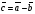 если если 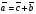 Длинна вктора = x2+y2+z2 в корне 32. Базисы на прямой, на плоскости и в пространстве Базисы на прямой, на плоскости, в пространстве. Опр1. Вектор 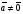 , , 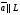 называется базисом на прямой L, если называется базисом на прямой L, если 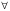 вектор вектор 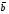 , ,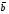 ||L может быть записан в виде ||L может быть записан в виде 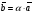 Опр2.Два линейно независимых вектора 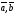 , лежащие в плоскости P, называются базисом на плоскости Р, если , лежащие в плоскости P, называются базисом на плоскости Р, если 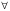 вектор вектор 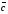 , лежащий на плоскости Р можно записать в виде , лежащий на плоскости Р можно записать в виде 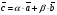 . .Опр3.Три линейно независимых вектора 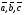 называются базисом в пространстве, если называются базисом в пространстве, если 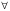 вектор вектор 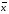 может быть записан в виде может быть записан в виде 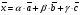 Теорема Любой ненулевой вектор 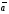 , ,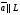 образует базис на прямой L. образует базис на прямой L.Любая пара неколлинеарных векторов 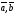 , лежащих в плоскости Р образует базис на плоскости Р , лежащих в плоскости Р образует базис на плоскости РЛюбая тройка некомпланарых векторов 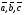 образует базис в пространстве. образует базис в пространстве.Док-во: самостоятельно (1) 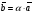 на прямой на прямой(2) 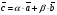 на плоскости на плоскости(3) 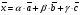 в пространстве в пространствеОпр4 Правые части формул (1),(2),(3) называются разложением векторов 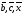 по базисам по базисам 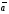 ; ;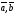 ; ;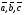 соответственно, числа соответственно, числа 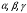 соответственными координатами. соответственными координатами.Теорема1:Разложение по базису единственно(самостоятельно!) Теорема2:При сложении векторов их соответственные координаты складываются. При умножении вектора на число его координаты умножаются на это число |
