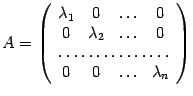Ответ Оп Матрицей a размерности Sxn называется прямоугольная таблица из чисел, состоящая из s строк и n столбцов
 Скачать 7.71 Mb. Скачать 7.71 Mb.
|
|
51(2 ЛИСТА!!!!!!!!!). Линейная независимость собственных векторов. Теорема о матрице линейного оператора в базисе из собственных векторов. Оператор простой структуры Теорема. Пусть собственные значения 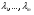 оператора различны. Тогда отвечающие им собственные векторы линейно независимы. оператора различны. Тогда отвечающие им собственные векторы линейно независимы.Доказательство проведем методом математической индукции по количеству векторов. Для одного собственного вектора утверждение теоремы очевидно. Предположим, что утверждение теоремы верно для 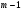 векторов векторов 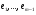 . Добавим к этим векторам еще один вектор . Добавим к этим векторам еще один вектор 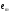 . Предположим, что эта система из . Предположим, что эта система из 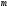 векторов линейно зависима, т.е. существуют числа векторов линейно зависима, т.е. существуют числа 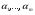 , одновременно не равные нулю, такие, что , одновременно не равные нулю, такие, что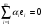 . (*) . (*)Применим к обеим частям равенства оператор : 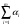 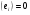 . .Так как векторы 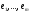 - собственные, отвечающие различным собственным значениям - собственные, отвечающие различным собственным значениям 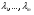 , то: , то: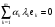 . (**) . (**)Вычтем из равенства (**) равенство (*), умноженное на 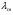 : :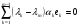 . .Так как все числа 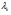 различны, то из линейной независимости векторов различны, то из линейной независимости векторов 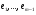 следует равенство нулю коэффициентов следует равенство нулю коэффициентов 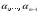 . Но тогда из равенства (*) следует, что . Но тогда из равенства (*) следует, что 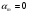 . Это означает, что векторы . Это означает, что векторы 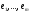 линейно независимы. Теорема доказана. линейно независимы. Теорема доказана. Следствие. Если характеристический многочлен линейного оператора имеет 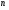 различных корней, то существует базис, в котором матрица этого оператора имеет диагональный вид. различных корней, то существует базис, в котором матрица этого оператора имеет диагональный вид.Действительно, если характеристический многочлен оператора имеет ровно 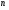 различных корней, то оператор имеет различных корней, то оператор имеет 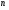 различных собственных значений. Этим собственным значениям соответствуют различных собственных значений. Этим собственным значениям соответствуют 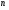 собственных векторов, причем они линейно независимы. Возьмем их в качестве базисных. Очевидно, в таком базисе матрица оператора будет диагональной, собственных векторов, причем они линейно независимы. Возьмем их в качестве базисных. Очевидно, в таком базисе матрица оператора будет диагональной,Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид  где Теорема 19.2 Пусть -- линейное преобразование -мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид
тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования , соответствующими собственным числам . Доказательство. Пусть преобразование имеет линейно независимых собственных векторов , соответствующих собственным числам . Так как векторы линейно независимы, то они образуют базис. Найдем матрицу преобразования в этом базисе. Ее первый столбец является координатным столбцом вектора . Так как -- собственный вектор, то Координатный столбец этого вектора Координатный столбец этого вектора Пусть в некотором базисе матрица линейного преобразования имеет вид (19.5). Найдем образ вектора . Этот вектор имеет координатный столбец 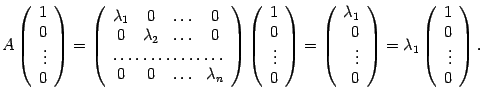 Следовательно, -- собственное число преобразования , а -- соответствущий ему собственный вектор. Аналогично находим, что любой базисный вектор является собственным вектором преобразования , соответствующим собственному числу . Следствие 19.2 Если у матрицы порядка существует набор из линейно независимых собственнных векторов, соответствующих собственным числам , то матрица подобна диагональной матрице с числами на диагонали. 52(2 ЛИСТА). Понятие евклидова пространства.Аксиомы. Неравенство Коши-Буняковского Если каждой паре векторов
то говорят, что в линейном пространстве определено скалярное произведение Определение. Линейное пространство E называется евклидовым,если в нем определено скалярное произведение. 16.3. Неравенство Коши - Буняковского. Теорема. Для любых векторов 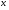 и и 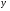 справедливо неравенство справедливо неравенство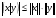 . .Доказательство. Так как скалярное произведение является положительно определенной формой, то 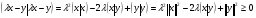 . .При фиксированных векторах 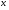 и и 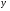 мы имеем квадратный трехчлен от мы имеем квадратный трехчлен от 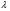 , дискриминант которого отрицательный или равен нулю: , дискриминант которого отрицательный или равен нулю: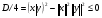 . .Отсюда 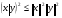 или или 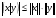 . Теорема доказана. . Теорема доказана. Следствие (неравенство треугольника). Для любых векторов 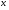 и и 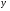 справедливо неравенство справедливо неравенство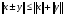 . .Доказательство. 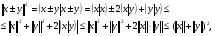 следовательно, 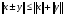 . .Пусть дано линейное пространство L со скалярным произведением . Пусть — норма, порождённая скалярным произведением, то есть Евклидово пространство (в математике), пространство, свойства которого описываются аксиомами евклидовой геометрии. В более общем смысле Е. п. называется n-мepное векторное пространство, в котором возможно ввести некоторые специальные координаты (декартовы) так, что метрика его будет определена следующим образом: если точка М имеет координаты (х1, х2,..., xn), а точка М* — координаты (x1*, x2*,..., xn*), то расстояние между этими точками
53. Евклидово пространства: Примеры, неравенство треугольника\ Наглядными примерами евклидовых пространств могут служить пространства:
Можно привести и несколько более абстрактные примеры:
54. Ортогональность векторов. Процесс ортогонализации Шмидта. Существование ортонормированного базиса в Евклидовом пространстве Определение. Векторы 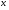 и и 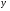 называются ортогональными, если угол между ними равен называются ортогональными, если угол между ними равен 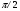 , т.е. , т.е. 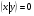 . .Нулевой вектор ортогонален любому вектору. Заметим, что из ортогональности векторов 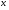 и и 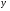 следует теорема Пифагора: следует теорема Пифагора: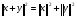 . .Эту теорему можно обобщить на любое число попарно ортогональных векторов: 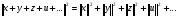 Процесс: Процесс Грама(англ.) ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе строится ортогональная система такая, что каждый вектор bi линейно выражается через , то есть матрица перехода от {ai} к {bi} ― верхнетреугольная матрица. При этом можно добиться того, чтобы система {bi} была ортонормированной и чтобы диагональные элементы матрицы перехода были положительны; этими условиями система {bi} и матрица перехода определяются однозначно. 16.6. Процесс ортогонализации Грама – Шмидта. Пусть 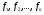 - произвольный базис евклидова пространства. Мы будем строить новый – ортонормированный – базис пространства - произвольный базис евклидова пространства. Мы будем строить новый – ортонормированный – базис пространства 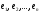 . . В качестве первого вектора нового базиса возьмем вектор 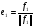 . Таким образом, длина вектора . Таким образом, длина вектора 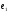 равна 1. Прежде, чем построить второй вектор нового базиса, построим вектор равна 1. Прежде, чем построить второй вектор нового базиса, построим вектор 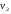 : :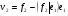 . .Вектор 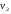 не может быть нулевым, поскольку векторы не может быть нулевым, поскольку векторы 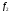 и и 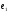 линейно независимы. Заметим, что векторы линейно независимы. Заметим, что векторы 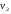 и и 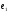 ортогональны. В качестве второго базисного вектора возьмем вектор ортогональны. В качестве второго базисного вектора возьмем вектор 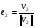 . Теперь будем строить третий базисный вектор. Сначала возьмем вектор . Теперь будем строить третий базисный вектор. Сначала возьмем вектор 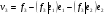 . .Этот вектор – ненулевой, так как векторы 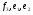 линейно независимы,- ортогонален векторам линейно независимы,- ортогонален векторам 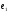 и и 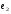 . Остается только нормировать его: . Остается только нормировать его: 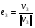 . Алгоритм ясен: имея . Алгоритм ясен: имея 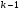 вектор нового базиса, мы построим сначала вектор вектор нового базиса, мы построим сначала вектор 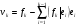 . .Этот вектор ненулевой и ортогональный векторам 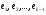 . Нормировав его, получаем . Нормировав его, получаем 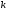 -й вектор нового базиса -й вектор нового базиса 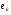 . .Теорема. В произвольном n-мерном евклидовом пространстве существует ортонормированный базис. 55. Ортонормированные базисы и их свойства Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат. |