Ответ Оп Матрицей a размерности Sxn называется прямоугольная таблица из чисел, состоящая из s строк и n столбцов
 Скачать 7.71 Mb. Скачать 7.71 Mb.
|
|
40. Общее уравнение плоскости и уравнение плоскости в отрезках Плоскость P в декартовой прямоугольной системе координат 0xyz может быть задана уравнением одного из следующих видов Аx+By+Cz+D=0 – общее уравнение плоскости 11.1 Общее уравнение плоскости. Зафиксируем декартову прямоугольную систему координат. Рассмотрим произвольное уравнение первой степени 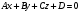 . (*) . (*)Заметим, что хотя бы один из коэффициентов 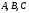 не равен нулю (иначе это уравнение имело бы нулевую степень). Тогда уравнение (*) имеет хотя бы одно решение не равен нулю (иначе это уравнение имело бы нулевую степень). Тогда уравнение (*) имеет хотя бы одно решение 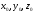 , т.е. существует хотя бы одна точка, координаты которой удовлетворяют уравнению (*): , т.е. существует хотя бы одна точка, координаты которой удовлетворяют уравнению (*):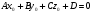 . (**) . (**)Вычтем из уравнения (*) уравнение (**): 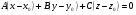 . (***) . (***)Уравнение (***) эквивалентно уравнению (*), т.е. если координаты точки удовлетворяют уравнению (*), то они удовлетворяют уравнению (***), и наоборот. Обозначим 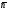 вектор с координатами вектор с координатами 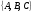 . Пусть . Пусть 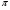 - плоскость, проходящая через точку - плоскость, проходящая через точку 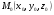 и перпендикулярная вектору и перпендикулярная вектору 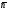 . Если точка . Если точка 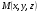 лежит в плоскости лежит в плоскости 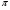 , то вектор , то вектор 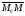 перпендикулярен вектору перпендикулярен вектору 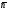 , скалярное произведение этих векторов равно 0. Тогда координаты точки , скалярное произведение этих векторов равно 0. Тогда координаты точки 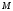 удовлетворяют уравнению (***) и, следовательно, уравнению (*). Если же точка удовлетворяют уравнению (***) и, следовательно, уравнению (*). Если же точка 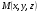 не лежит в плоскости не лежит в плоскости 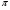 , то векторы , то векторы 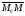 и и 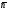 не перпендикулярны, и скалярное произведение этих векторов не равно 0. Значит, в этом случае координаты точки не перпендикулярны, и скалярное произведение этих векторов не равно 0. Значит, в этом случае координаты точки 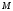 не удовлетворяют уравнению (***) и уравнению (*). не удовлетворяют уравнению (***) и уравнению (*).Пусть теперь дана произвольная плоскость. Выберем вектор 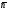 , перпендикулярный этой плоскости, и произвольную точку , перпендикулярный этой плоскости, и произвольную точку 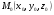 , лежащую в этой плоскости. Если , лежащую в этой плоскости. Если 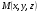 произвольная точка плоскости, то векторы произвольная точка плоскости, то векторы 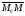 и и 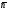 перпендикулярны, их скалярное произведение равно 0. Тогда координаты точки удовлетворяют уравнению (***) и, следовательно, уравнению (*), являющимся уравнением первой степени. Мы доказали перпендикулярны, их скалярное произведение равно 0. Тогда координаты точки удовлетворяют уравнению (***) и, следовательно, уравнению (*), являющимся уравнением первой степени. Мы доказалиУтверждение. Произвольная плоскость в пространстве определяется уравнением первой степени. Обратно, любое уравнение первой степени определяет в пространстве плоскость. Уравнение (*) называется общим уравнением плоскости. 11.3. Уравнение плоскости в отрезках. Общее уравнение плоскости (*) называется полным, если все коэффициенты 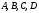 отличны от нуля. В противном случае оно называется неполным. Неполные уравнения задают плоскость, проходящую через начало координат, параллельную какой-либо координатной оси или параллельную какой-либо координатной плоскости. Все эти случаи несложно рассмотреть. отличны от нуля. В противном случае оно называется неполным. Неполные уравнения задают плоскость, проходящую через начало координат, параллельную какой-либо координатной оси или параллельную какой-либо координатной плоскости. Все эти случаи несложно рассмотреть.Мы же рассмотрим полное уравнение плоскости. Так как все коэффициенты общего уравнения отличны от нуля, его можно переписать в виде: 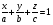 , ,где 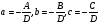 . . Этот вид уравнения плоскости называется уравнением плоскости в отрезках. 41. Взаимное расположение двух плоскостей. Возможны два случая взаимного расположения двух плоскостей в пространстве:
Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в противном случаи они пересекаются. Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Доказательство: Пусть и - данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в плоскости . Допустим, что плоскости и не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД. Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым. Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. Доказательство: Пусть - плоскость, в -перпендикулярная ей прямая, - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости и . Докажем, что плоскости и перпендикулярны. Проведем в плоскости через точку пересечения прямой в с плоскостью прямую а, перпендикулярную прямой с. Проведем через прямые а и в плоскость . Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости и перпендикулярны. ч.т.д. 42. Нормальное уравнение плоскости и его свойства
в векторной форме: где - единичный вектор, — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель (знаки и противоположны).  43. Уравнения прямой линии в пространстве: Общие уравнения, каноничекие и параметрические уравнения. Канонические уравнения: Выведем уравнение прямой, проходящей через данную точку 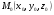 и параллельную данному направляющему вектору и параллельную данному направляющему вектору 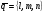 . Заметим, что точка . Заметим, что точка 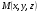 лежит на этой прямой тогда и только тогда, когда векторы лежит на этой прямой тогда и только тогда, когда векторы 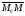 и и 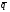 коллинеарны. Это означает, что координаты этих векторов пропорциональны: коллинеарны. Это означает, что координаты этих векторов пропорциональны: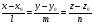 . .Эти уравнения называют каноническими. Заметим, что одна или две координаты направляющего вектора могут оказаться равными нулю. Но мы воспринимаем это как пропорцию: 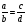 мы понимаем как равенство мы понимаем как равенство 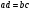 . .Общие уравнения: (A1x+B1y+C1z+D1=0 (A2x+B2y+C2z+D2=0 Где коэффиценты А1-С1 не пропорциональны A2-C2,что равносильно ее заданию как линии пересечения плоскостей Параметрические: Откладывая от точки 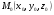 векторы векторы 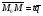 для различных значений для различных значений 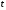 , коллинеарные направляющему вектору, мы будем получать на конце отложенных векторов различные точки нашей прямой. Из равенства , коллинеарные направляющему вектору, мы будем получать на конце отложенных векторов различные точки нашей прямой. Из равенства 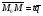 следует: следует: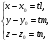 или 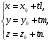 Переменную величину 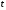 называют параметром. Поскольку для любой точки прямой найдется соответствующее значение параметра и поскольку различным значениям параметра соответствуют различные точки прямой, то существует взаимно однозначное соответствие между значениями параметра и точками прямой. Когда параметр называют параметром. Поскольку для любой точки прямой найдется соответствующее значение параметра и поскольку различным значениям параметра соответствуют различные точки прямой, то существует взаимно однозначное соответствие между значениями параметра и точками прямой. Когда параметр 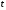 пробегает все действительные числа от пробегает все действительные числа от 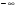 до до 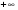 , соответствующая точка , соответствующая точка 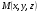 пробегает всю прямую. пробегает всю прямую. 44. Понятие линейного пространства. Аксиомы. Примеры линейных пространств Пример линейного пространства – множество всех геометрических векторов. Линейное, или векторное пространство над полем P — это непустое множество L, на котором введены операции сложения, то есть каждой паре элементов множества ставится в соответствие элемент того же множества, обозначаемый и умножения на скаляр (то есть элемент поля P), то есть любому элементу и любому элементу ставится в соответствие элемент из , обозначаемый При этом на операции накладываются следующие условия: , для любых (коммутативность сложения); существует такой элемент , что для любого (существование нейтрального элемента относительно сложения), в частности L не пусто; для любого существует такой элемент , что (существование противоположного элемента). (умножение на нейтральный (по умножению) элемент поля P сохраняет вектор). Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы. Простейшие свойства Векторное пространство является абелевой группой по сложению. Нейтральный элемент является единственным, что вытекает из групповых свойств. для любого . Для любого противоположный элемент является единственным, что вытекает из групповых свойств. для любого . для любого . Элементы линейного пространства называются векторами. Пространство называется действительным, если в нем оперция умножения векторов на число определена только для действительных числе, и комплексным, если эта оперкция определана только для комплексных чисел. 45. Базис и размерност линейного прорстранства, связь между ними. Конечная сумма вида называется линейной комбинацией элементов Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля. Элементы называются линейно зависимыми, если существует их нетривиальная линейная комбинация, равная θ. В противном случае эти элементы называются линейно независимыми. Бесконечное подмножество векторов из L называется линейно зависимым, если линейно зависимо его некоторое конечное подмножество, и линейно независимым, если любое его конечное подмножество линейно независимо. Число элементов (мощность) максимального линейно независимого подмножества пространства не зависит от выбора этого подмножества и называется рангом, или размерностью, пространства, а само это подмножество — базисом (базисом Га́меля или линейным базисом). Элементы базиса также называют базисными векторами. Свойства базиса: Любые n линейно независимых элементов n-мерного пространства образуют базис этого пространства. Любой вектор можно представить (единственным образом) в виде конечной линейной комбинации базисных элементов:  46. Координты вектора в данном базисе. Линейные операции с векторами в координатной форме п.4. Линейные операции с векторами в координатной форме записи. Пусть – базис пространства и – два его произвольных вектора. Пусть и – запись этих векторов в координатной форме. Пусть, далее, – произвольное действительное число. В этих обозначениях имеет место следующая теорема. Теорема. (О линейных операциях с векторами в координатной форме.) 1) ; 2) . Пусть Ln – произвольное n-мерное пространство, B = (e1,….,en) - фиксированный базис в нем. Тогда всякому вектору x пренадлежащему Ln взаимно однозначно соответствует столбец его координат в этом базисе. X = x1e1+….xnen X = (X1 …. XN) 47Переход к новому базису. М атрица перехода. Преобразование координат вектора при переходе к новому базису.  48. Линейные операторы в линейном пространстве. Матрица оператора и ее использование при осуществлении действия оператора.  49. Преобразование матрицы оператора при переходе к новому базису 13.4. Изменение матрицы линейного отображения при замене базисов. Посмотрим, как изменится матрица линейного отображения, если в пространствах 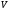 и и 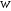 перейти к новым базисам. Пусть перейти к новым базисам. Пусть 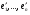 и и 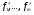 - новые базисы. Обозначим через - новые базисы. Обозначим через 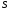 матрицу перехода от матрицу перехода от 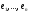 к к 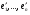 , через , через 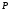 - матрицу перехода от - матрицу перехода от 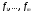 к к 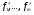 . Тогда: . Тогда: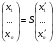 , , 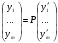 . .Подставим в равенство (*): 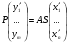 . .Отсюда 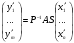 . .Значит, при изменении базисов матрица 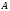 отображения преобразуется в матрицу отображения преобразуется в матрицу 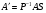 . .В случае, когда линейное отображение является линейным оператором, вместо пары базисов мы имеем один базис в пространстве 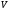 . Тогда при замене этого базиса матрица оператора преобразуется по формуле . Тогда при замене этого базиса матрица оператора преобразуется по формуле 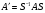 . .Сканировать 129  50. Собственные векторы и собственные значения линейного оператора. Характерестический многочлен и его независимость от выбора базиса. 14.2. Собственные векторы и собственные значения оператора. Попробуем решить задачу нахождения одномерных подпространств, инвариантных относительно оператора . Определение. Пусть 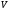 - вещественное (комплексное) линейное пространство. Ненулевой вектор - вещественное (комплексное) линейное пространство. Ненулевой вектор 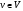 называется собственным вектором оператора , если называется собственным вектором оператора , еслидля некоторого 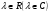 . При этом число . При этом число 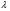 называется собственным значением оператора . называется собственным значением оператора .Обозначим 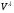 множество всех векторов множество всех векторов 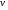 из из 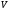 , для которых выполняется равенство , для которых выполняется равенство 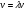 . Заметим, что если . Заметим, что если 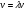 и и 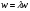 , то , то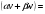     . .Легко видеть, что  является инвариантным подпространством, его ненулевые векторы являются собственными, отвечающими собственному значению является инвариантным подпространством, его ненулевые векторы являются собственными, отвечающими собственному значению  . .Если вектор  является собственным, отвечающим собственному значению является собственным, отвечающим собственному значению  , то выполняется равенство , то выполняется равенство 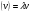 , откуда . Это означает, что ядро оператора нетривиально, следовательно, равен 0 определитель этого оператора. Зафиксируем базис пространства. Если в этом базисе матрица оператора равна , откуда . Это означает, что ядро оператора нетривиально, следовательно, равен 0 определитель этого оператора. Зафиксируем базис пространства. Если в этом базисе матрица оператора равна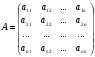 , ,то равенство нулю определителя оператора запишется в виде: 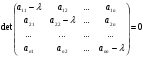 . .Представив определитель как сумму произведений элементов матрицы (по определению), мы получим равенство, в левой части которого стоит многочлен степени 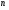 от от 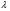 : :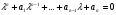 . Определение. Многочлен . Определение. Многочлен 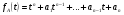 называется характеристическим многочленом матрицы называется характеристическим многочленом матрицы 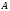 Пусть L — линейное пространство над полем K, — линейное преобразование. Собственным вектором линейного преобразования A называется такой ненулевой вектор , что для некоторого Ax = λx Собственным значением линейного преобразования A называется такое число , для которого существует собственный вектор, то есть уравнение Ax = λx имеет ненулевое решение . Упрощённо говоря, собственный вектор - любой ненулевой вектор x, который отображается оператором в коллинеарный λx, а соответствующий скаляр λ называется собственным значением оператора. Собственным подпространством линейного преобразования A для данного собственного числа называется множество всех собственных векторов , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его Eλ. По определению, где E — единичный оператор. |
