Ответ Оп Матрицей a размерности Sxn называется прямоугольная таблица из чисел, состоящая из s строк и n столбцов
 Скачать 7.71 Mb. Скачать 7.71 Mb.
|
|
Теорема. В любом конечномерном пространстве существует ортонормированный базис. Доказательство теоремы немедленно следует из того, что существует базис 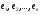 , в котором квадратичная форма, соответствующая скалярному произведению, имеет канонический вид , в котором квадратичная форма, соответствующая скалярному произведению, имеет канонический вид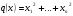 , ,( 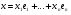 ). В этом базисе скалярное произведение векторов ). В этом базисе скалярное произведение векторов 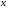 и и 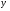 задается формулой задается формулой 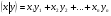 . Но это и означает, что базис . Но это и означает, что базис 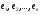 ортонормированный. ортонормированный.Свойства: в ортонормированном базисе скалярное произведение векторов равно сумме произведений одноименных координат этих векторов. Любую ортонормированную систему векторов конечномерного евклидова пространства можно дополнить до ортонормированного базиса. 56.Квадратичные формы. Приведение квадратичной формы к каноническому виду методом Лангаржа.    57. Положительно определенные квадратичные формы. Критерий Сильвестра Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой. Пусть квадратичная форма имеет в каком-то базисе матрицу 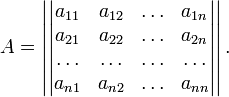 Тогда эта форма положительно определена, если и только если все её главные (угловые) миноры Δi положительны. Форма отрицательно определена, если и только если знаки Δi чередуются, причём Δ1 < 0. Здесь главными минорами матрицы A называются определители вида 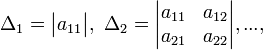  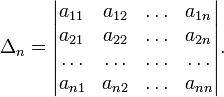 Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица 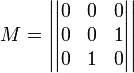 не является неотрицательно определённой — так как, например, (Mv,v) = − 2 для v = (0,1, − 1). В то же время все её главные миноры равны 0, то есть неотрицательны. Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны. 58.Кривые второго порядка: Канонические уравнения и форма: Эллипс   Эллипс, его фокусы и главные оси Гипербола 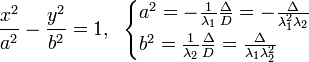 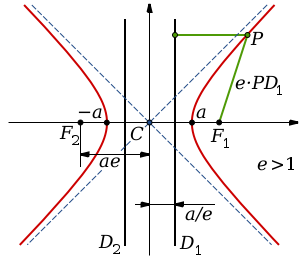 Асимптоты гиперболы (красные кривые), показанные голубым пунктиром, пересекаются в центре гиперболы, C. Два фокуса гиперболы обозначены как F1 и F2. Директрисы гиперболы обозначены линиями двойной толщины и обозначены D1 и D2. Эксцентриситет ε равен отношению расстояний точки P на гиперболе до фокуса и до соответствующей директрисы (показаны зеленым). Вершины гиперболы обозначены как ±a. Парабола  59. Поверхности второго порядка Эллиптический цилиндр: 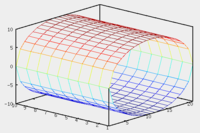 Параболический цилиндр: 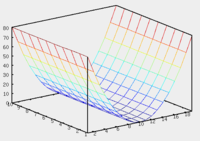 Гиперболический цилиндр: 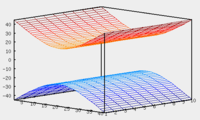 Эллипсоид: Однополостной 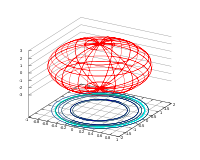 гиперболоид: 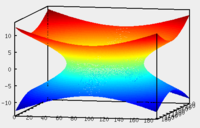 Двуполостной гиперболоид: 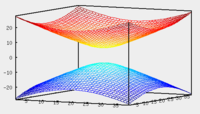 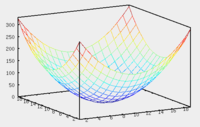 60. Комплексные числа: Сложение, вычитание, умножение и деление в алгебраической форме 1. Понятие комплексного числа. Из школьного курса математики известно, что действительных чисел недостаточно для решения квадратных уравнений. Простейшее из квадратных уравнений 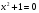 не имеет корней среди действительных чисел. Попробуем расширить систему действительных чисел до такой системы чисел, чтобы это уравнение имело решение. не имеет корней среди действительных чисел. Попробуем расширить систему действительных чисел до такой системы чисел, чтобы это уравнение имело решение.Выберем на плоскости прямоугольную систему координат с осью абсцисс 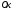 и осью ординат и осью ординат 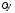 . Будем обозначать . Будем обозначать 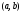 точку с абсциссой точку с абсциссой 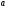 и ординатой и ординатой 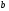 . Определим на множестве точек плоскости (другими словами, на упорядоченных парах действительных чисел) операции сложения и умножения следующим образом: . Определим на множестве точек плоскости (другими словами, на упорядоченных парах действительных чисел) операции сложения и умножения следующим образом: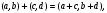 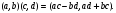 Заметим, что 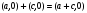 , ,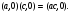 Поэтому точки, лежащие на оси 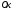 можно считать точками действительной оси, и мы не будем различать точку можно считать точками действительной оси, и мы не будем различать точку 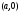 и действительное число и действительное число 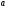 . .Кроме того, 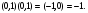 Традиционно эту точку обозначают буквой 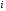 . .Учитывая, что для 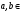 R R 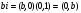 и и 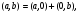 получаем: получаем: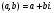 В этой записи операции сложения и умножения выглядят так: 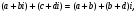 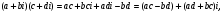 т.е. эти операции выполняются как с обычными двучленами с учетом равенства 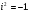 Пусть дано число 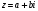 . Назовем число . Назовем число 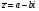 сопряженным числу сопряженным числу  . Заметим, что . Заметим, что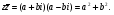 Определив операции сложения и умножения, естественно ввести обратные операции вычитания и деления: 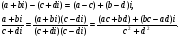 Последняя формула довольно громоздка, и запоминать ее не стоит. Следует только знать, что для вычисления дроби нужно числитель и знаменатель умножить на сопряженное знаменателю число. Итак, построенная система чисел с алгебраическими операциями называется множеством комплексных чисел и обозначается С. Ко́мпле́ксные[1] чи́сла — расширение множества вещественных чисел. обычно обозначается . Каждое комплексное число z представляет собой сумму x + iy, где x и y вещественные, а i это так называемая мнимая единица, являющейся корнем уравнения i2 = − 1 Множество комплексных чисел обозначается в литературе как (ажурное), а иногда как C (простое), (полужирное). 61. Тригонометрическая форма комплексного числа Возведение в степень и извлечение корня из комплексного числа(2 СТРАНИЦЫ) 2. Тригонометрическая форма записи комплексного числа. Форма записи комплексного числа 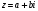 называется алгебраической. Число называется алгебраической. Число 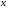 называется действительной частью комплексного числа называется действительной частью комплексного числа  , , 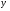 - мнимой частью. Обозначение: - мнимой частью. Обозначение: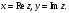 Кроме этой формы существует другая – тригонометрическая. Сначала введем некоторые понятия. Модулем комплексного числа называется неотрицательное действительное число 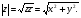 Геометрический смысл модуля прост – это расстояние от начала координат до точки плоскости, соответствующей комплексному числу  . .Аргументом 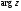 комплексного числа комплексного числа  называют угол между положительным направлением оси называют угол между положительным направлением оси 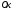 и радиус-вектором точки и радиус-вектором точки  (отсчитываемый в положительном направлении): (отсчитываемый в положительном направлении):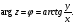 Аргумент может принимать любые значения, но при заданном модуле углы, отличающиеся на 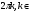 Z , соответствуют одному и тому же числу Z , соответствуют одному и тому же числу  . .Для числа 0 аргумент не определен. Действительная и мнимая части комплексного числа связаны с модулем и аргументом очевидными соотношениями: 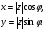 Тогда 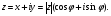 Это и есть тригонометрическая форма записи комплексного числа  . .Заметим, что операции сложения и вычитания выглядят в алгебраической форме просто и естественно, но формулы для умножения и деления кажутся весьма громоздкими. Если же мы перейдем к тригонометрической форме записи комплексного числа, то получим: 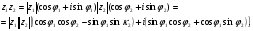 Итак, модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов сомножителей. Несложно показать, что при делении модули делятся, а аргументы вычитаются: так как 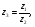 то то 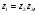 поэтому поэтому 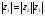 и и 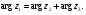 Значит, Значит, 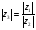 и и 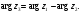 3. Возведение комплексного числа в степень и извлечение корня. Из формулы для умножения комплексных чисел в тригонометрической форме сразу же следует формула для возведения комплексного числа в степень – формула Муавра: 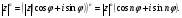 Теперь попробуем извлечь из комплексного числа корень произвольной степени. В отличие от действительных чисел это всегда возможно. Пусть дано комплексное число 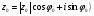 . Мы должны найти такое комплексное число . Мы должны найти такое комплексное число  ,что ,что 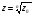 , т.е. , т.е. 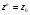 . Это означает, что . Это означает, что 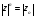 и и 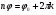 . Отсюда . Отсюда 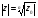 и и 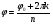 . Если при одном и том же модуле аргументы отличаются на . Если при одном и том же модуле аргументы отличаются на 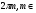 Z, то они определяют одно и то же комплексное число. Значит, различные корни мы получим, когда Z, то они определяют одно и то же комплексное число. Значит, различные корни мы получим, когда 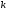 пробегает числа 0,1,… пробегает числа 0,1,…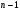 . Остальные значения новых корней не дадут. . Остальные значения новых корней не дадут.Геометрически это выглядит так: корни 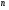 -й степени из комплексного числа -й степени из комплексного числа  находятся на окружности с центром в начале координат радиуса находятся на окружности с центром в начале координат радиуса 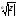 в вершинах правильного в вершинах правильного 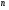 -угольника. -угольника.4. Важное замечание. Мы расширили систему действительных чисел с целью иметь возможность решить уравнение 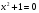 и, как следствие, все квадратные уравнения. Как мы видим, в построенной системе комплексных чисел можно еще и извлекать корни любой степени, т.е.решать алгебраические уравнения вида и, как следствие, все квадратные уравнения. Как мы видим, в построенной системе комплексных чисел можно еще и извлекать корни любой степени, т.е.решать алгебраические уравнения вида 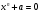 . Оказывается, произвольный многочлен с комплексными коэффициентами имеет комплексный корень, более того, он имеет ровно . Оказывается, произвольный многочлен с комплексными коэффициентами имеет комплексный корень, более того, он имеет ровно 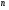 комплексных корней с учетом их кратностей. Это утверждение называется основной теоремой алгебры, но доказательство этой теоремы выходит за рамки нашего курса. комплексных корней с учетом их кратностей. Это утверждение называется основной теоремой алгебры, но доказательство этой теоремы выходит за рамки нашего курса. |
