Курсовая. курсовая работа. Поверхности второго порядка
 Скачать 231.87 Kb. Скачать 231.87 Kb.
|
|
КУРСОВАЯ РАБОТА на тему «Поверхности второго порядка» Содержание Введение Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени. В данной работе мы подробно изучим эту тему. Целью данной курсовой работы являются формы поверхности второго порядка. Закрепление полученных теоретических знаний и практических навыков по изучению и анализу поверхностей второго порядка. Задачами курсовой работы является: Изучить классификацию поверхностей второго порядка; Изучить классификацию нецентральных поверхностей второго порядка Исследовать форму поверхности методом сечений плоскостями, построить линии, полученные в сечениях; Построить поверхность в канонической системе координат. Глава 1. Теоретическая часть1.1 Общие понятия Поверхностью второго порядка S называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида: 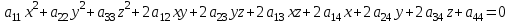 , (1) , (1)где по крайней мере один из коэффициентов 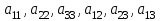 отличен от нуля. отличен от нуля.Уравнение (1) называют общим уравнением поверхности второго порядка S, а систему координат Oxyz называют общей системой координат. Теорема: Для произвольной поверхности S, заданной общим уравнением существует такая декартова прямоугольная система координат 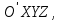 что в этой системе поверхность S имеет уравнение одного из следующих семнадцати канонических видов. что в этой системе поверхность S имеет уравнение одного из следующих семнадцати канонических видов.1) 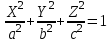 — эллипсоид, — эллипсоид,2) 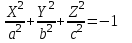 — мнимый эллипсоид, — мнимый эллипсоид,3) 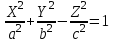 — однополостный гиперболоид, — однополостный гиперболоид,4) 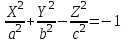 — двуполостный гиперболоид, — двуполостный гиперболоид,5) 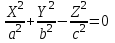 — конус, — конус, 6) 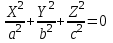 — мнимый конус (точка), — мнимый конус (точка), 7) 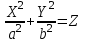 — эллиптический параболоид, — эллиптический параболоид,8) 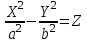 — гиперболический параболоид, — гиперболический параболоид,9)  — эллиптический цилиндр, — эллиптический цилиндр,10) 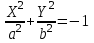 — мнимый эллиптический цилиндр, — мнимый эллиптический цилиндр,11) 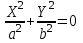 — две мнимые пересекающиеся плоскости (ось — две мнимые пересекающиеся плоскости (ось O'Z), 12) 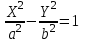 — гиперболический цилиндр, — гиперболический цилиндр,13) 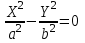 — две пересекающиеся плоскости, — две пересекающиеся плоскости,14)  — параболический цилиндр, — параболический цилиндр,15) 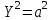 — две параллельные плоскости, — две параллельные плоскости,16) 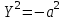 — две мнимые параллельные плоскости, — две мнимые параллельные плоскости,17)  — две совпадающие плоскости (плоскость XOZ). — две совпадающие плоскости (плоскость XOZ).В вышеперечисленных уравнениях a, b, c, p — положительные параметры. Систему координат 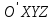 называют канонической. называют канонической.1.2 Классификация поверхностей второго порядка 1. Классификация центральных поверхностей. Пусть S — центральная поверхность второго порядка. Перенесем начало координат в центр этой поверхности, а затем произведем стандартное упрощение уравнения этой поверхности. В результате указанных операций уравнение поверхности примет вид a11х2 + а22у2 + a33z2 + а44 = 0 (2) Так как инвариант I3 для центральной поверхности отличен от ноля и его значение, вычисленное для уравнения (2) , равно a11 • а22 • a33 , то коэффициенты a11 ,а22 , a33 удовлетворяют условию: Возможны следующие случаи: 1. Коэффициенты a11 ,а22 , a33 одного знака, а коэффициент а44 отличен от нуля. В этом случае поверхность S называется эллипсоидом. Если коэффициенты a11 ,а22 , a33 , а44 одного знака, то левая часть (2) ни при каких значениях х, у, z не обращается в нуль, т. е. уравнению поверхности S не удовлетворяют координаты никакой точки. В этом случае поверхность S называется мнимым эллипсоидом. Если знак коэффициентов a11 ,а22 , a33 противоположен знаку коэффициента а44 , то поверхность S называется вещественным эллипсоидом. В дальнейшем термином «эллипсоид» мы будем называть лишь вещественный эллипсоид. Обычно уравнение эллипсоида записывают в канонической форме. Очевидно, числа 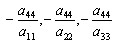 положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение эллипсоида (2) можно записать в следующей форме: 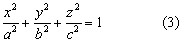 Уравнение (3) называется каноническим уравнением эллипсоида. Если эллипсоид задан своим каноническим уравнением (3), то оси Ох, Оу и Оz. называются его главными осями. 2. Из четырех коэффициентов a11 ,а22 , a33 , а44 два одного знака, а два других—противоположного. В этом случае поверхность S называется однополостным гиперболоидом. Обычно уравнение однополостного гиперболоида записывают в канонической форме. Пусть, ради определенности, a11 > 0, а22 > 0, a33 < 0, а44 < 0. Тогда числа 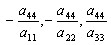 положительны. Обозначим эти числа соответственно а2, b2, с2. После несложных преобразований уравнение (2) однополостного гиперболоида можно записать в следующей форме:  Уравнение (4) называется каноническим уравнением однополостного гиперболоида. Если однополостный гиперболоид задан своим каноническим уравнением (4), то оси Ох, Оу и Oz называются его главными осями. 3. Знак одного из первых трех коэффициентов a11 ,а22 , a33 , а44 противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двуполостным гиперболоидом. Запишем уравнение двуполостного гиперболоида в канонической форме. Пусть, ради определенности, a11 < 0, а22 < 0, a33 > 0, а44 < 0. Тогда: 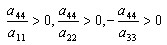 Обозначим эти числа соответственно через a2, b2, с2. Поcли несложных преобразований уравнение (2) двуполостного гиперболоида можно записать в следующей форме:  Уравнение (5) называется каноническим уравнением двуполостного гиперболоида. Если двуполостный гиперболоид задан своим каноническим уравнением, то оси Ох, Оу и Оz называются его главными осями. 4. Коэффициент а44 равен нулю. В этом случае поверхность S называется конусом второго порядка. Если коэффициенты a11 , а22 , a33 одного знака, то левая часть (2) обращается в нуль (а44 = 0) лишь для х=у=z=0, т. е. уравнению поверхности S удовлетворяют координаты только едной точки. В этом случае поверхность S называется мнимым конусом второго порядка. Если коэффициенты a11 , а22 , a33 имеют разные знаки, то поверхность S является вещественным конусом второго порядка. Обычно уравнение вещественного конуса второго порядка записывают в канонической форме. Пусть, ради определенности, a11 > o, а22 > 0, a33 < 0. Обозначим 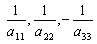 соответственно через а2, b2, с2. Тогда уравнение (2) можно записать в виде 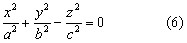 Уравнение (6) называется каноническим уравнением вещественного конуса второго порядка. 1.3 Классификация нецентральных поверхностей второго порядка Пусть S — нецентральная поверхность второго порядка, т. е. поверхность, для которой инвариант I3 равен нулю. Произведем стандартное упрощение уравнения этой поверхности. В результате уравнение поверхности примет вид a´11х´2 + а´22у´2 + a´33z´2 + 2а´14 x´ + 2а´24у´+2а´34z´ +а´44 = 0 (7) для системы координат Ox´y´z´ Так как инвариант I3 = 0 и его значение, вычисленное для уравнения (7) , равно a´11 • а´22 • a´33 , то один или два из коэффициентов a´11 , а´22 , a´33 равны нулю. В соответствии с этим рассмотрим следующие возможные случаи. 1. Один из коэффициентов a´11 , а´22 , a´33 равен нулю. Ради определенности будем считать, что a´33 = 0 (если равен нулю какой-либо другой из указанных коэффициентов, то можно перейти к рассматриваемому случаю путем переименования осей координат). Перейдем от координат х', у', z' к новым координатам х, у, z по формулам Подставляя х', у' и z', найденные из (8), в левую часть (7) и заменяя затем a´11 на a11 , а´22 на а22 , а´34 на p и а´44 на q , получим следующее уравнение поверхности S в новой системе координат Oxyz : a11х2 + а22у2 + 2pz + q = 0 (9) 1) Пусть р = 0, q = 0. Поверхность S распадается на пару плоскостей При этом, очевидно, эти плоскости будут мнимыми, если знаки a11 и а22 одинаковы, и вещественными, если знаки a11 и а22 различны. 2) Пусть р = 0, q ≠ 0. Уравнение (9) принимает вид a11х2 + а22у2 + q = 0 (10) Известно, что уравнение (10) является уравнением цилиндра с образующими, параллельными оси Оz. При этом если a11 , а22 , q имеют одинаковый знак, то левая часть (10) отлична от нуля для любых х и y, т. е. цилиндр будет мнимым. Если же среди коэффициентов a11 , а22 , q имеются коэффициенты разных знаков, то цилиндр будет вещественным. Отметим, что в случае, когда a11 и а22 имеют одинаковые знаки, a q — противоположный, то величины положительны. 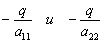 Обозначая их соответственно через а2 и b2, мы приведем уравнение (10) к виду 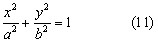 Таким образом, в отмеченном случае мы имеем эллиптический цилиндр. В случае, a11 и а22 имеют различные знаки, мы получим гиперболический цилиндр. Легко убедиться, что уравнение гиперболического цилиндра может быть приведено к виду 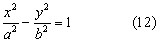 3) Пусть р≠0. Произведем параллельный перенос системы координат, выбирая новое начало в точке с координатами 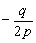 (0, 0,). При этом оставим старые обозначения координат х, у, z. Очевидно, для того чтобы получить уравнение поверхности S в новой системе координат, достаточно заменить в уравнении (9) Получим следующее уравнение: a11х2 + а22у2 + 2pz = 0 (13) Уравнение (13) определяет так называемые параболоиды. Причем если a11 и а22 имеют одинаковый знак, то параболоид называется эллиптическим. Обычно уравнение эллиптического параболоида записывают в канонической форме:  Уравнение (14) легко получается из (13). Если a11 и а22 имеют разные знаки, то параболоид называется гиперболическим. Каноническое уравнение гиперболического параболоида имеет вид  Это уравнение также легко может быть получено из (13). 2°. Два из коэффициентов a´11 , а´22 , a´33 равны нулю. Ради определенности будем считать, что a´11 = 0 и а´22 = 0 Перейдем от х,', у', z' к. новым координатам х, у, z по формулам : 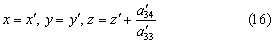 Подставляя х', у' и z' , найденные из (16) в левую часть (7) и заменяя затем a´33 на a33 , a´14 на р , a´24 на q и a´44 на r , получим следующее уравнение поверхности S в новой системе координат Охуz : a33 z2 + 2px + 2qy + r = 0 (17)  1) Пусть р=0, q=0. Поверхность S распадается на пару параллельных плоскостей При этом, очевидно, эти плоскости будут мнимыми, если знаки a33 и r одинаковы, и вещественными, если знаки a33 и r различны, причем при r = 0 эти плоскости сливаются в одну. 2) Хотя бы один из коэффициентов р или q отличен от нуля. В этом случае повернем систему координат вокруг оси Oz так, чтобы новая ось абсцисс стала параллельной плоскости 2рх+2qy+r=0. Легко убедиться, что при таком выборе системы координат, при условии сохранения обозначения х, у и z для новых координат точек, уравнение (17) примет вид a33 z2 + 2q´y = 0 (19) которое является уравнением параболического цилиндра с образующими, параллельными новой оси Ох. 1.4 Исследование формы поверхности второго порядка методом сечения плоскостями Если дано каноническое уравнение поверхности S, то представление о поверхности можно получить по форме линий пересечения ее плоскостями: Z = h— параллельными координатной плоскости XO'Y, X = h — параллельными координатной плоскости YO'Z, Y = h — параллельными координатной плоскости XO'Z. Практическая частьРешение задач Дано: 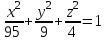 ; ;Это эллипсоид в прямоугольной декартовой системе координат Oxyz, где оси OX, OY, OZ — оси симметрии. Рассмотрим линии 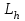 плоскостями =h (h=const): плоскостями =h (h=const):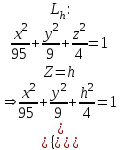 (1) (1)Плоскость Z=h параллельна плоскости Oxy. Уравнения проекций 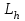 на Oxy имеют вид: на Oxy имеют вид: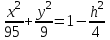 Если 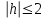 , то , то  , и тогда поделим обе части уравнения на , и тогда поделим обе части уравнения на 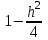 , получим: , получим: 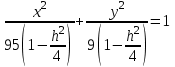 Это уравнение эллипсов с полуосями 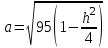 , ,  ; увеличивающиеся с уменьшением ; увеличивающиеся с уменьшением 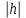 , центр эллипса (0;0;h) , центр эллипса (0;0;h)При различных h имеем: 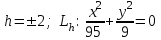 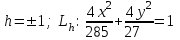 Если 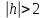 , тогда , тогда 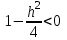 и значит линии и значит линии 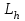 удовлетворяющих уравнению(1) нет. удовлетворяющих уравнению(1) нет.Рассмотрим 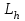 полученные в сечениях эллипсоида плоскостями X=h: полученные в сечениях эллипсоида плоскостями X=h: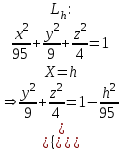 (2) (2)Уравнение проекций 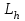 на YOZ. на YOZ.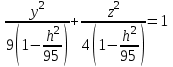 Это уравнение эллипсов с полуосями 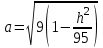 , , 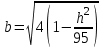 ; ; Если  , то a=3, b=2, и , то a=3, b=2, и 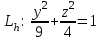 Если 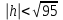 , тогда мы получаем семейство эллипсов: , тогда мы получаем семейство эллипсов: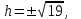 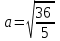 , , 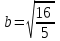 ; ; 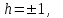  , , 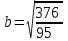 ; ;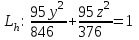 Если  , тогда , тогда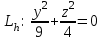 — это уравнение точки с координатами (h;0;0). — это уравнение точки с координатами (h;0;0).Если 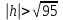 , тогда , тогда  и значит линии и значит линии 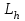 удовлетворяющих уравнению (2) нет. удовлетворяющих уравнению (2) нет.3. Рассмотрим 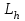 полученные в сечениях эллипсоида плоскостями Y=h: полученные в сечениях эллипсоида плоскостями Y=h: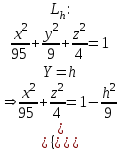 (3) (3)Уравнения эллипсов, проекций 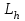 на YOZ и имеют центры (0;h;0). на YOZ и имеют центры (0;h;0).Полуоси  , , 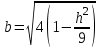 Если 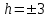 , тогда , тогда 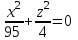 , уравнение точек с координатами (0;h;0). , уравнение точек с координатами (0;h;0).Если 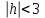 , тогда мы получаем семейство эллипсов: , тогда мы получаем семейство эллипсов: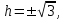 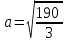 , ,  ; ; 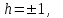  , ,  ; ;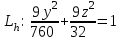 Если 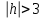 , тогда , тогда  и значит линии и значит линии 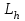 удовлетворяющих уравнению (3) нет. удовлетворяющих уравнению (3) нет.Построим однополостный гиперболоид  в канонической системе координат 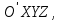 проанализировав уравнение поверхности и результаты исследования методом сечения ее плоскостями. проанализировав уравнение поверхности и результаты исследования методом сечения ее плоскостями.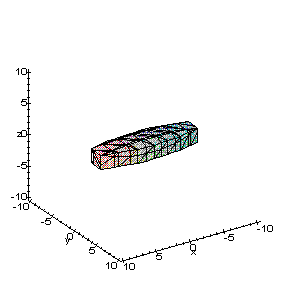 ВыводПроанализировав уравнение эллипсоида 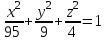 , получили некоторые представления о форме эллипсоида. , получили некоторые представления о форме эллипсоида.Из уравнения следует, что оси OX, OY, OZ — оси симметрии, плоскости XOY, YOZ, XOZ — плоскости симметрии. Рассекая поверхность плоскостями y=h,z=h,x=h, в сечениях имеем эллипсы, наибольшие из которых получаются в плоскостях x=0, y=0, z=0, полуоси их уменьшаются с увеличением 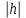 , вершины эллипсов имеют координаты , вершины эллипсов имеют координаты 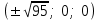 по оси X; по оси X; 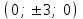 по оси Y; по оси Y; 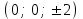 по оси Z. по оси Z. Список используемой литературыВ.А. Ильин, Э.Г. Позняк «Аналитическая геометрия» Копылова Т. В. Конспект лекций по линейной алгебре; Копылова Т. В. Линейная алгебра. — Дубна: Международный университет природы, общества и человека «Дубна», 1996; Ефимова Л. В., Демидович Б. П. Линейная алгебра и основы математического анализа. — М: Наука, 1993. |
