Анализ задач_Ляшенко_Г.Г._4_семестр. Анализ задач на построение сечений многогранников плоскостями
 Скачать 244.36 Kb. Скачать 244.36 Kb.
|
|
Анализ задач на построение сечений многогранников плоскостями Ляшенко Г.Г. Для анализа задач на построение сечений многогранников плоскостями были взяты учебники для 10 – 11 классов: 1) Геометрия. 10 – 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни/Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 22-е изд. – М.: Просвещение, 2013. – 255 с.; 2) Александров А.Д. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10 – 11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни / А.Д. Александров, А.Л. Вернер, В.И. Рыжик. – М.: Просвещение, 2014. – 255 с.; и материалы с сайта https://math-ege.sdamgia.ru. Рассмотрим первый учебник. В учебнике приводятся примеры задач на построение сечений тетраэдра и параллелепипеда. Первый пример: На ребрах АВ, BD и CD тетраэдра ABCD отмечены точки M, N и P^ 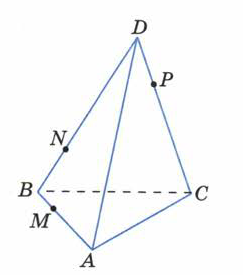 Построить сечение тетраэдра плоскостью MNP. Сечение в данном случае строится методом следов: 1) Чтобы построить сечение, необходимо построить прямую, по которой пересекаются плоскости MNP и АВС. Одна точка этой прямой уже есть – это точка М. вторую точку можно найти как точку пересечения прямой NP и прямой ВС. Т.к. NP и ВС лежат в одной плоскости, продолжим их до их пересечения. Получим точку Q: 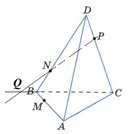 2) Точки Q и М лежат в плоскости АВС. Соединим их. Так как точки Q и М принадлежат и плоскости АВС, и плоскости MNP, то прямая QM – прямая, по которой пересекаются эти плоскости: 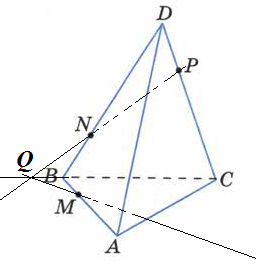 Прямая QM лежит с ребром АС в одной плоскости АВС и пересекает его в точке S. Так как P и S принадлежат и плоскости ADC, и плоскости MNP, то прямая SP является прямой пересечения этих плоскостей. MNPS – искомое сечение: 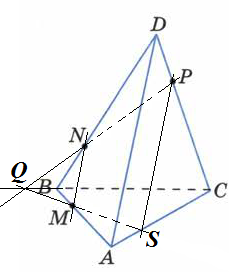 В учебнике также рассматривается случай, если прямые NP и ВС параллельны. В этом случае прямая NP параллельна АВС. Тогда плоскость MNP пересекает плоскость АВС по прямой MQ, параллельной прямой NP: 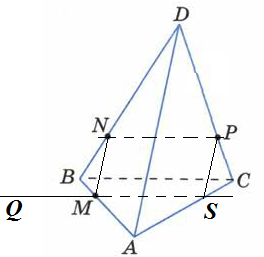 Еще один пример построения сечения по точкам приведен пример построения сечения параллелепипеда: На ребрах параллелепипеда даны три точки А, В и С. Построить сечение параллелепипеда плоскостью АВС. Здесь также возможны разные случаи. 1) Все три точки находятся на ребрах, выходящих из одной вершины. В этом случае все точки можно соединить, так как А и В находятся в одной плоскости, А и С – в другой, В и С – в третьей. 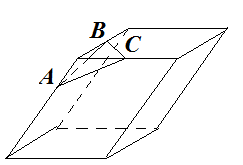 2) Второй случай - точки расположены на параллельных ребрах. Тогда сначала соединяют точки А и В, В и С. Так как противоположные стороны параллелепипеда параллельны друг другу, то можно применить свойство плоскости, пересекающей параллельные плоскости – она пересекает их по параллельным прямым. Следовательно, проводим через точку А прямую, параллельную прямой ВС, а через точку С параллельно прямой АВ. Проведенные прямые в плоскости нижнего основания дают точки пересечения E и D. Пятиугольник ABCDE – искомое сечение: 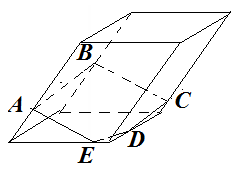 То же сечение можно построить и методом следов: 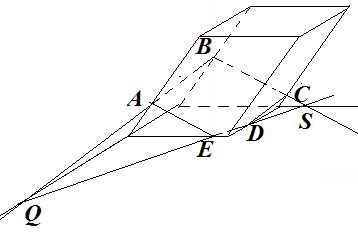 3) Третий случай: две точки лежат на ребрах, исходящих из одной вершины, а третья – на ребре, пересекающемся с одним из данных: 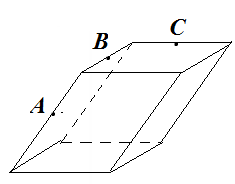 В этом случае сначала строят прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания. Для этого проводят прямую АВ до пересечения с продолжением нижнего ребра в точке М. Затем через точку М проводят прямую в плоскости нижнего основания параллельно прямой ВС. Это прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с ребрами нижнего основания в точках E и F. Через точку Е проводят прямую, параллельную прямой АВ, получим точку D. Затем проводят отрезки AF и CD, шестиугольник ABCDEF – искомое сечение: 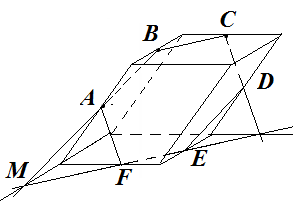 Третий пример – построение сечения пирамиды параллельно основанию: Точка М лежит на боковой грани ADB тетраэдра DABC. Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию АВС. Так как плоскость сечения параллельна плоскости АВС, то она параллельна прямым АВ, ВС и СА. Тогда плоскость сечения пересекает боковые грани тетраэдра по прямым, параллельным сторонам грани АВС. Тогда проводим через точку М прямую, параллельную АВ, получим точки пересечения прямой с боковыми ребрами AD и DB – P и Q. Через точку Р проведем параллельную АС, на пересечении прямой с ребром DC получим точку R. Треугольник PQR – искомое сечение: 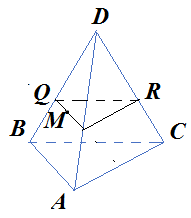 В учебнике предлагается несколько упражнений на построение сечения с разными условиями: для построения сечения параллелепипеда - через три точки в разных положениях – в вершинах параллелепипеда, на гранях, на ребрах параллелепипеда; для построения сечения тетраэдра также через три точки или через ребро и точку. Кроме того, в учебнике представлены задачи на построение сечения плоскостью, проходящей через заданную точку или прямую, параллельно прямой (обычно ребру или диагонали грани) или плоскости. Проиллюстрируем некоторые из предлагаемых задач без подробного решения: № 73. Сечение тетраэдра плоскостью, проходящей через три заданные точки: 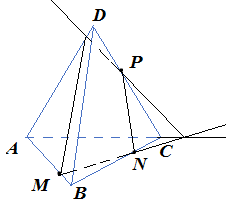 № 75. Сечение тетраэдра через заданную прямую (ребро) и точку: 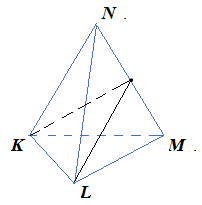 № 79. Сечение параллелепипеда плоскостью, проходящей через три вершины: 1) случай – через точки АВС1: 2) случай – через точки АСС1: 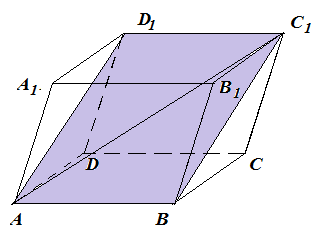 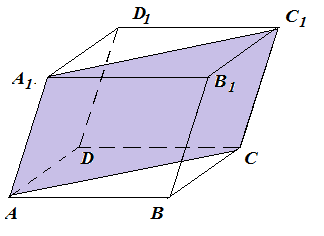 № 82. Сечение параллелепипеда плоскостью, проходящей через точку грани, параллельно: 1) грани ABCD: 2) плоскости BDD1: 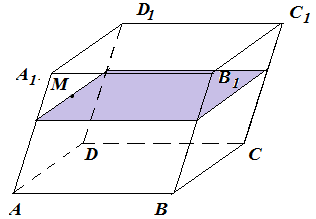 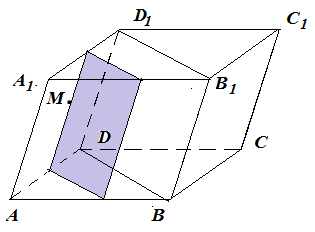 № 86. Сечение параллелепипеда плоскостью, проходящей через диагональ АС, параллельно BD1: 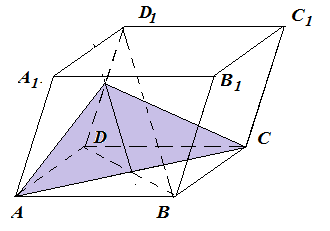 № 233. Сечение призмы плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости: 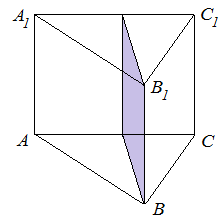 № 244. Сечение призмы плоскостью, проходящей через заданную точку перпендикулярно заданной прямой: 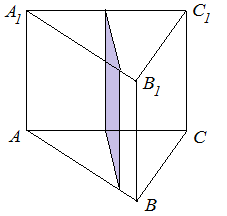 Рассмотрим задачи на построение сечения многогранников, представленные в учебнике по геометрии для 10 – 11 классов Александрова А.Д. В изложении теоретического материала нет примеров решения подобных задач. Но среди упражнений имеется ряд задач на построение сечений многогранников. Например, задача на вычисление площади сечения плоскостью, проходящей через заданную точку параллельно основанию пирамиды, через заданную прямую параллельно боковому ребру пирамиды, через заданную прямую перпендикулярно боковому ребру пирамиды, через заданную точку перпендикулярно боковой грани пирамиды, а также через заданную прямую, проходящую под заданным углом к основанию пирамиды. Среди материалов для подготовки к ЕГЭ по математике – материалы, опубликованные на сайте «Решу ЕГЭ». Среди представленных задач – задачи на построение сечений параллелепипеда, пирамиды, призмы. Построение сечения входит в задачу как необходимая часть решения. Анализ учебных материалов показывает, что учащимся предлагается освоить решение задач на построение сечения многогранников в следующих случаях: - построение сечения многогранника плоскостью, проходящей через заданные точки непосредственным соединением; - построение сечения многогранника плоскостью, проходящей через заданную прямую и точку соединением известных элементов; - построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости; - построение сечения многогранника плоскостью, проходящей через заданную прямую параллельно другой заданной прямой; - построение сечения многогранника плоскостью, проходящей через заданную точку параллельно двум заданным пересекающимся прямым; - построение сечения многогранника плоскостью, проходящей через заданную точку параллельно двум заданным скрещивающимся прямым; - построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости; - построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой. |
