Prikladnaia_matematika 31 мая. Основные понятия комплексных чисел Определение комплексного числа в алгебраической форме, действия над ними
 Скачать 69.43 Kb.
|
|
Основные понятия комплексных чисел Определение комплексного числа в алгебраической форме, действия над ними. Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i 2 = -1. Исходя из этого, получим следующее определение комплексного числа. Комплексным числом называется выражение вида a + bi, где a и b - действительные числа. При этом выполняются условия: а) Два комплексных числа a1 + b1i и a2 + b2i равны тогда и только тогда, когда a1=a2, b1=b2. б) Сложение комплексных чисел определяется правилом: (a1 + b1i) + (a2 + b2i) = (a1 + a2) + (b1 + b2) i. в) Умножение комплексных чисел определяется правилом: (a1 + b1i) (a2 + b2i) = (a1a2 - b1b2) + (a1b2 - a2b1) i. Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число. Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0 Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a. Комплексное число a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi. Два комплексных числа z = a + bi и  = a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.Над комплексными числами в алгебраической форме можно выполнять следующие действия. 1) Сложение. Суммой комплексных чисел z1 = a1 + b1 i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть - сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2) i. Числа z1 и z2 называются слагаемыми. Сложение комплексных чисел обладает следующими свойствами: 1º. Коммутативность: z1 + z2 = z2 + z1. 2º. Ассоциативность: (z1 + z2) + z3 = z1 + (z2 + z3). 3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0 2) Вычитание. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 =z1. Разность комплексных чисел существует и притом единственная. 3) Умножение. Произведением комплексных чисел z1=a1+ b1 i и z2=a2+b2i называется комплексное число z, определяемое равенством: z = (a1 a2 – b1b2) + (a1b2 + a2b1) i. Числа z1 и z2 называются сомножителями. Умножение комплексных чисел обладает следующими свойствами: 1º. Коммутативность: z1z2 = z2 z1. 2º. Ассоциативность: (z1z2)z3 = z1 (z2z3) 3º. Дистрибутивность умножения относительно сложения: (z1 + z2) z3 = z1z3 + z2z3. 4º. z ·  = (a + bi) (a – bi) = a2 + b2 - действительное число.На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части. 4) Деление. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i. 5) а) Возведение в целую положительную степень. Чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления. б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей. С помощью комплексных чисел можно решать квадратные уравнения, у которых отрицательный дискриминант. Геометрическое изображение комплексных чисел. Модуль и аргументы комплексного числа. Любое комплексное число (кроме нуля) z=a+bi можно записать в тригонометрической форме: z=|z|∙(cosφ+isinφ), где |z| – это модуль комплексного числа, а φ – аргумент комплексного числа. Изобразим на комплексной плоскости число z=a+bi . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что a>0, b>0 : 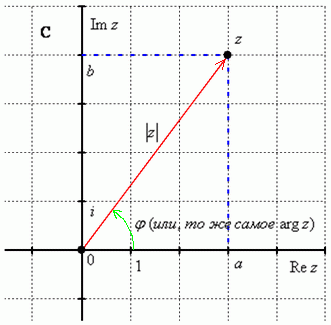 Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом. Модуль комплексного числа z стандартно обозначают: |z| или r. По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:  . Данная формула справедлива для любых значений a и b. Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0. Аргумент комплексного числа z стандартно обозначают: φ или arg z. Из геометрических соображений получается следующая формула для нахождения аргумента:  Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Формулы для нахождения  в зависимости от а и b:1.  2.  3.  4.  5.  6.  7.  8.  Решение алгебраических уравнений. Алгебраическое уравнение — уравнение вида: P(x1, x2, …, xn)=0, где P — многочлен от переменных x1,x2,…,xn, которые называются неизвестными. Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x1, x2, …, xn)=0 называется алгебраическим уравнение над полем F. Степенью алгебраического уравнения называют степень многочлена P. Связанные определения. Значения переменных x1, x2, …, xn, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения. Уравнения, сводящиеся к алгебраическим. Биквадратными называются уравнения вида: ах4 + bх2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0. Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х2. Новое квадратное уравнение относительно переменной у: ay2+by+c=0. Решая это уравнение, мы получаем корни квадратного уравнения y1 и y2. Решая эти два уравнения (y1=x12 и y2=x12) относительно переменной x, мы получаем корни данного биквадратного уравнения. Порядок действий при решении биквадратных уравнений Ввести новую переменную у=х2 Подставить данную переменную в исходное уравнение Решить квадратное уравнение относительно новой переменной После нахождения корней (y1; y2) подставить их в нашу переменную у=х2 и найти исходные корни биквадратного уравнения 2. Симметрические уравнения. Симметрическим уравнением 3-ей степени называют уравнение вида ax3 + bx2 + bx + a = 0, где a, b – заданные числа. Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений: 10. У любого симметрического уравнения нечетной степени всегда есть корень, равный -1. 20. У симметрического уравнения корней, равных нулю, нет. 30. При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом. 3. Возвратные уравнения. Уравнение вида: anxn+an-1xn-1+…+a1x+a0=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. an-1=ak, при k=0, 1, …, n. Порядок действий при решении возвратных уравнений вида ax4 + bx3 + cx2 + bx + a = 0: разделить левую и правую части уравнения на  . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;группировкой привести полученное уравнение к виду  ввести новую переменную  , тогда выполнено , то есть  ; в новых переменных рассматриваемое уравнение является квадратным: at2 +bt+c–2a=0; решить его относительно t, возвратиться к исходной переменной. Элементы линейной алгебры Матрицы и действия над ними. Экономико-математические методы. Матричные модели. Определитель матрицы. Системы линейных алгебраических уравнений и методы их решения (метод обратной матрицы, метод Гаусса, метод Крамера). Моделирование и решение задач линейного программирования. Введение в анализ Функции двух и нескольких переменных, способы задания, символика, область определения. Предел функции. Бесконечно малые функции. Метод эквивалентных бесконечно малых величин. Раскрытие неопределённости вида 0/0 и ∞/∞. Замечательные пределы. Непрерывность функции. Дифференциальное исчисление Производная функции. Первый дифференциал функции, связь с приращением функции. Основные правила дифференцирования. Производные и дифференциалы высших порядков. Возрастание и убывание функций. Экстремумы функций. Частные производные функции нескольких переменных. Полный дифференциал. Частные производные высших порядков. Интегральное исчисление и дифференциальные уравнения Первообразная функция и неопределённый интеграл. Основные правила неопределённого интегрирования. Задача нахождения площади криволинейной трапеции. Определённый интеграл. Формула Ньютона-Лейбница. Основные свойства определённого интеграла. Интегрирование по бесконечному промежутку. Интегрирование неограниченных функций. Примеры задач, приводящих к дифференциальным уравнениям. Основные понятия и определения дифференциальных уравнений. Теория вероятностей и математическая статистика Элементы комбинаторики: перестановки, размещения, сочетания. Генерирование основных комбинаторных объектов. Основные понятия теории вероятностей. Классическое, геометрическое и статистическое определение вероятности. Теорема сложения и умножения вероятностей. Формула полной вероятности. Формула Байеса. Бином Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля. Генеральная и выборочная совокупности. Вариационный ряд и его графическое изображение. Числовые характеристики вариационных рядов. Правило суммы и правило произведения. Сочетания, размещения и перестановки с повторениями и без повторений. |
