Ответ Оп Матрицей a размерности Sxn называется прямоугольная таблица из чисел, состоящая из s строк и n столбцов
 Скачать 7.71 Mb. Скачать 7.71 Mb.
|
|
Напомним, что упорядоченный набор векторов образует базис, если: 1) эти векторы линейно независимы, 2) любой вектор в пространстве линейно выражается через них. Теорема 4. Любая упорядоченная тройка некомпланарных векторов образует базис в пространстве. Доказательство теоремы очевидно: любые три некомпланарных вектора линейно независимы и любой вектор является их линейной комбинацией. Справедлива также Теорема 4а. Любые два неколлинеарных вектора, лежащие в плоскости, образуют базис в этой плоскости. Напомним, что равенство 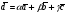 называют разложением вектора 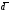 по базису по базису 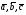 , а числа , а числа 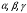 - координатами вектора - координатами вектора 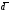 в базисе в базисе 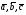 . Эти координаты определены однозначно. . Эти координаты определены однозначно. Зафиксировав базис 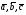 в пространстве свободных векторов и точку в пространстве свободных векторов и точку 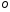 в пространстве – ее называют началом координат, - мы можем определить так называемые аффинные координаты произвольной точки в пространстве – ее называют началом координат, - мы можем определить так называемые аффинные координаты произвольной точки  нашего пространства. нашего пространства.Упорядоченная тройка некомпланарных векторов е1, e2,e3 назвается базисом в множестве всех геометрических векторов. Всякий геометрический вектор а может быть представлен единственным образом в виде: А = x1e1+x2e2+x2e3. Числа x1,x2,x3 называются координатами вектора а в базисе (e1,e2,e3) 34. Понятие проекции вектора на ось. Свойства проекций!  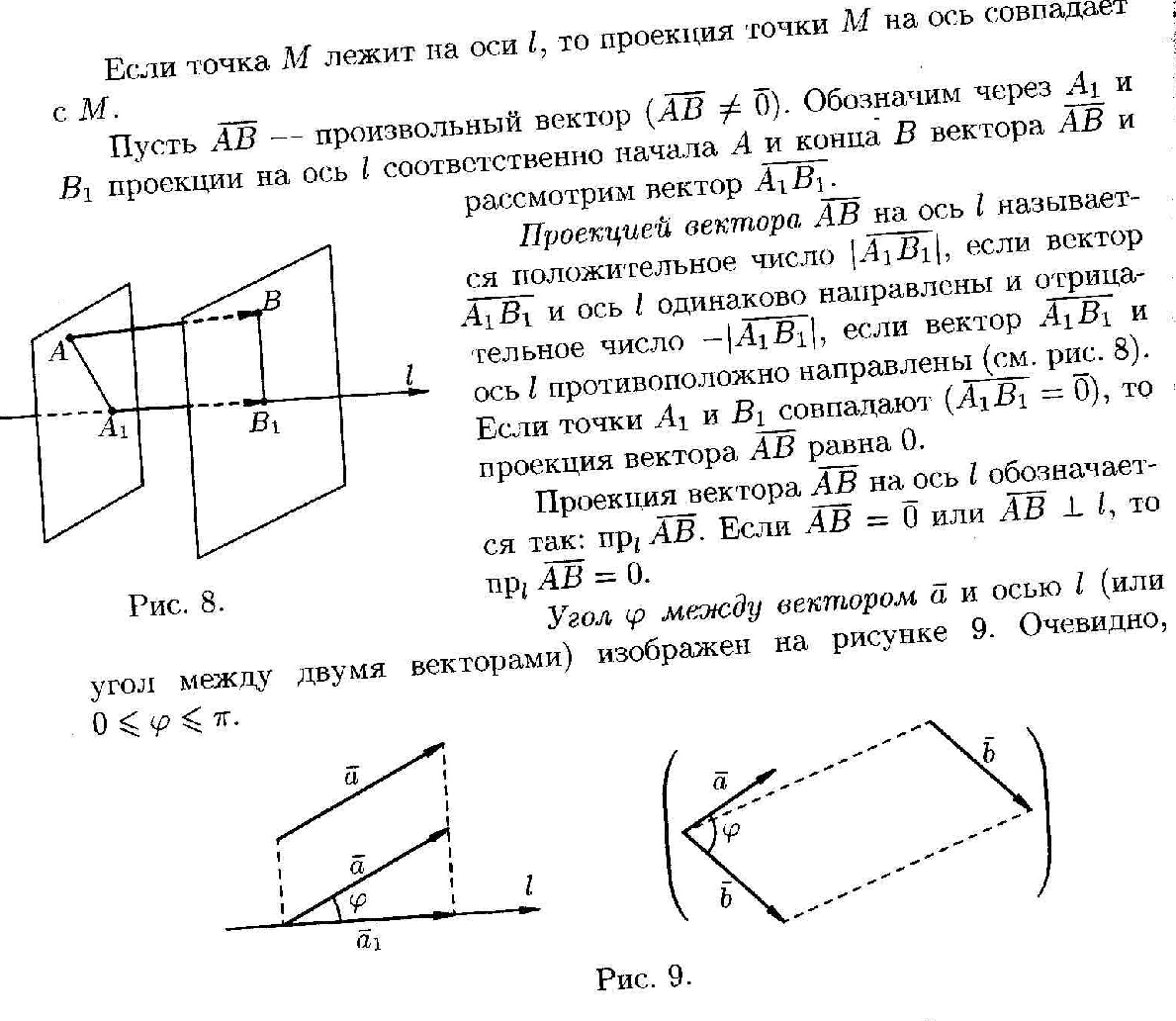  Свойство 2: Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось. Свойство 3: При умножение вектора а на число b его проекция умножается на это число Проекция а = а*cosф. Сosф = (а^e) – угол между а и е(один из базис векторов) 35.Прямоугольная система координат. Нахождение координат вектора по координатам его начала и конца Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Иначе говоря, положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. рис. 2). 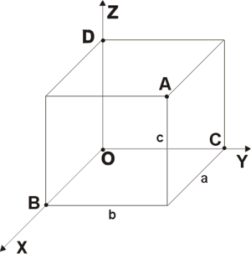 Рис. 2 Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так:  33.Геометрические векторы их координаты, линейные операции над ними и их свойствОсновные понятия. Геометрическим вектором (или просто вектором) будем называть направленный отрезок. Обозначать его будем 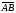 , где , где 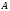 - начало вектора, - начало вектора, 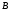 - конец вектора, или одной буквой - конец вектора, или одной буквой 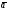 . Начало вектора называют еще точкой приложения вектора. Длину вектора будем обозначать, используя знак модуля: . Начало вектора называют еще точкой приложения вектора. Длину вектора будем обозначать, используя знак модуля: 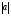 или или 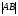 . . Вектор называется нулевым, если его начало и конец совпадают. Определение. Векторы называются коллинеарными, если они лежат на параллельных прямых. Определение. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление. Все нулевые векторы считаются равными.   36. Скалярное произведение векторов и его свойства Определние: Величина (a,b)=|a|*|b|*cos(a^b) называется скалярным пр-ем векторов a и b. Очевидно, что можно записать (a,b)=|a|*(проекция b на а) и наоборот. Свойства скалярного произведения: 1) (a,b)=(a,b); 2) (a,b+c)= (a,b)+(a,c); 3)(w*a,b)=w*(a,b)=(a,w*b),w=const; 4)(a,a)≥0, причем (a,a)=0, когда a=0. Доказательство 2го: (a,b+c)=|a|*(проекция (b+c) на a)= |a|*(проекция b на а)+|a|*(проекция c на а)= (a,b)+(a,c).Скалярное произведение равно 0 тогда и только тогда, когда a перпендикулярно b, или a=0, или b=0. 9.1. Скалярное произведение. Прежде всего, определим, что такое угол между двумя произвольными векторами 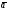 и и 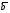 . Возьмем любую точку и приложим к ней оба вектора. Угол между этими векторами и называется углом между векторами . Возьмем любую точку и приложим к ней оба вектора. Угол между этими векторами и называется углом между векторами 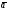 и и 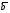 . Традиционно выбирается тот угол, который меньше . Традиционно выбирается тот угол, который меньше 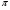 . .Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение: 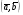 или или 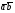 . .Итак, 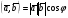 , ,где 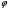 - угол между векторами - угол между векторами 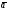 и и 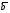 . .Так как 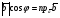 , ,то можно записать, что 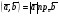 или 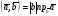 . .Свойства скалярного произведения.
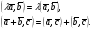 37. Векторное произведение векторов и его свойства Определние: Вектор c называется векторным произведением векторов a и b, обозначается c=[a,b], если |c|=|a|*|b|*sin(a^b), c перпендикулярен a и b, abc- правая тройка. Cвойства векторного произведения: 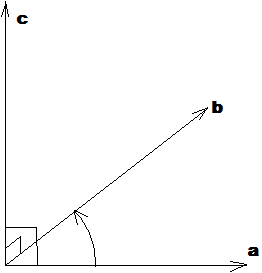 1)[a,b]=-[b,a] 2)[w*a,b]=[a,w*b]=w*[a,b] 3)[a+b,c]=[a,c]+[b,c] 4)[a,a]=0 Определение. Тройка некомпланарных векторов 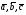 называется правой (положительно ориентированной), если после приведения к общему началу вектор называется правой (положительно ориентированной), если после приведения к общему началу вектор 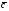 лежит по ту сторону плоскости, определяемой векторами лежит по ту сторону плоскости, определяемой векторами 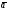 и и 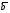 , откуда кратчайший поворот от вектора , откуда кратчайший поворот от вектора 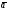 к вектору к вектору 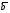 кажется совершаемым против часовой стрелки (в положительном направлении). В противном случае тройка векторов называется левой (отрицательно ориентированной). кажется совершаемым против часовой стрелки (в положительном направлении). В противном случае тройка векторов называется левой (отрицательно ориентированной). Иначе, тройка некомпланарных векторов называется правой (левой), если находясь внутри телесного угла, образованного приведенными к общему началу векторами 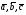 , мы видим поворот от , мы видим поворот от 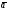 к к 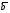 и затем от и затем от 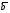 к к 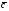 совершающимся против часовой стрелки (по часовой стрелке). совершающимся против часовой стрелки (по часовой стрелке).Из данных трех векторов 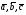 можно составить шесть различных упорядоченных троек. Три из них ( можно составить шесть различных упорядоченных троек. Три из них (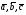 ; ; 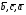 ; ; 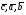 ) являются правыми, остальные три ( ) являются правыми, остальные три (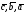 ; ; 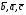 ; ; 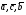 ) являются левыми. ) являются левыми. Определение. Векторным произведением векторов 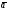 и и 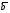 называется вектор называется вектор 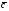 , удовлетворяющий следующим условиям: , удовлетворяющий следующим условиям:1) вектор 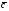 ортогонален ортогонален 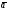 и и 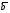 ; ;2) векторы образуют правую тройку; 3) длина вектора 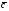 равна произведению длин векторов равна произведению длин векторов 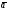 и и 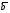 на синус угла между ними: на синус угла между ними: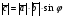 . .Обозначение: 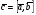 или или 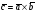 . .Очевидные геометрические свойства векторного произведения: векторы 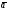 и и 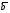 коллинеарны коллинеарны  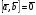 . .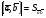 , где , где 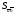 - площадь параллелограмма, построенного на векторах - площадь параллелограмма, построенного на векторах 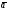 и и 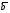 . .38. Смешанное произведение векторов и его геометрический смысл 9.4. Смешанное произведение трех векторов. Пусть даны три произвольных вектора 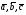 . . Определение. Смешанным произведением 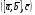 векторов векторов 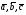 называется скалярное произведение векторного произведения называется скалярное произведение векторного произведения 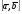 на вектор на вектор 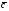 . .Геометрический смысл смешанного произведения показывает следующая теорема. Теорема 2. Смешанное произведение 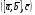 равно объему параллелепипеда, построенного на векторах равно объему параллелепипеда, построенного на векторах 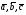 , приведенных к общему началу, взятому со знаком плюс, если тройка векторов , приведенных к общему началу, взятому со знаком плюс, если тройка векторов 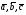 правая, и минус в противном случае. Если векторы правая, и минус в противном случае. Если векторы 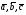 компланарны, то смешанное произведение компланарны, то смешанное произведение 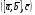 равно 0. равно 0. Доказательство. Если векторы 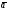 и и 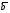 коллинеарны, то их векторное произведение равно нулю и, следовательно, смешанное произведение коллинеарны, то их векторное произведение равно нулю и, следовательно, смешанное произведение 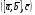 равно нулю. равно нулю.Пусть 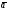 и и 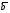 не коллинеарны. Обозначим через не коллинеарны. Обозначим через 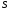 площадь параллелограмма, построенного на приведенных к общему началу векторах площадь параллелограмма, построенного на приведенных к общему началу векторах 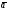 и и 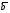 , а через , а через 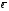 орт векторного произведения орт векторного произведения 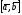 . Тогда: . Тогда: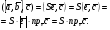 Если векторы 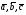 некомпланарны, то с точностью до знака некомпланарны, то с точностью до знака 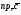 равна высоте параллелепипеда, построенного на векторах равна высоте параллелепипеда, построенного на векторах 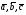 , при условии, что параллелограмм, поостренный на векторах , при условии, что параллелограмм, поостренный на векторах 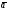 и и 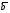 , является основанием этого параллелепипеда. Следовательно, с точностью до знака смешанное произведение равно объему этого параллелепипеда. Остается разобраться со знаком. , является основанием этого параллелепипеда. Следовательно, с точностью до знака смешанное произведение равно объему этого параллелепипеда. Остается разобраться со знаком.Если тройка векторов 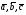 является правой, т.е. вектор является правой, т.е. вектор 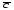 лежит по ту же сторону плоскости, определяемой векторами лежит по ту же сторону плоскости, определяемой векторами 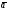 и и 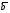 , что и вектор , что и вектор 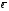 , то проекция , то проекция 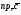 положительна. Если тройка векторов положительна. Если тройка векторов 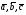 является левой, т.е. вектор является левой, т.е. вектор 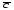 лежит по другую сторону плоскости, то проекция лежит по другую сторону плоскости, то проекция 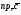 отрицательна. отрицательна. Наконец, если векторы 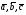 компланарны, то вектор компланарны, то вектор 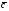 лежит в плоскости, определяемой векторами лежит в плоскости, определяемой векторами 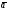 и и 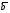 , и его проекция на направление вектора , и его проекция на направление вектора 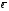 равна 0. Значит, равно 0 и смешанное произведение равна 0. Значит, равно 0 и смешанное произведение 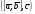 . Теорема доказана. . Теорема доказана.39. Смешанное произведение векторов : Свйосвта и вычесление Вычисление смешанного произведения в декартовых координатах. Теорема. Если в декартовой прямоугольной системе координат 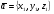 , , 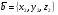 , , 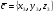 , ,то 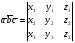 . .Доказательство. По определению смешанного произведения 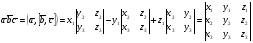 . .Теорема доказана. Следствие 1. Справедливо равенство 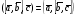 . . Действительно, 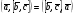 в силу коммутативности скалярного произведения. Значит, нам надо показать, что в силу коммутативности скалярного произведения. Значит, нам надо показать, что 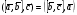 . С точностью до знака обе части равенства равны объему параллелепипеда, построенного на векторах . С точностью до знака обе части равенства равны объему параллелепипеда, построенного на векторах 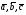 . А знак их совпадает, поскольку тройки векторов . А знак их совпадает, поскольку тройки векторов 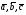 и и 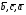 имеют одинаковую ориентацию. имеют одинаковую ориентацию.Равенство 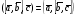 позволяет записывать смешанное произведение просто в виде позволяет записывать смешанное произведение просто в виде 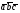 , не учитывая, какие именно вектора участвуют в векторном произведении. , не учитывая, какие именно вектора участвуют в векторном произведении.Следствие 2. Для компланарности трех векторов необходимо и достаточно равенство нулю их смешанного произведения. Смешанное произведение кососимметрично по отношению ко всем своим аргументам: т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и : 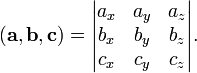 В частности, Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю. Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой. 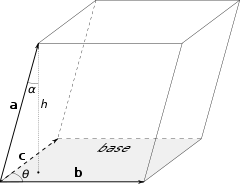 Три вектора, определяющие параллелепипед. |

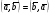 .
.