Ответы на экзаменационные билеты_2. Матрицы. Операции сложения матриц и умножения матриц на число. Транспонирование матриц. Операция умножения матриц и её свойства
 Скачать 318.5 Kb.
|
Определение. Матрицей размера mxn называется прямоугольная таблица чисел, состоящая из m строк и n столбцов. А числа 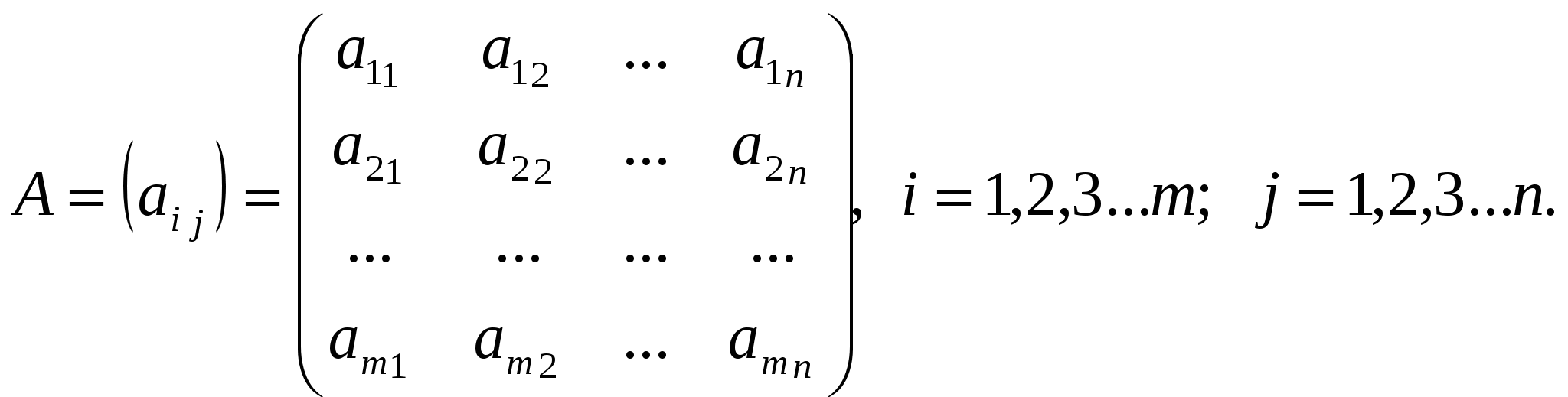 называются элементами матрицы А. Операции над матрицами.
 Свойства:    
 Свойства:    
 Свойства:   
 Свойства: 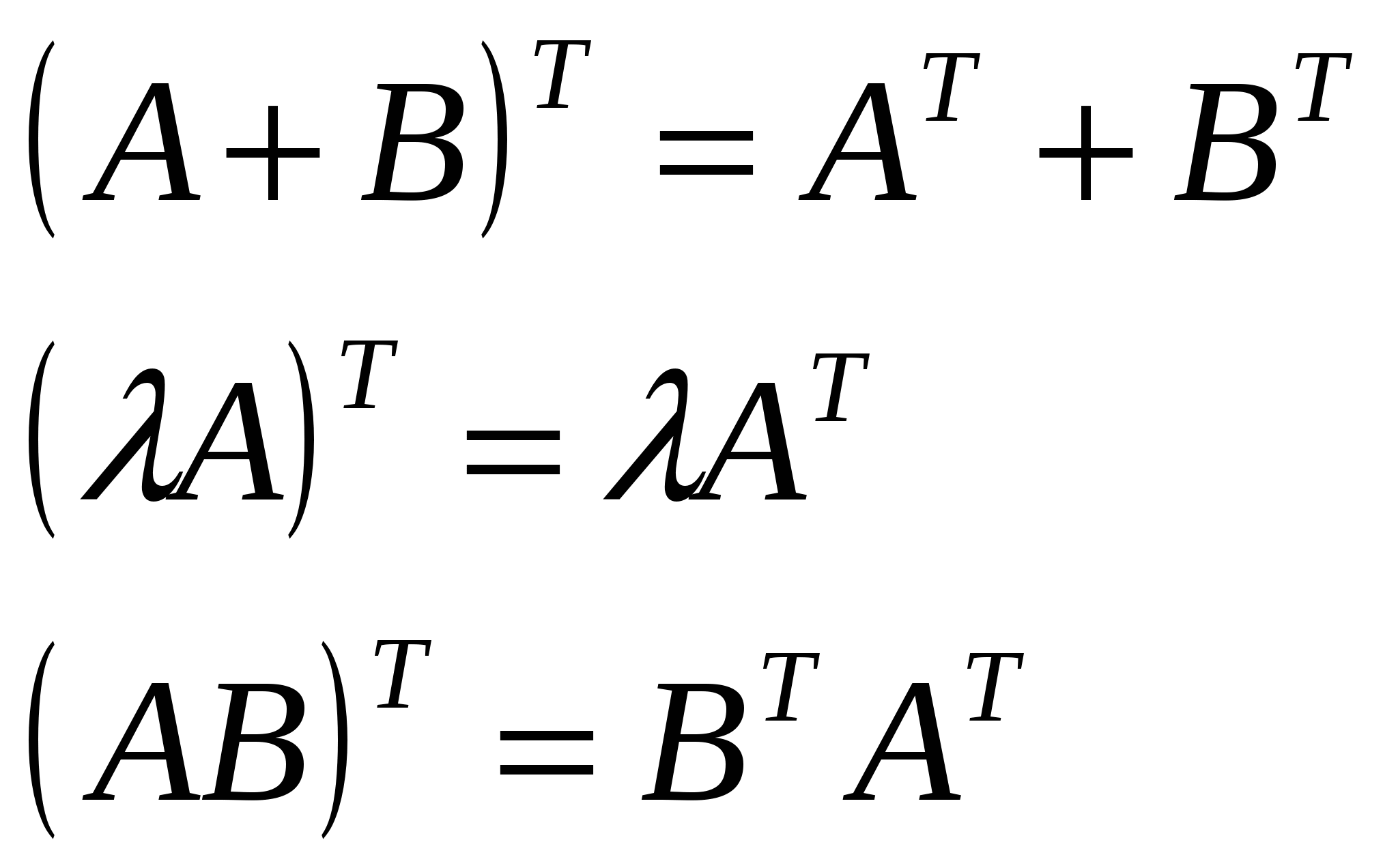 Виды матриц.
Определение. Всякое расположение чисел  в некотором определённом порядке называется перестановкой из n чисел (символов). Общий вид перестановки  .Всякое взаимно однозначное отображение A множества первых n натуральных чисел на себя называется подстановкой. Общий вид подстановки 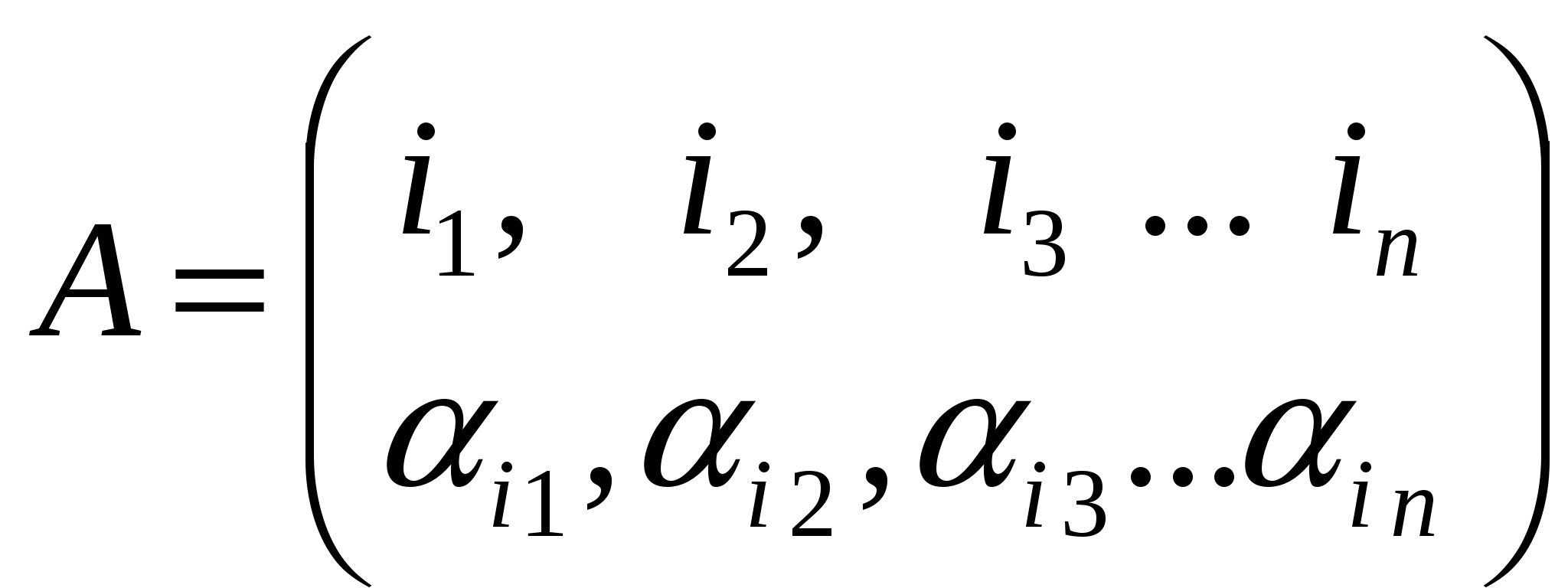 .Свойства перестановок и подстановок.
Определение. Определителем (или детерминантом) матрицы 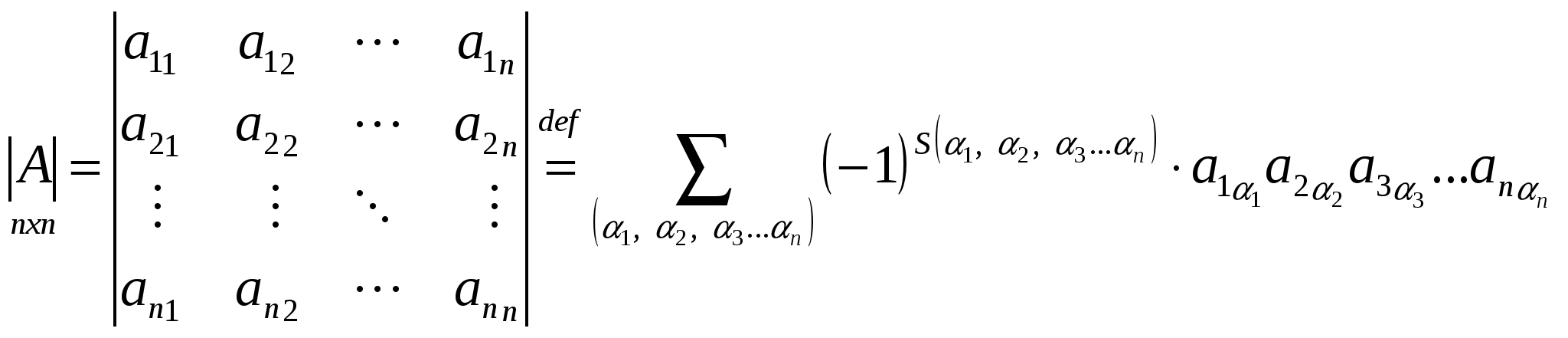 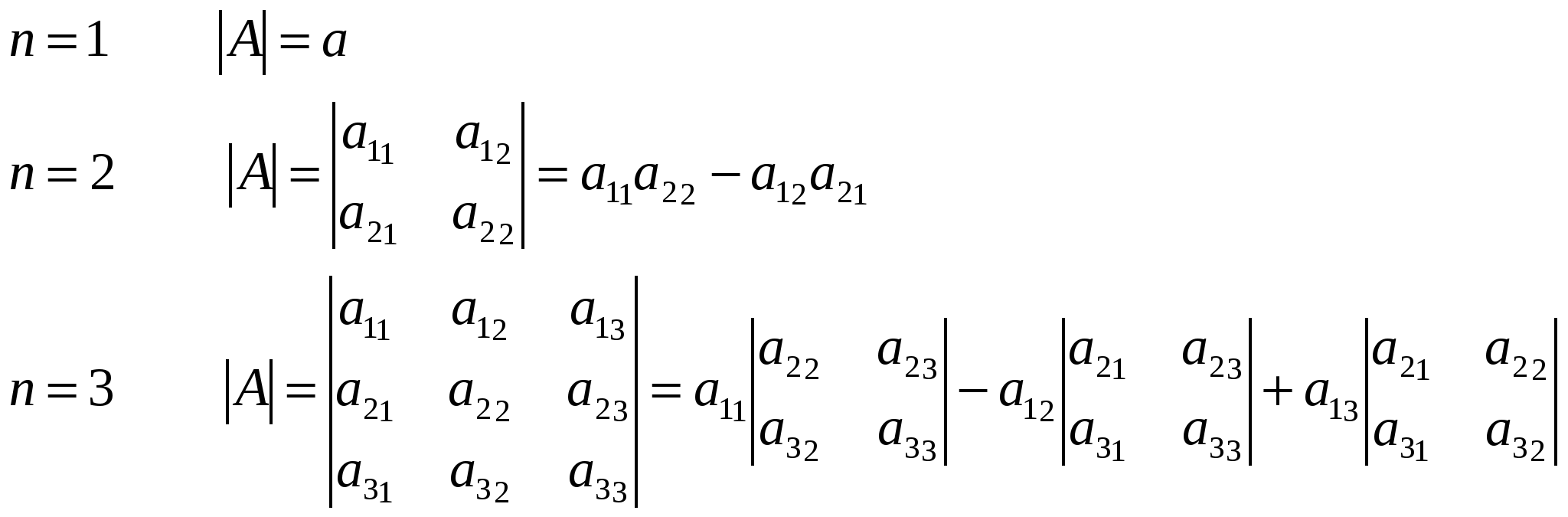называется число, которое ставится в соответствие этой матрице и может быть вычислено по её элементам по формуле  – перестановка из чисел   – число инверсий в перестановке  Определитель транспонированной матрицы. При транспонировании матрицы её определитель не меняется, т. е.  . Отсюда следует, что любое утверждение, справедливое для столбцов, будет справедливо и для строк определителя матрицы.Доказательство.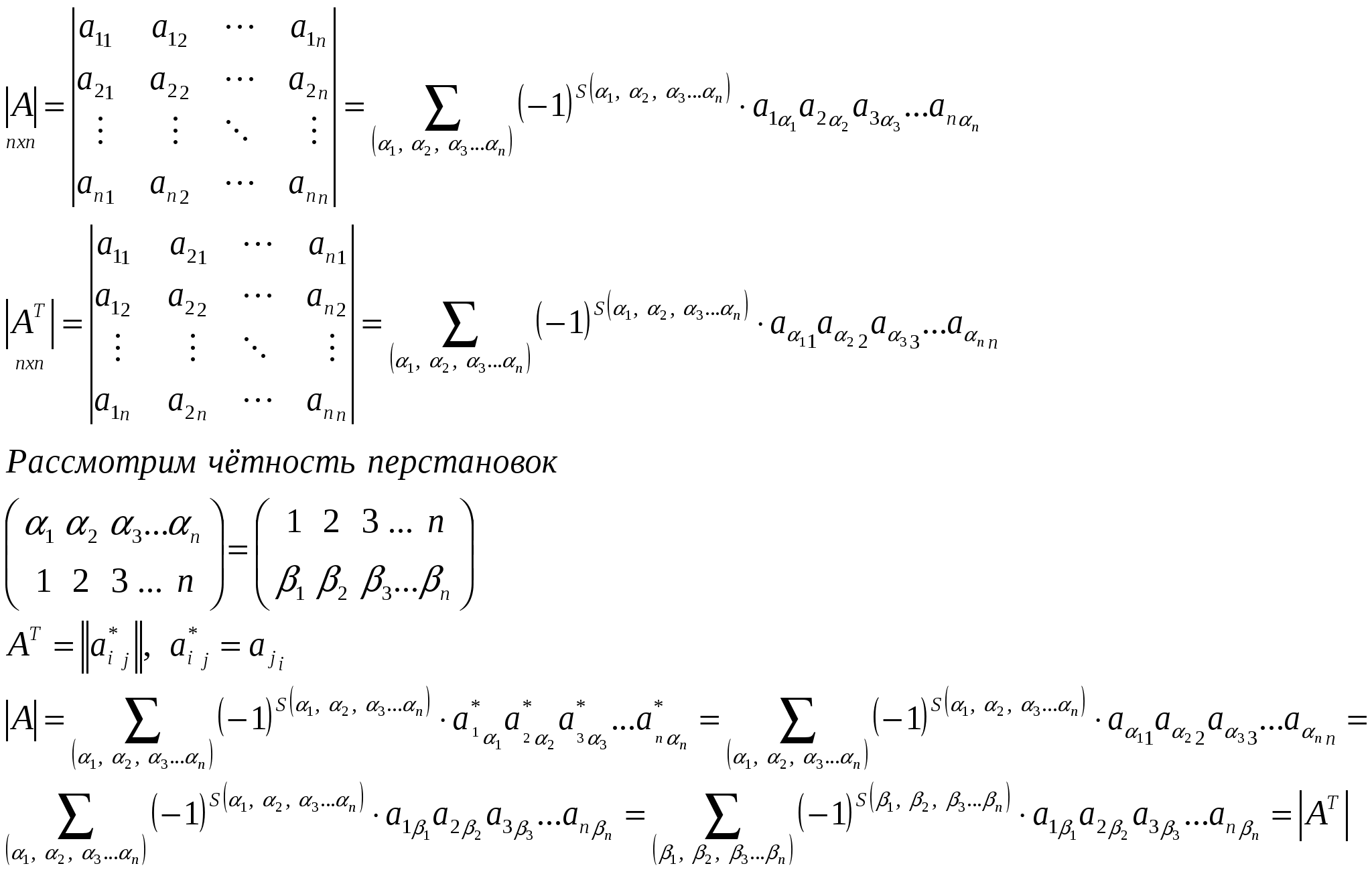 
Свойства определителя:
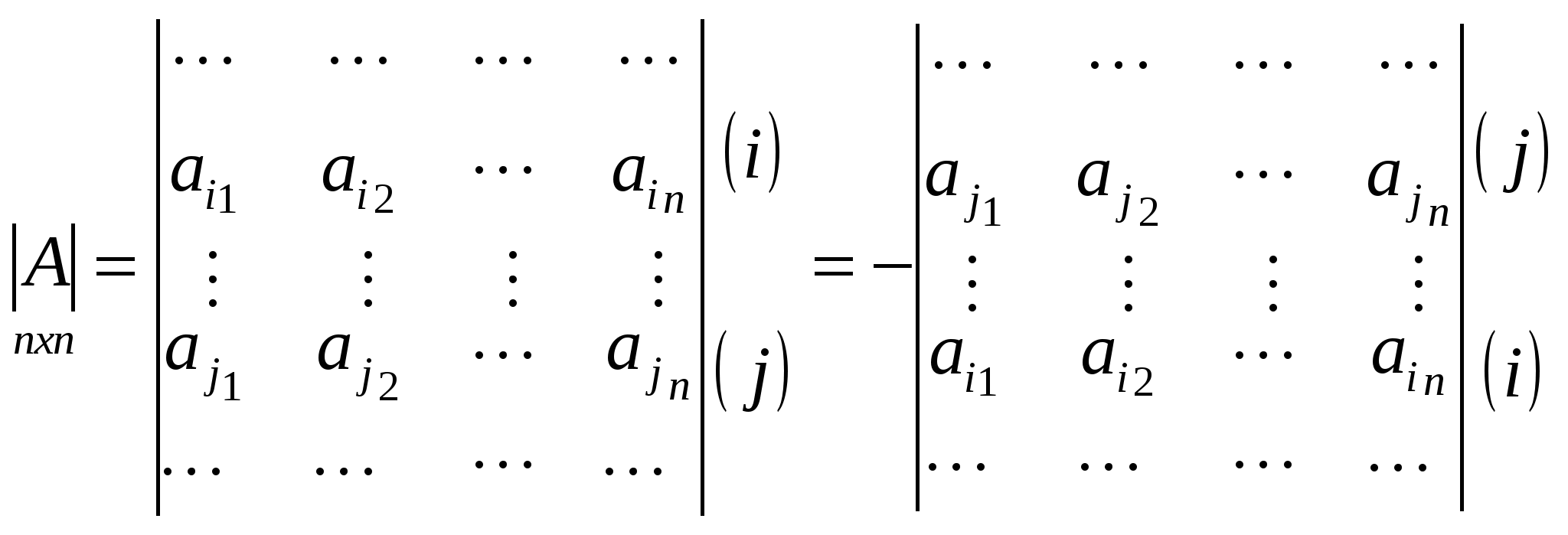 Доказательство.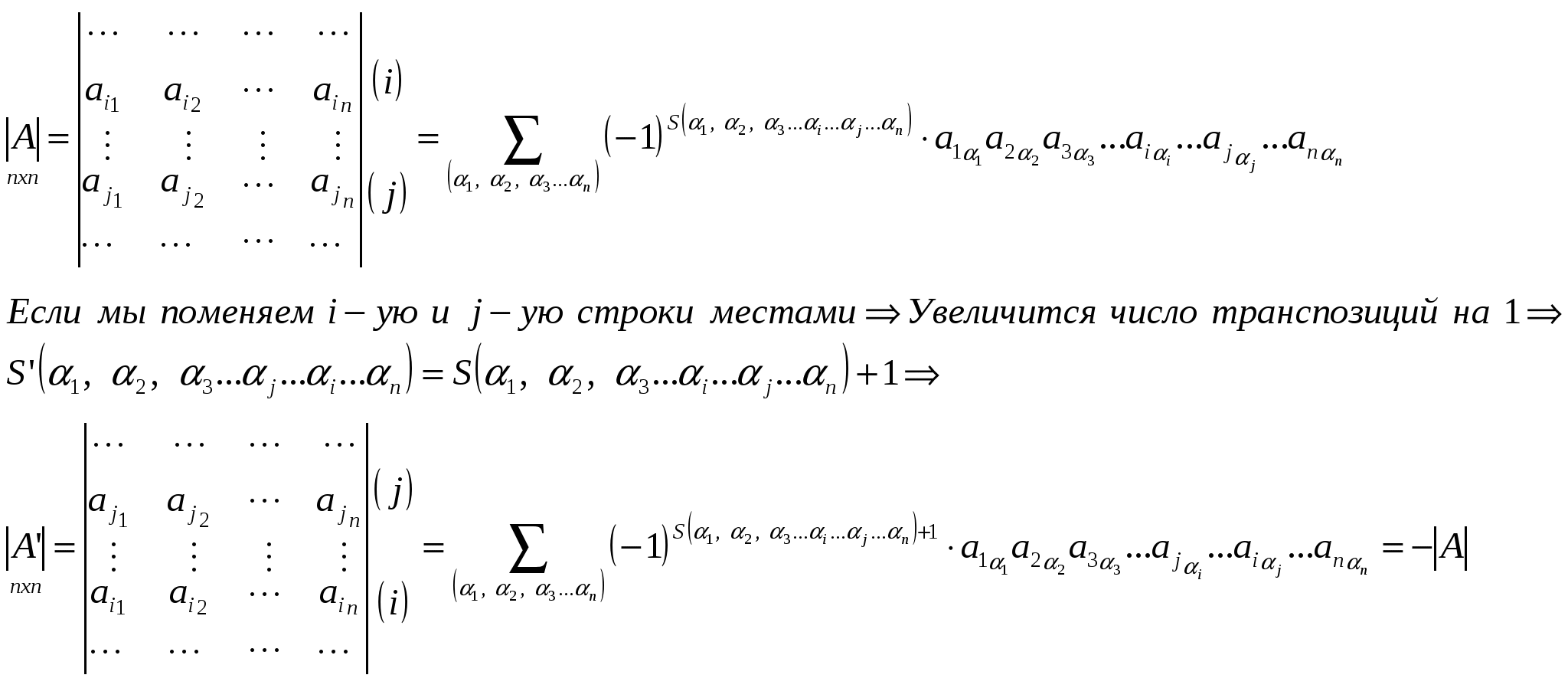 
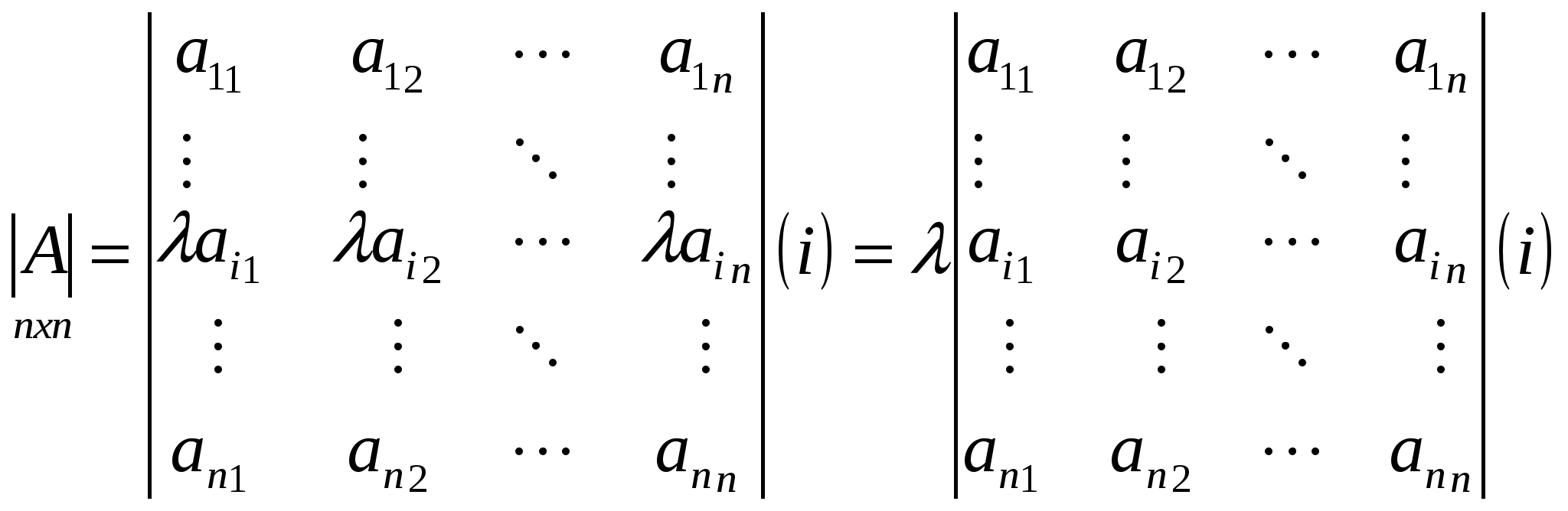 Доказательство. 
 Доказательство.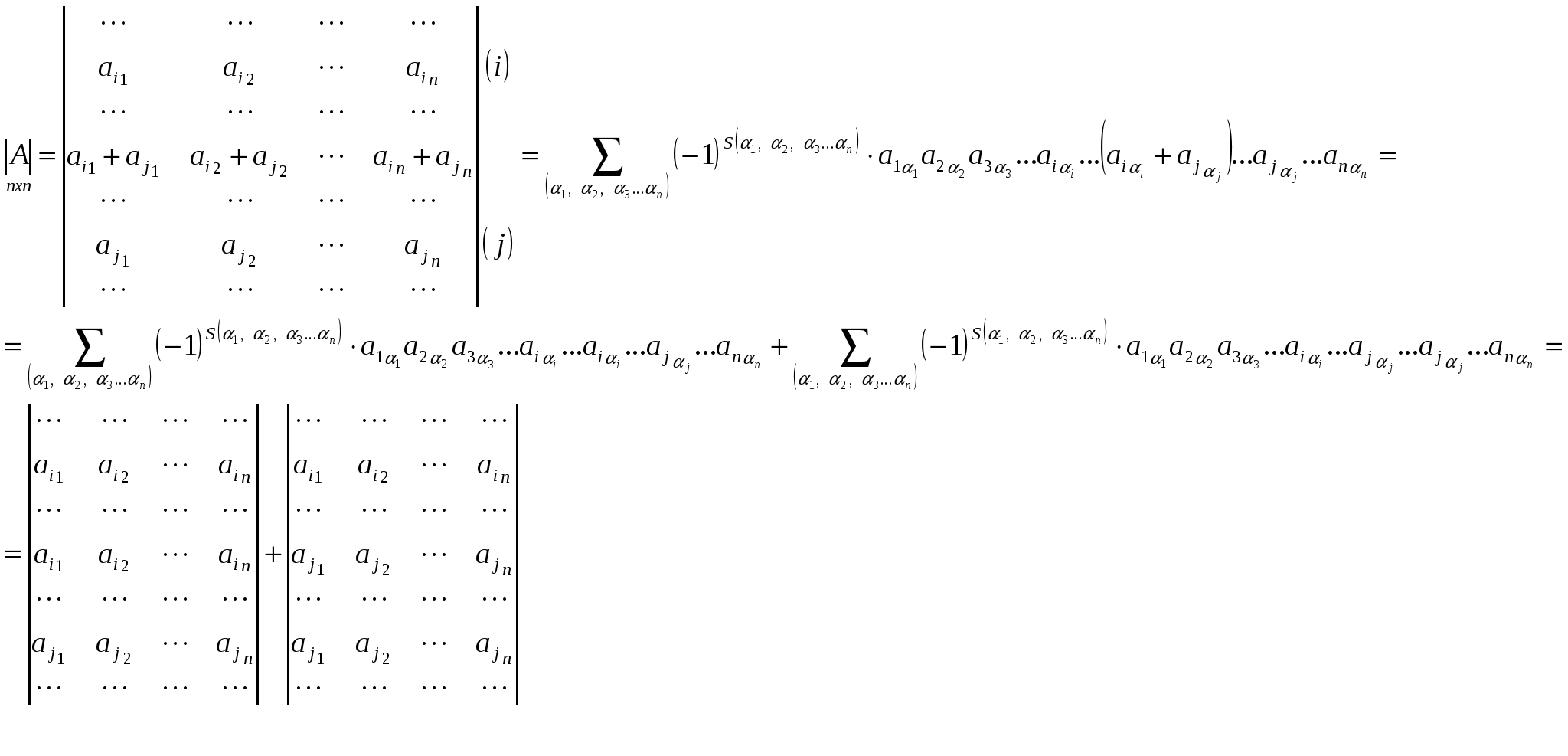 
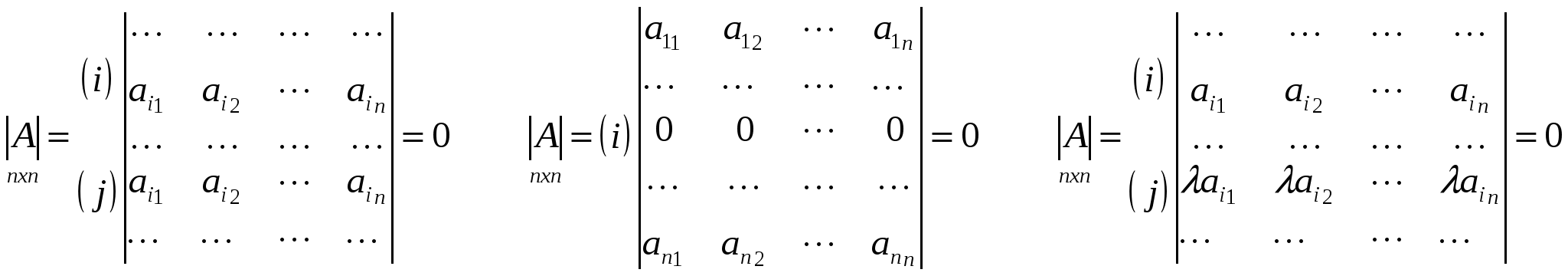
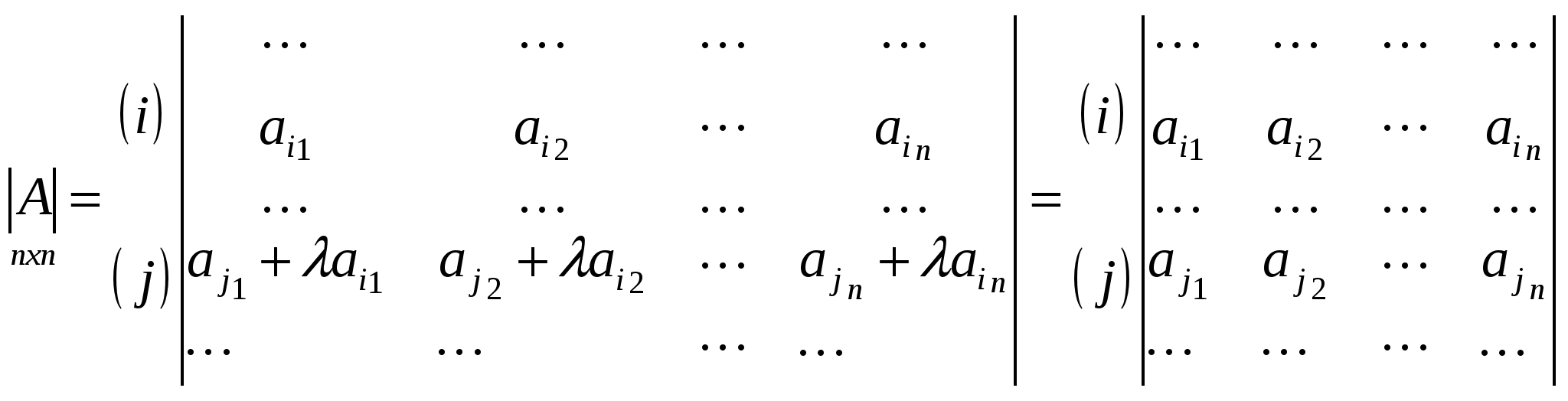
Определение. Минором матрицы k-ого порядка называется определитель матрицы, состоящей из элементов, расположенных на пересечении k строк и k столбцов ( 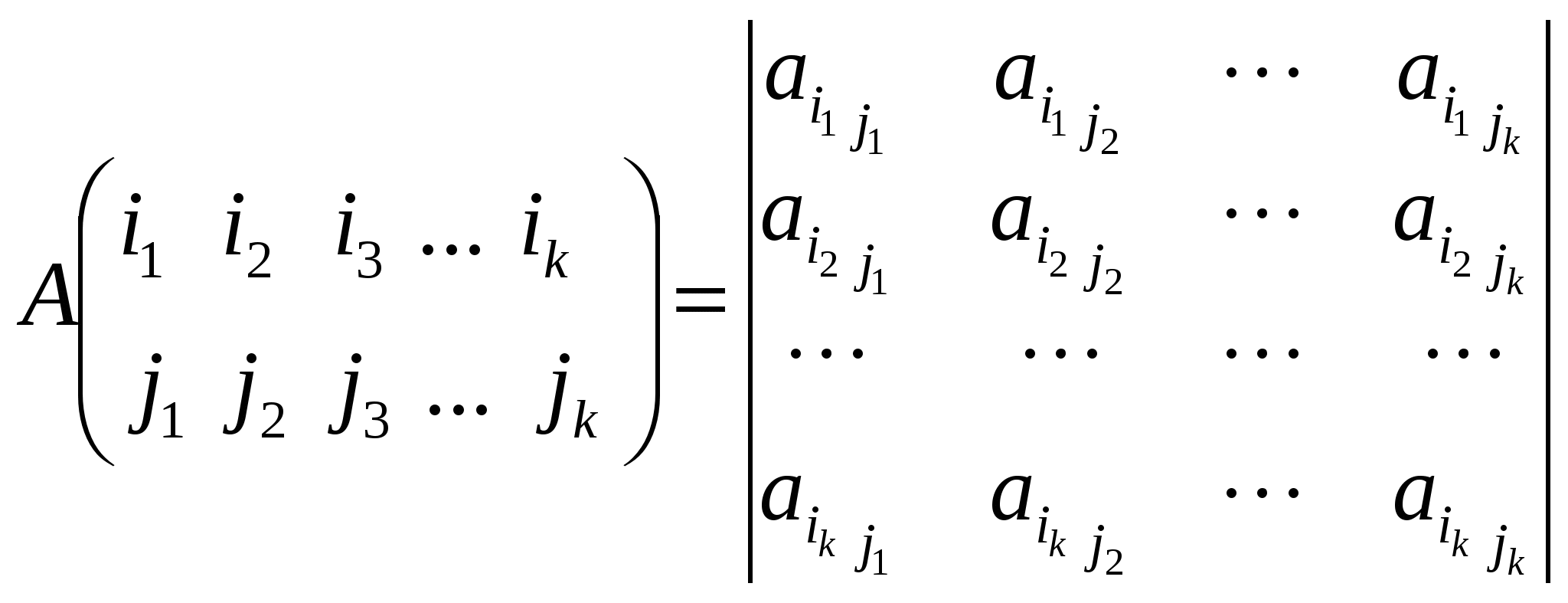 ) данного определителя d порядка n. Пусть в определителе d n-ого порядка взят минор M k-ого порядка. Если вычеркнуть те строки и столбцы, на пересечении которых стоит этот минор, то останется минор M’ (n–k)-ого порядка, который называется дополнительным минором для минора М. 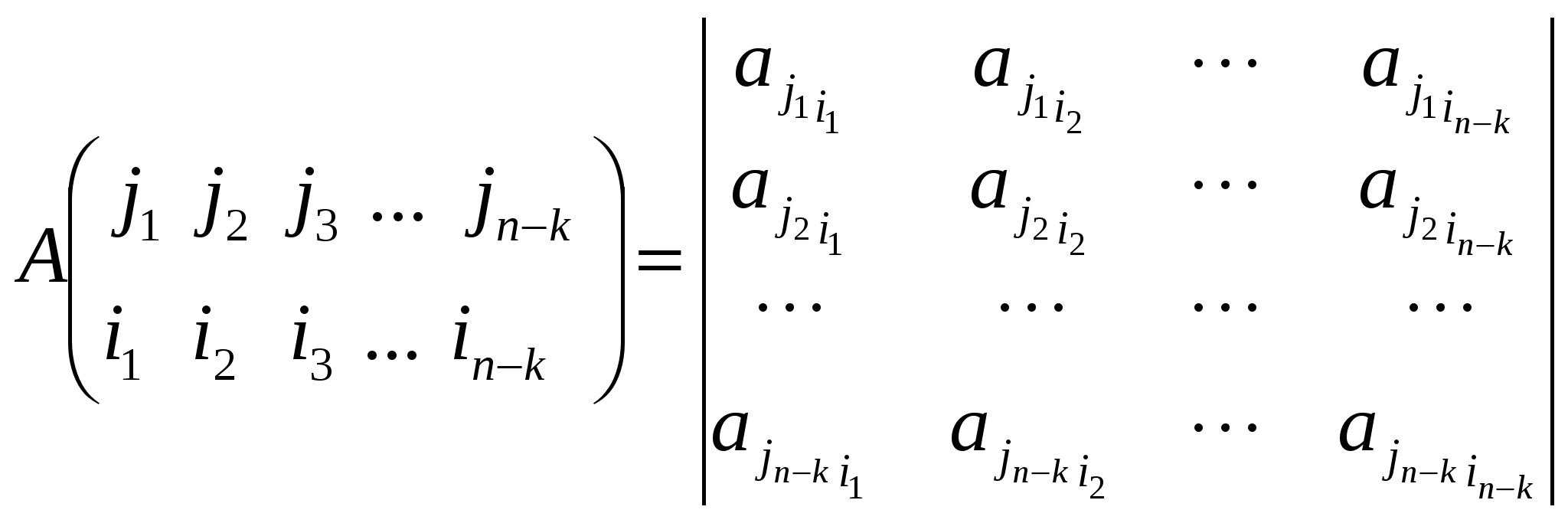 Если минор k-ого порядка расположен в строках с номерами 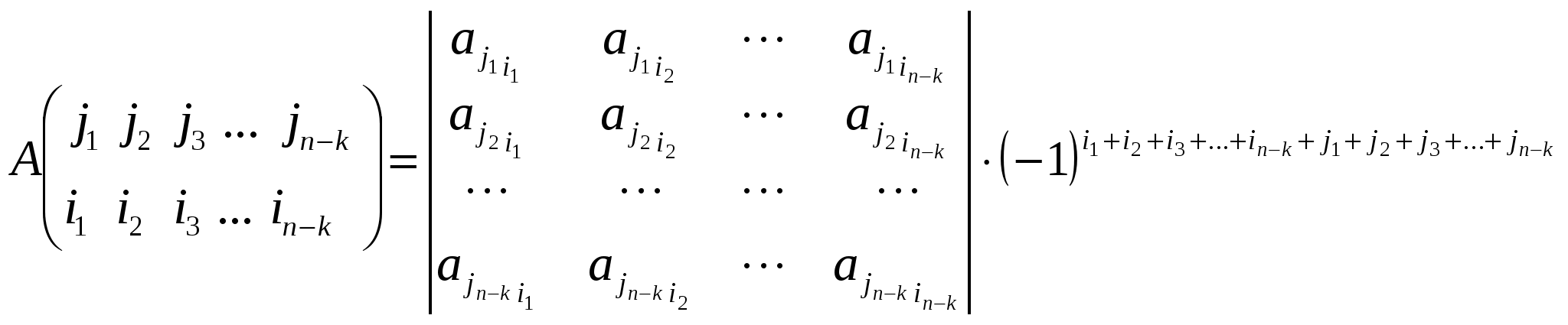 и столбцах с номерами  , то алгебраическим дополнением минора М является дополнительный минор М’, взятый со знаком  . Теорема. Произведением любого минора k-ого порядка матрицы А на его алгебраическое дополнение состоит из слагаемых, представляющих собой члены определителя матрицы А с правильным знаком. Доказательство.
Теорема. Пусть в определителе d порядка n произвольно выбраны k строк (или k столбцов), . Тогда сумма произведений всех миноров k-ого порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна определителю d. 
Определение. Разложение определителя 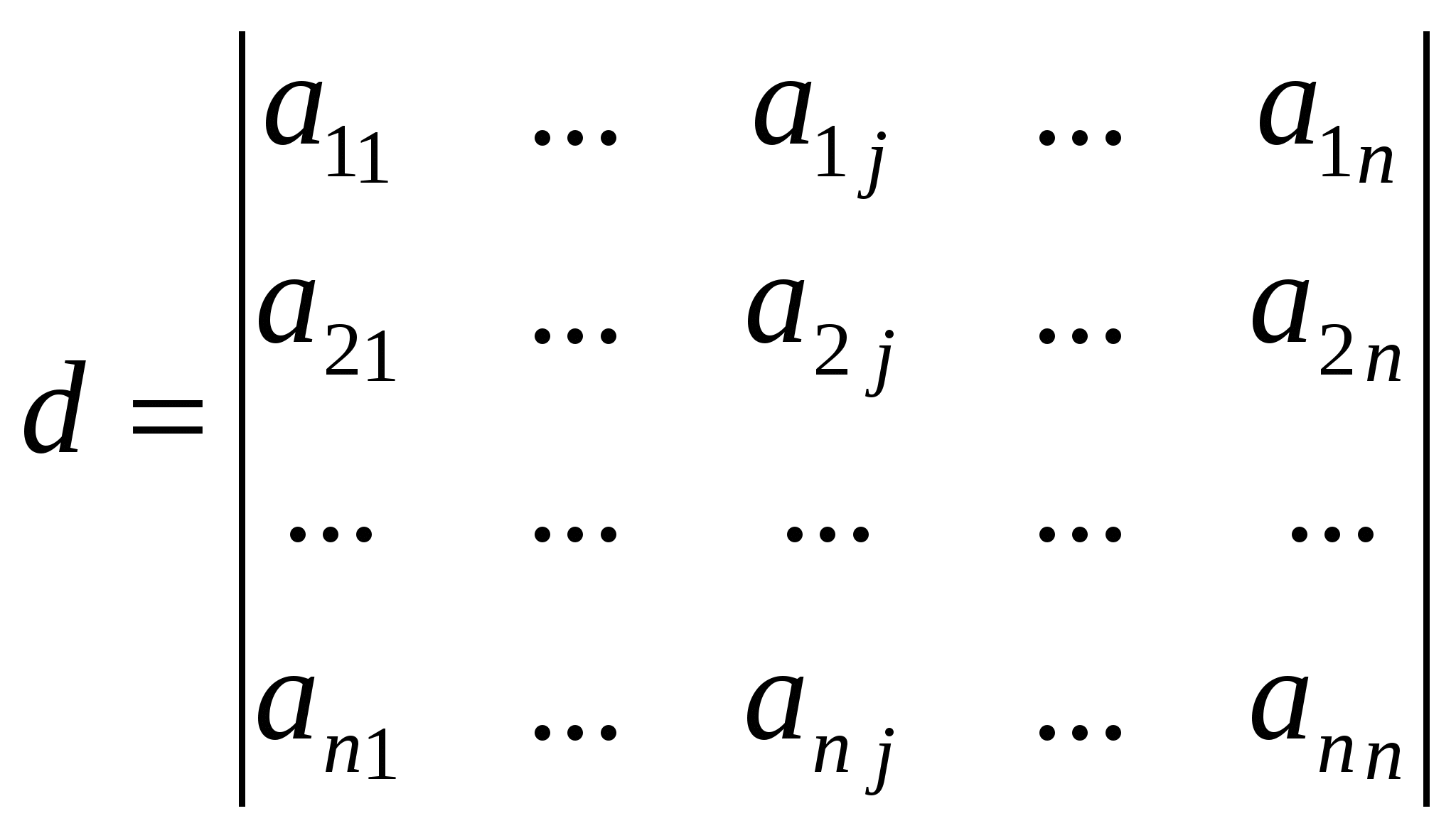 по j-ому столбцу  .Теорема. Сумма произведений всех элементов некоторого столбца (строки) определителя на алгебраические дополнения соответственных элементов другого столбца (строки) равна нулю, т. е.  .
Пусть дана система, определитель которой не равен нулю, вида 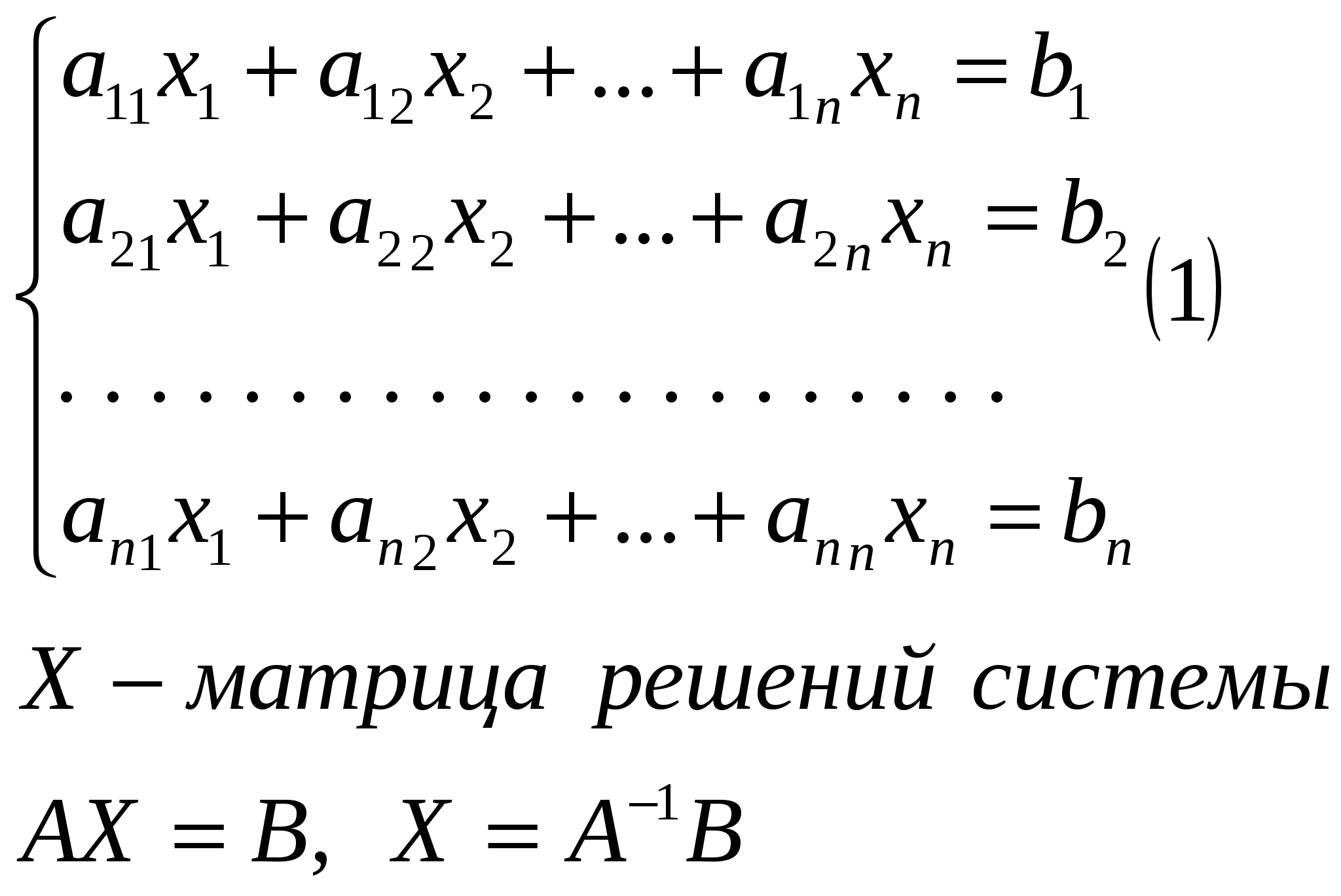 Правило Крамера. Система (1) однозначно разрешима при любых правых частях тогда и только тогда, когда определитель матрицы А не равен нулю. Это решение определяется формулой  , где  – определитель матрицы системы,  – определитель матрицы, получаемой из матрицы системы заменой i-ого столбца столбцом свободных членов.Доказательство.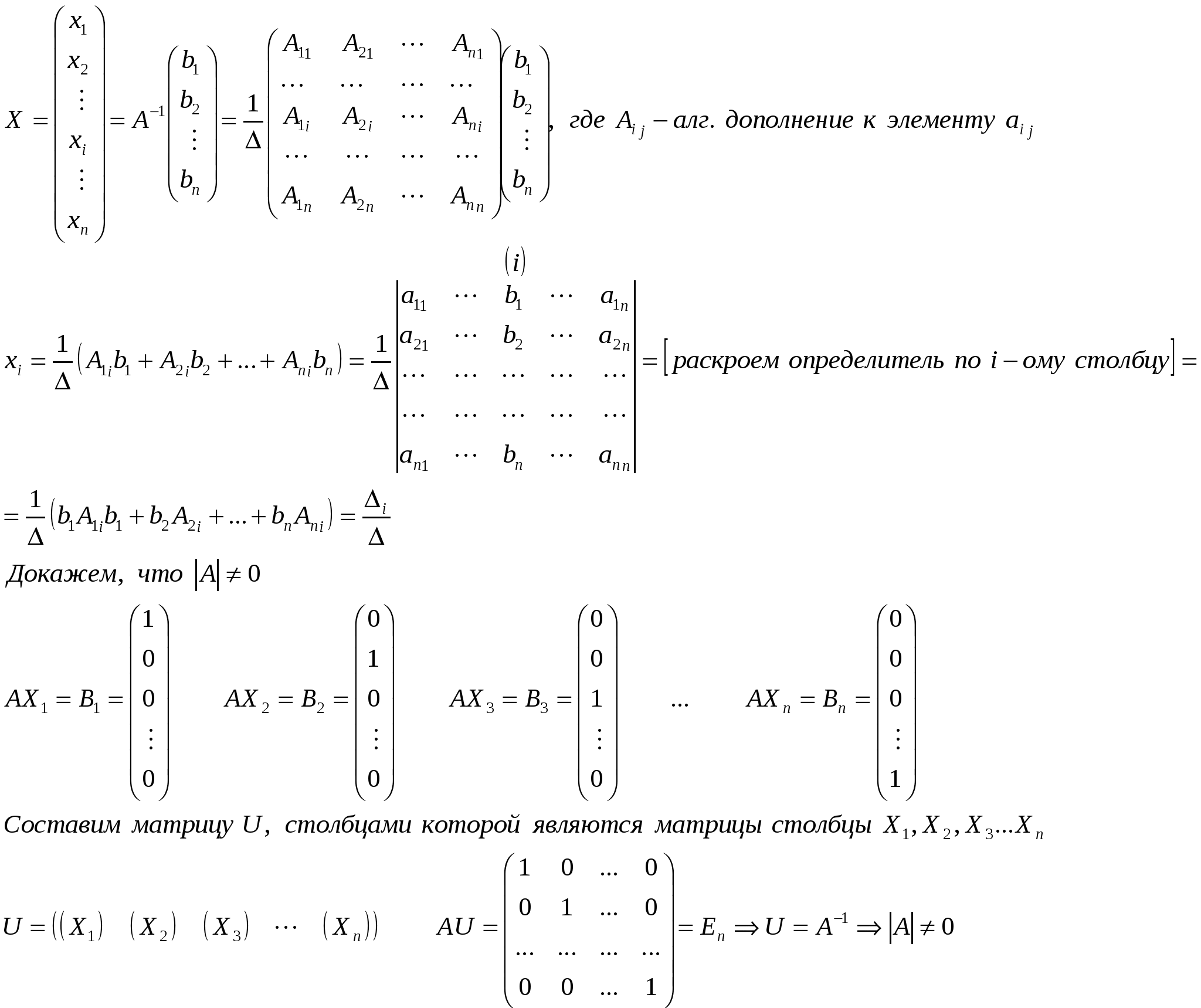 
Определение. Матрица B (A–1) называется обратной к матрице А, если АВ=ВА=Е (единичная матрица). Теорема.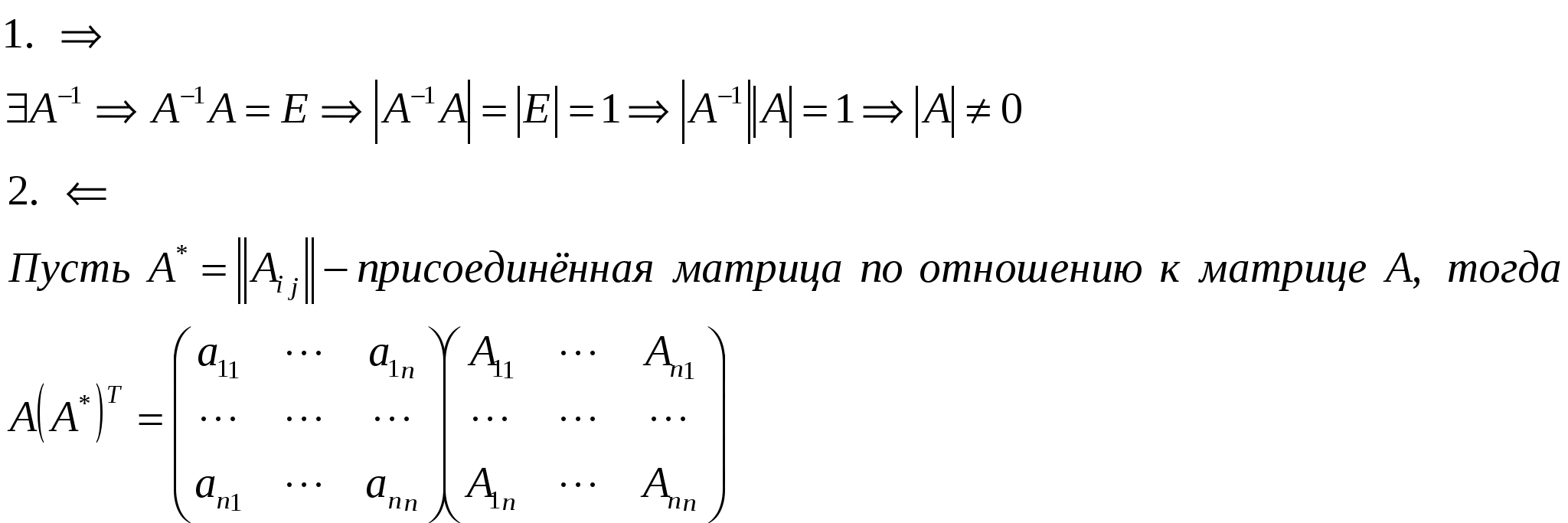  
Определение.  Определение. Минор, определяющий ранг матрицы, называется базисным минором. Строки и столбцы, формирующие базисный минор, называются базисными строками и столбцами. Определение. Система столбцов 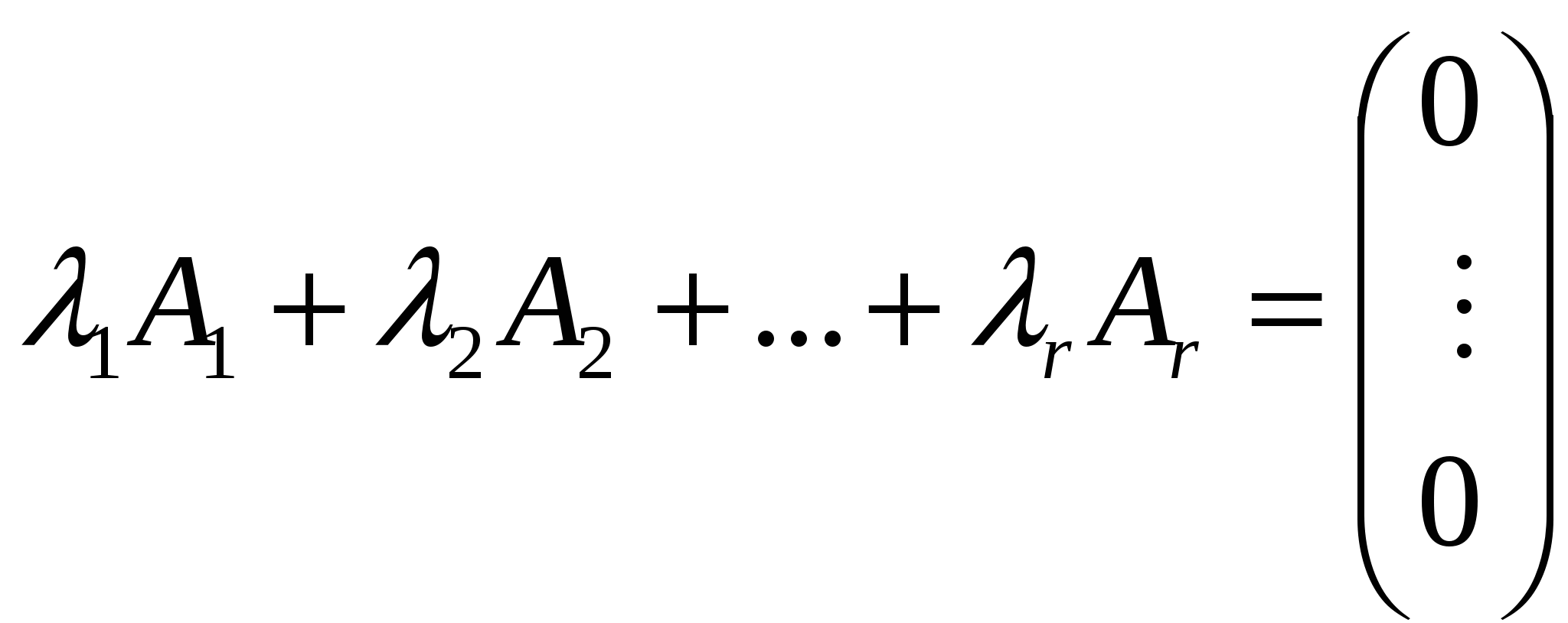 называется линейно зависимой  , не все равные нулю, и такие, что  Теорема. 1) Столбцы матрицы А, входящие в базисный минор, образуют линейно-независимую систему. 2) Любой столбец матрицы линейно выражается через столбцы базисного минора.  Доказательство. 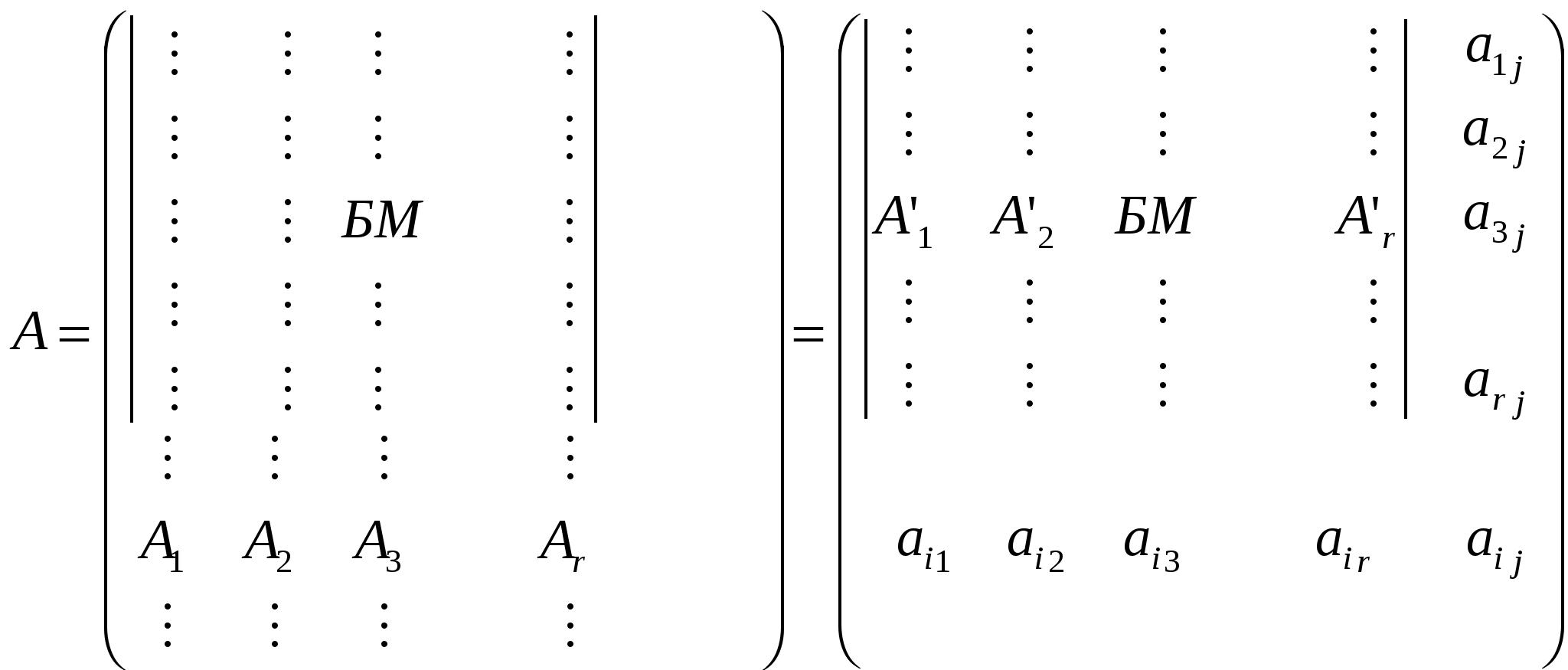  12. 13. Следствия из теоремы о базисном миноре. Следствия. а) Равенство определителя нулю.  Доказательство.  б) Линейная зависимость системы из (n+1) столбца размером из n элементов. 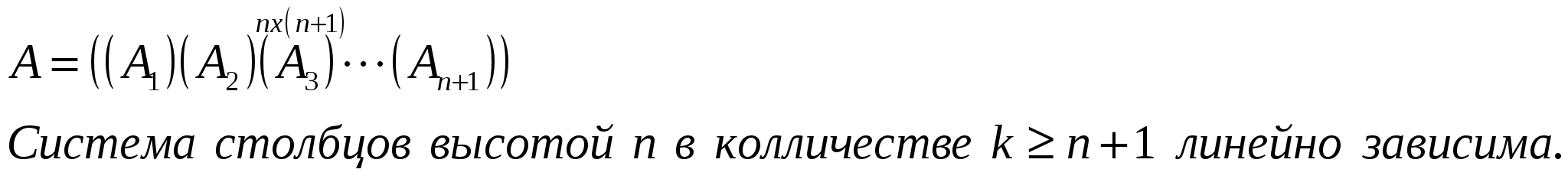 Доказательство.  в) Линейная независимость системы из k столбцов, линейно выражающихся через l столбцов.  Доказательство. 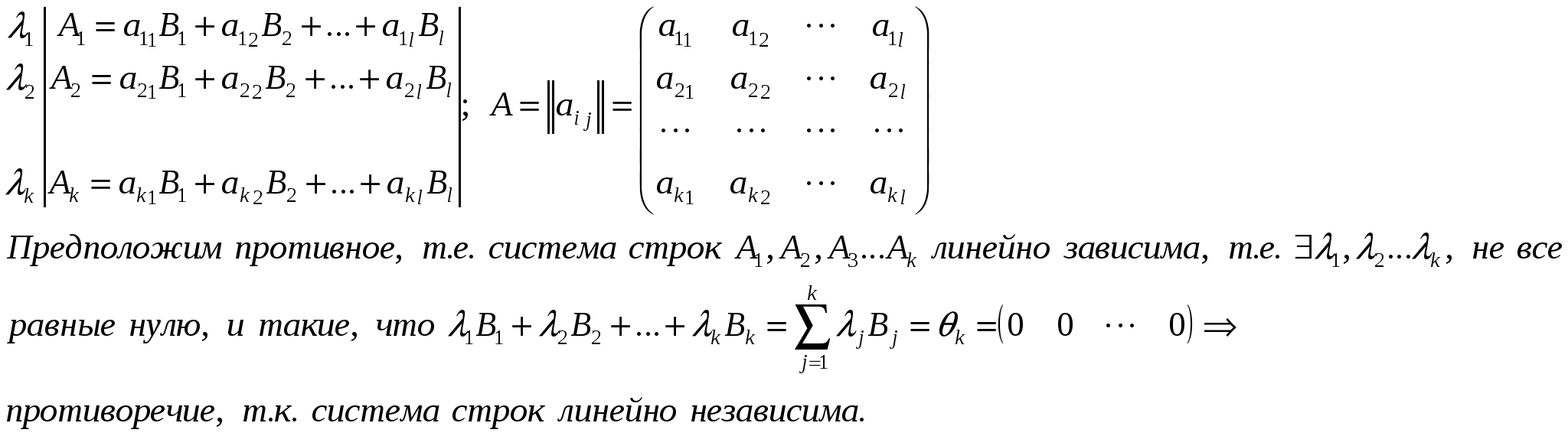 14. Теорема о ранге матрицы. Критерий линейной зависимости системы столбцов. Теорема. Ранг матрицы А равен числу столбцов (строк), входящих в максимальную линейно независимую подсистему. Доказательство. 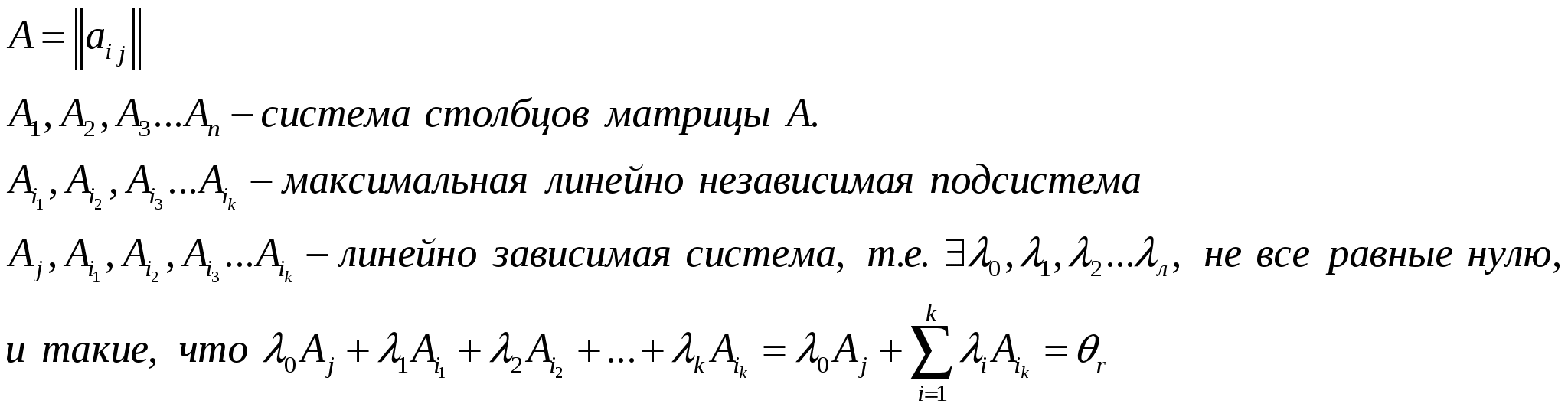 15. Метод окаймляющих миноров вычисления ранга матрицы. Теорема. Пусть минор k-ого порядка матриц А отличен от нуля, а все окаймляющие его миноры равны нулю, тогда ранг матрицы А равен k. Доказательство.  16. Элементарные преобразования, не изменяющие ранга матрицы. Теорема. Элементарные преобразования, не изменяющие ранга матрицы: 1. Умножение любой строки (столбца) на число отличное от нуля. 2. Перестановка любых двух строк (столбцов). 3. Прибавление к одной строке другой, умноженной на число. 4. Вычёркивание или приписывание нулевой строки. Доказательство.  17. Вычисление ранга матрицы методом Гаусса. Суть метода Гаусса заключается в привидении матрицы А к трапециевидной матрице путём зануления столбцов. 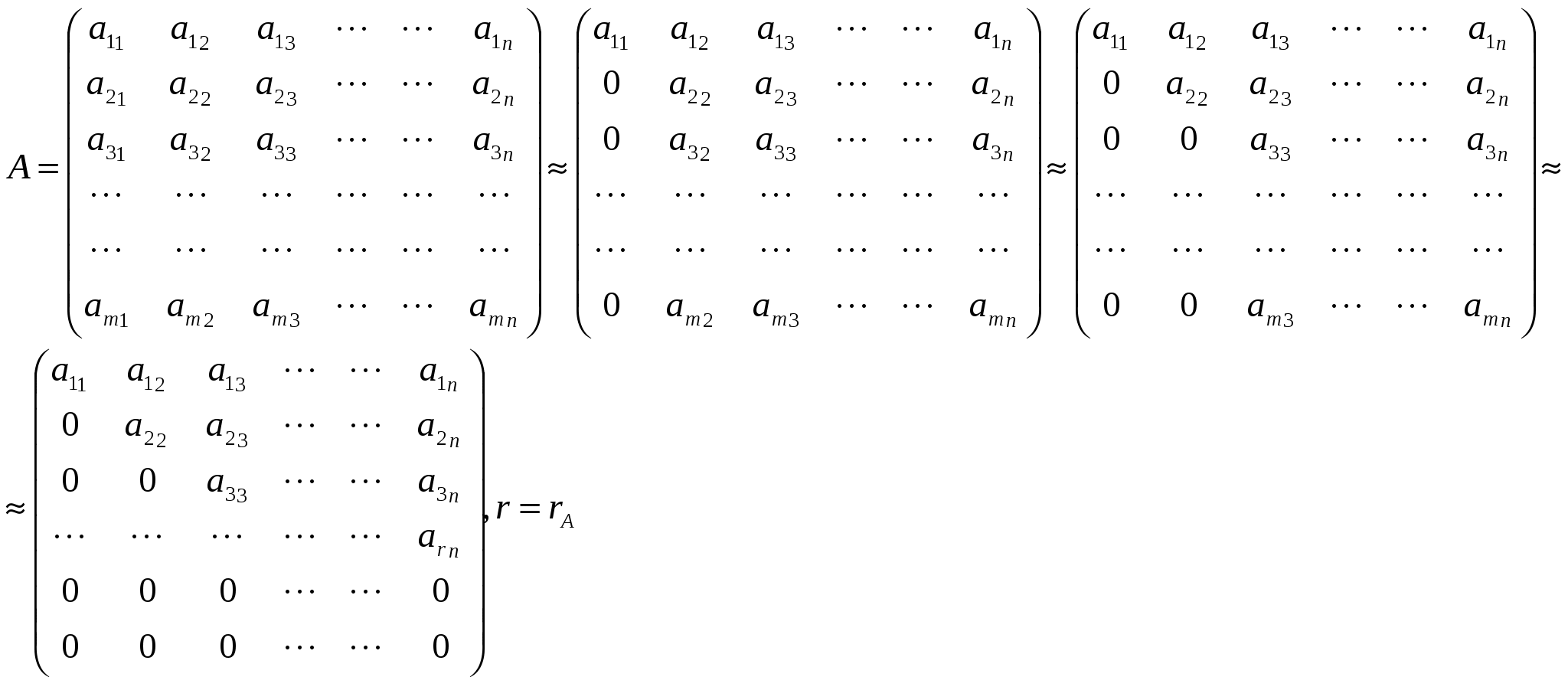 18. Теорема Кронекера-Капелли. Теорема. 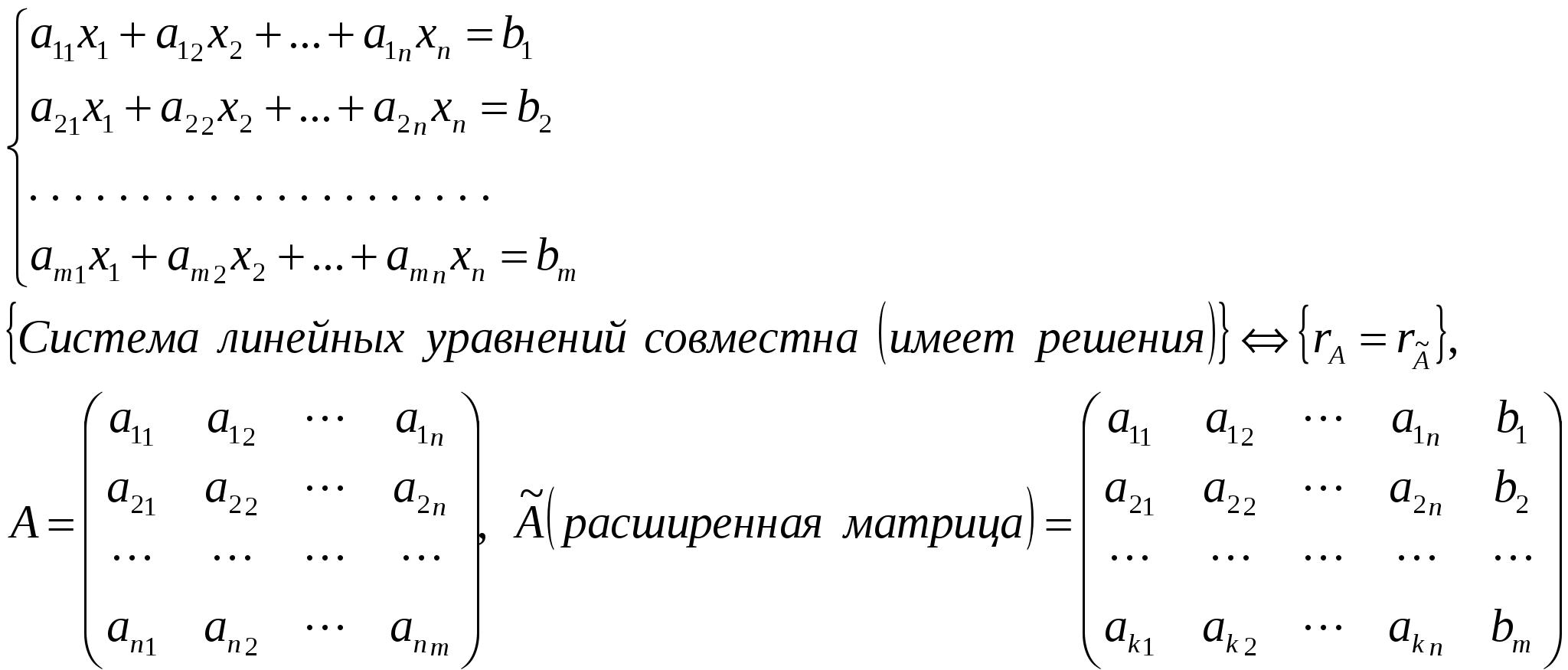 Доказательство.  23. Однородные системы линейных алгебраических дополнений: свойства решений, эквивалентное уравнение системы. 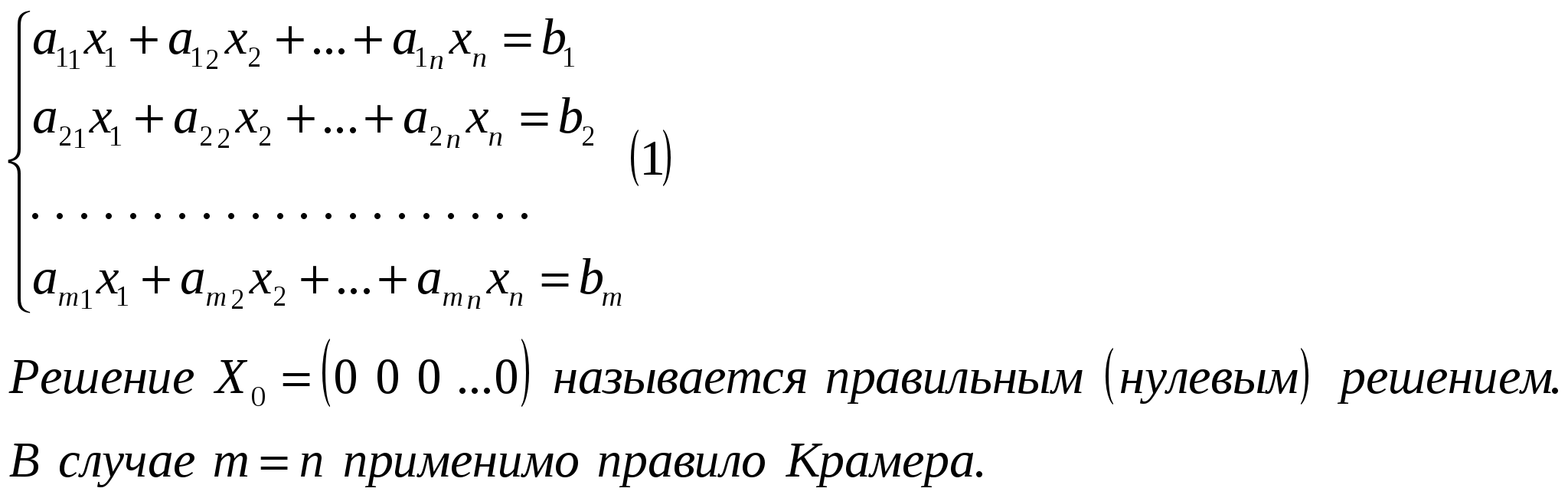 Определение. Урезанная система – система, из которой отброшены уравнения, у которой соответствующие им строки матрицы системы не входят в базисный минор. Утверждение. Урезанная система эквивалентна исходной системе, т. е. любые решения исходной системы равны решениям урезанной системы, и наоборот. Пример: 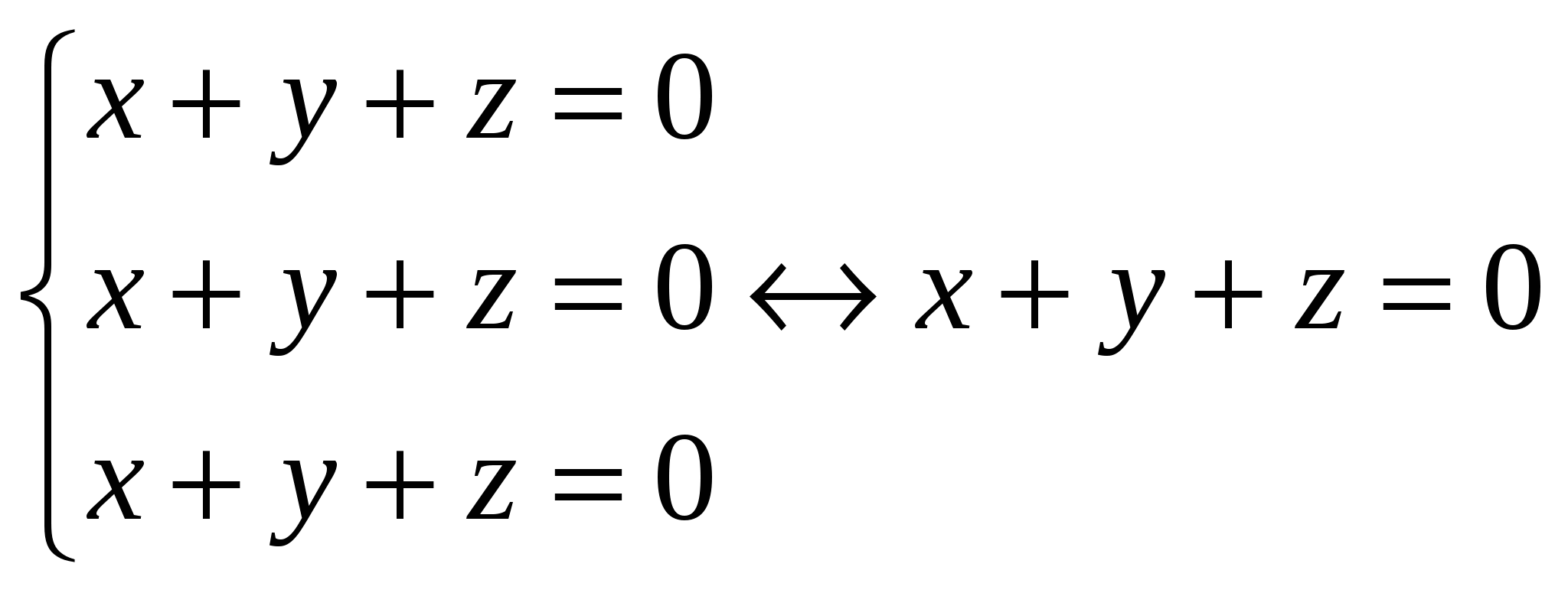 Доказательство. |
– матрица-строка (столбец);
– квадратная матрица;
– симметрическая матрица;
– кососимметричная матрица;
– нулевая матрица;
– противоположная матрица;
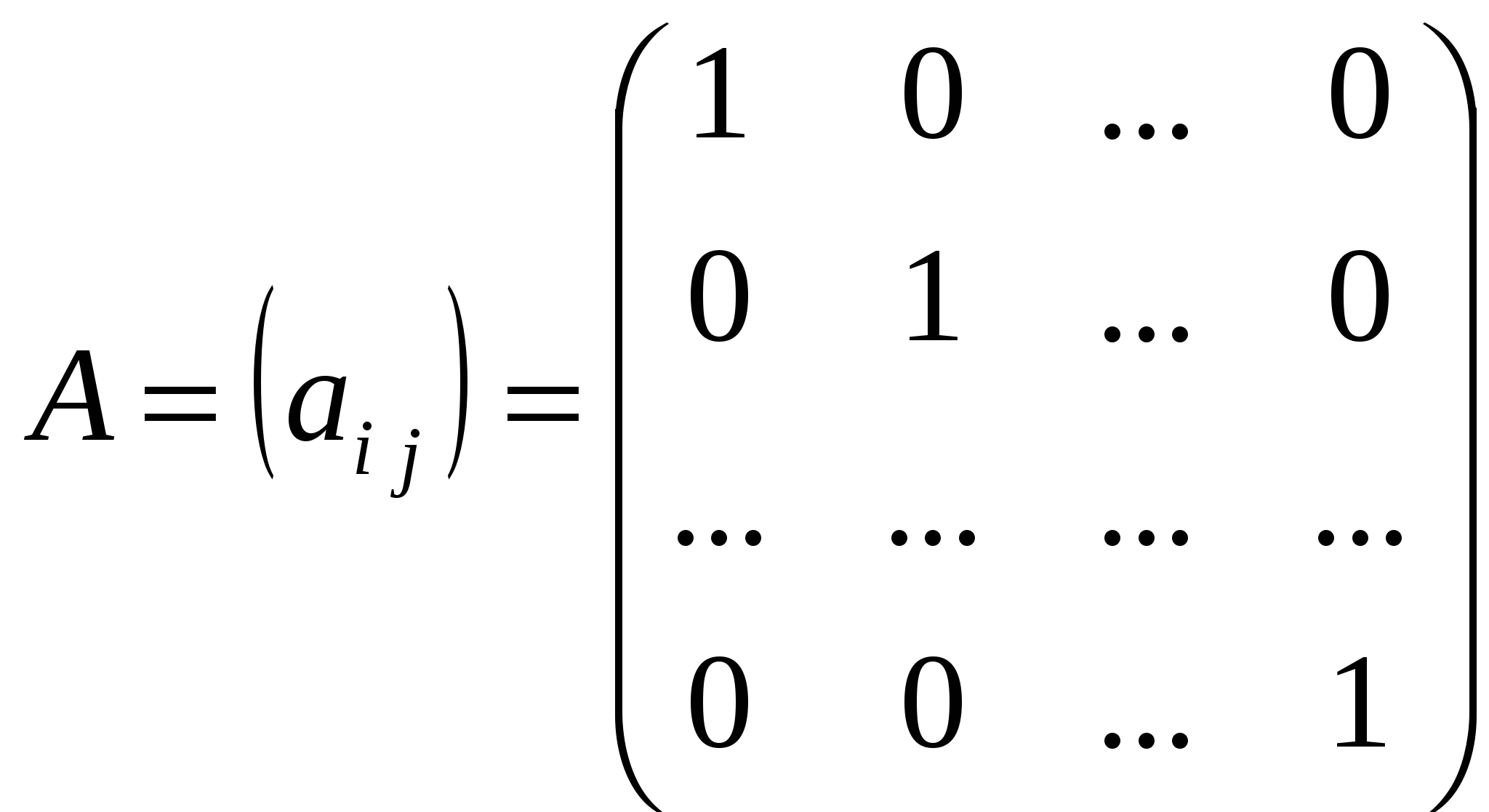– единичная матрица.
число чётных перестановок из n символов равно числу нечётных, т.е. 
n!