Для данного определителя найти миноры и алгебраические дополнения элементов a

• Название: Для данного определителя найти миноры и алгебраические дополнения элементов a
• Дата: 18.10.2021
• Размер: 98 Kb.
• Имя файла: 116_8v-IDZ1.1.doc
• Тип: Документы; #250377

ИДЗ 1.1 – Вариант 8
1. Для данного определителя Δ найти миноры и алгебраические дополнения элементов a_i2, a_3j. Вычислить определитель Δ: а) разложив его по элементам i-й строки; б) разложив его по элементам j-го столбца; в) получив предварительно нули в i-й строке.

1.8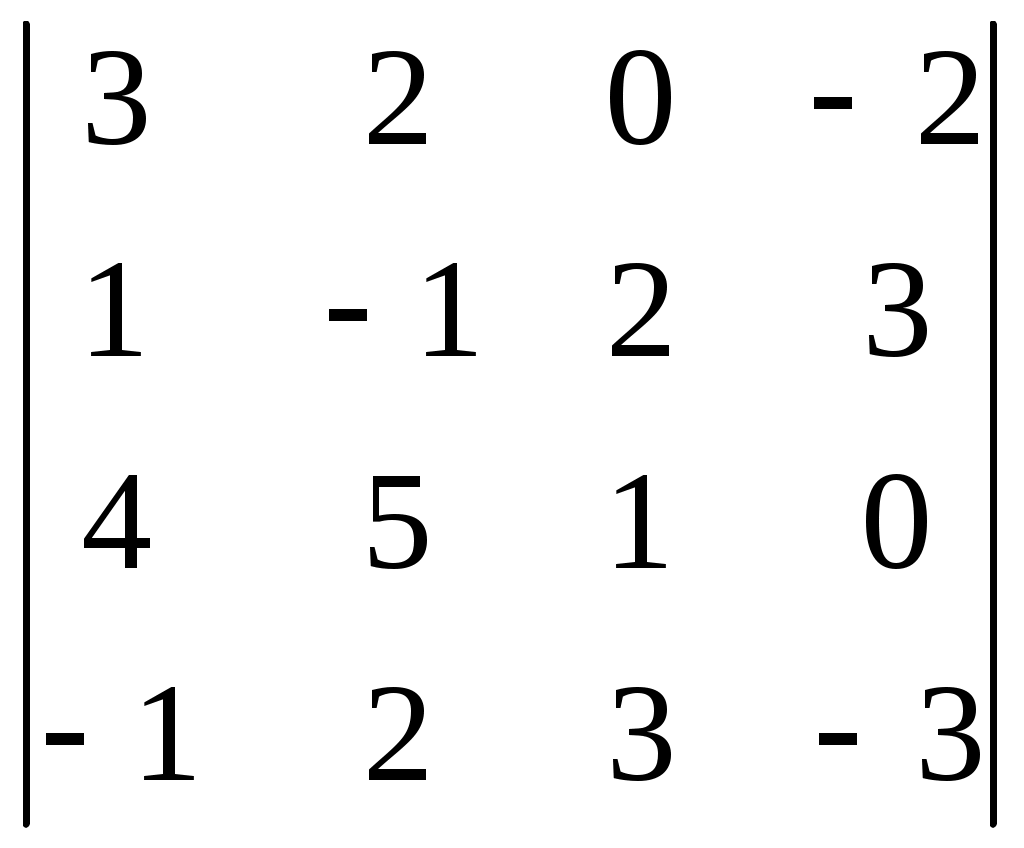

Алгебраическое дополнение A_ij элемента a_ij определяется равенством



Находим миноры: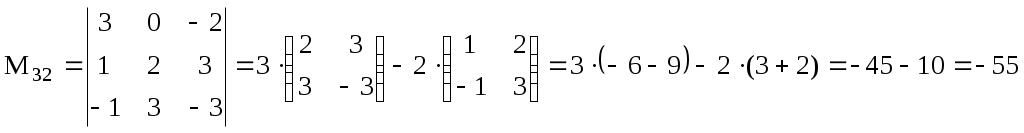





Алгебраические дополнения элементов а₃₂, и а₃₁ соответственно равны:



Вычислим определитель Δ: а) разложив его по элементам 3-й строки



Вычислим миноры по правилу треугольника:

Тогда определитель



Вычислим определитель Δ: б) разложив его по элементам 1-го столбца




Вычислим определитель Δ: в) получив предварительно нули в 3-й строке.

Умножим третий столбец на −4 и сложим с первым



умножим третий столбец на −5 и сложим со вторым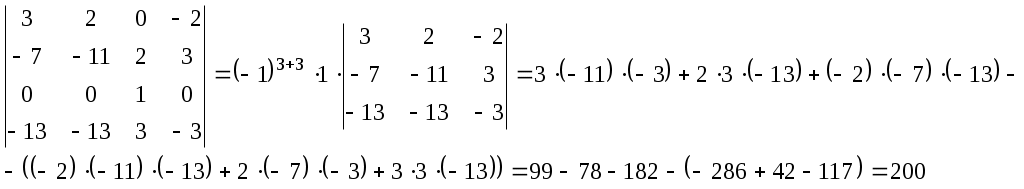






2. Даны две матрицы А и В. Найти: а) AB; б) BA; в) A⁻¹; г) AA⁻¹; д) A⁻¹A

2.8 ,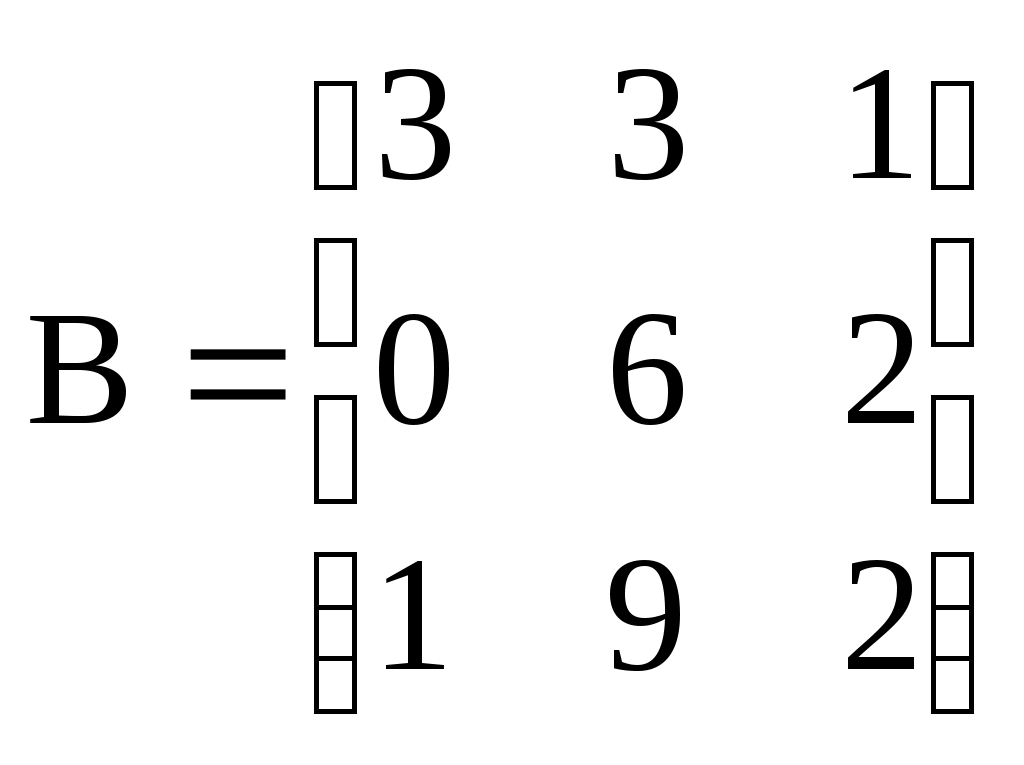
а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=AB, элементы которой

Имеем:


б)



Очевидно что

в) Найти: A⁻¹

Обратная матрица A⁻¹ матрицы А имеет вид: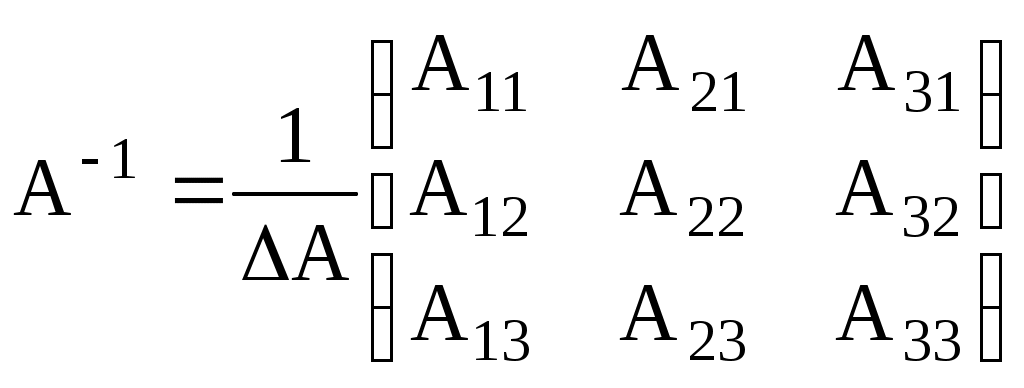



По правилу треугольника, вычислим определитель:





т.е. матрица А – невырожденная, и, значит, существует матрица A⁻¹.
Находим матрицу, состоящую из алгебраических дополнений элементов исходной матрицы: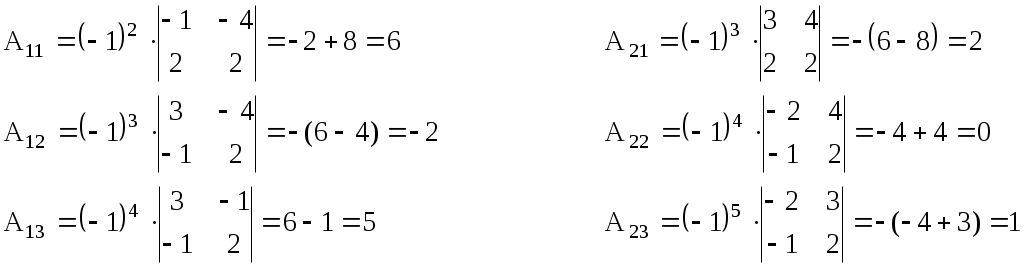





Таким образом получаем матрицу: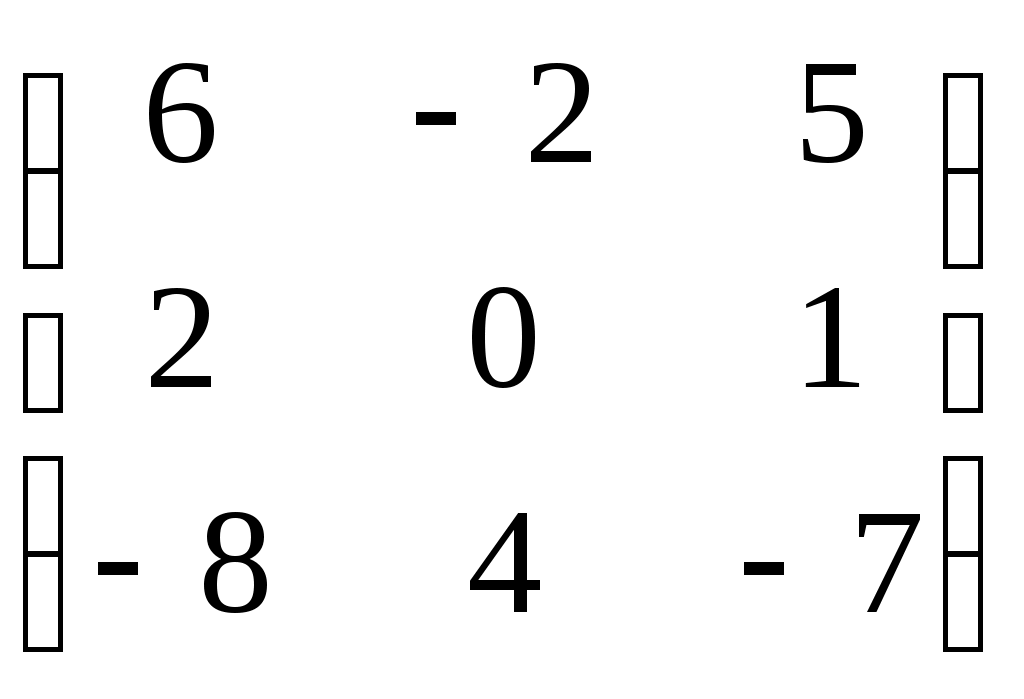



Полученную матрицу транспонируем:



Последнюю матрицу делим на определитель исходной матрицы и получаем обратную матрицу: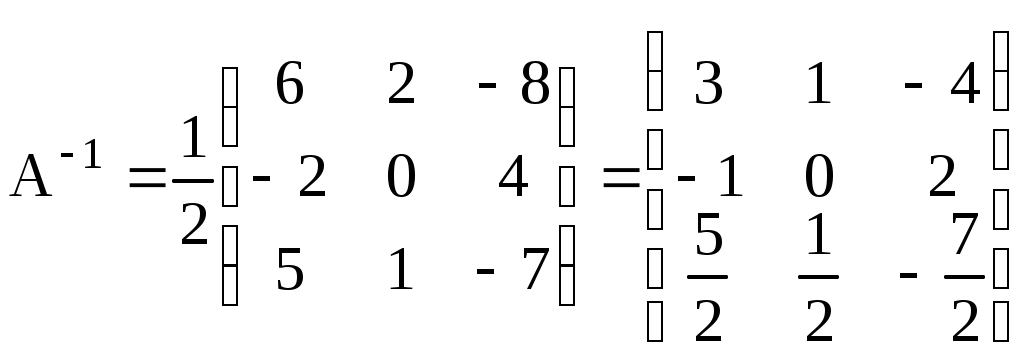




Найти: г) AA⁻¹;



Найти: д) A⁻¹A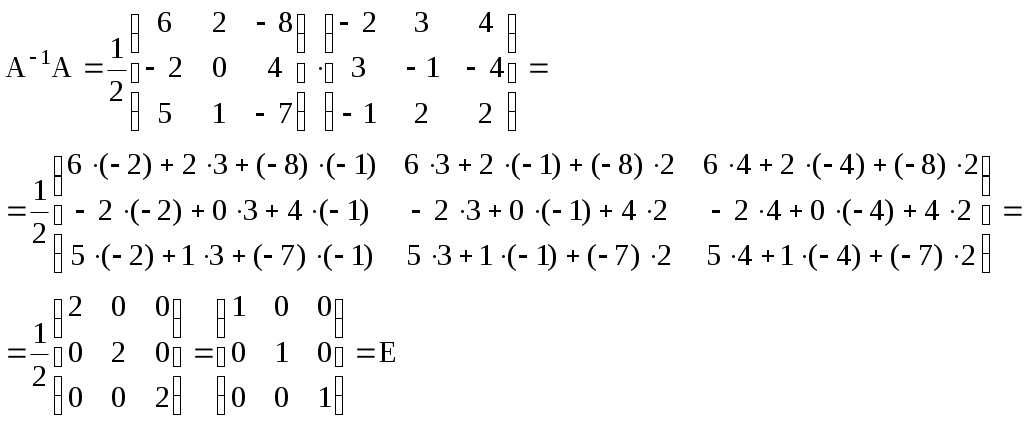



т.е. обратная матрица найдена верно.