Зинченко. 1. Предмет теории вероятности. Вероятность и статистика

• Название: 1. Предмет теории вероятности. Вероятность и статистика
• Анкор: Зинченко.docx
• Дата: 10.07.2018
• Размер: 224.21 Kb.
• Имя файла: Зинченко.docx
• Тип: Документы; #21298
• страница: 2 из 5

Моменты

Производящая функция моментов биномиального распределения имеет вид:

,

откуда, ,

а дисперсия случайной величины..

18. Нормальное распределение,

также называемое гауссовским распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр ? — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а ?? — дисперсия.Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, могущих вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

19. Вероятность попадания в заданный интервал нормальной случайной величины Как уже было установлено, вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.
Для нормально распределенной случайной величины соответственно получим:
. Преобразуем последнее выражение, введя новую переменную . Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.
Для замены переменной в определенном интеграле еще необходимо заменить дифференциал и пределы интегрирования, предварительно выразив переменную из формулы замены:
;;– нижний предел интегрирования;
– верхний предел интегрирования; (для нахождения пределов интегрирования по новой переменной в формулу замены переменной были подставлены и – пределы интегрирования по старой переменной ).
Подставим все в последнюю из формул для нахождения вероятности: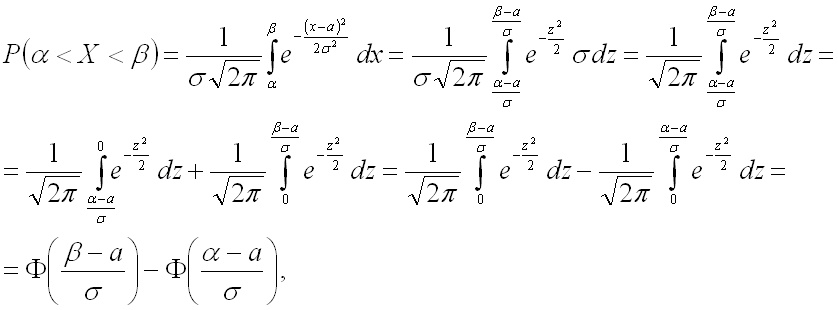
где – функция Лапласа.
Вывод: вероятность того, что нормально распределенная случайная величина примет значение, принадлежащее интервалу , равна:
,
где – математическое ожидание, – среднее квадратическое отклонение данной случайной величины.

20. Регрессио́нный (линейный) анализ 

— статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X₁,X₂,...,X_p. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Ложная корреляция), а не причинно-следственные отношения.