Курсова. Курсова робота. 1. Призначення та принип дії системи Функціональна схема сар та передавальні функції ланок
 Скачать 1.01 Mb. Скачать 1.01 Mb.
|
|
Зміст 1. Призначення та принип дії системи 2. Функціональна схема САР та передавальні функції ланок 3. Структурна схема САР та передавальні функції ланок. 4. Аналіз систем автоматичного регулювання 1) Дослідження стійкості системи САК по кореням характеристичного рівняння системи 2) Дослідження стійкості системи САК за критерієм Гурвіца 3) Дослідження стійкості системи САК за критерієм Гурвіца Михайлова 4) Дослідження стійкості системи САК за критерієм Найквіста 5. Забезпечення необхідної якості процесу керування. Синтез САР Висновок Список використаної літератури Вихідні данні:
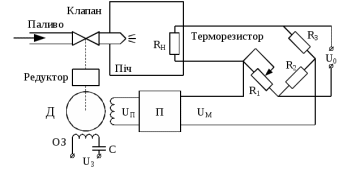 На схемі Ѳ– температура печі (регульована величина); ѲЗ– задане значення температури печі; ∆Θ=ΘЗ-Θ–відхилення температури; U0 – напруга живлення моста; UM – вихідна напруга моста; UK , U3 – напруги відповідно керування і збудження двигуна; µ – переміщення клапана; ʄ – збурення. Рівняння елементів системи: Об'єкт регулювання: 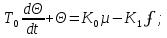 Міст: 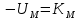 Δ Δ ; ;Підсилювач: 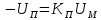 4 4Двигун з редуктором: 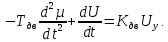 Характеристика роботи схеми Об’єкт регулювання представляє собою піч, у якій подане паливо спалюється й утворюється пропорційна масі палива кількість теплоти, що спричиняє підвищення температури в печі. Отримана теплота розсіюється у навколишнє середовище та йде на зміну структури та агрегатного стану речовин у печі. Усталений режим об’єкта регулювання характеризується рівністю кількості тепла, що утворюється в печі внаслідок згоряння палива, і розсіюваної у навколишнє середовище. Вхідною величиною є витрата палива, а вихідною – температура в печі. Електричний міст складається з резисторів R 2 , R З , змінного резистора R 1 і термометра опору (терморезистора). Термометр опору вимірює фактичну температуру в печі. За допомогою зміни опору резистора і задають бажану температуру в печі. Вхідна величина містка – температура в печі, а вихідна – напруга розбалансу. Напруга U п , що подається на якір двигуна постійного струму з незалежним збудженням. Залежно від полярності напруги U п вал двигуна переміщуватиме клапан в одну чи іншу сторону, збільшуючи або зменшуючи подачу палива. Вхідна величина двигуна з валом є підсилена напруга розбалансу, а вихідна – кут повороту валу. Редуктор представляє собою пристрій механічно зв’язаний з клапаном, який регулює подачу палива до об’єкту регулювання. Редуктор передає обертовий момент з валу електричного двигуна на клапан, таким чином регулюючи витрату палива, який подаються на об’єкт регулювання. Функіональна схема САК та передавальні функції ланок Зміна задаючої величини R1 призводить до появи напруги UМ , яка підсилюється підсилювачем до напруги UК , що подається на двигун, який через редуктор переміщує клапан так, щоб витрата палива змінювалась в таку сторону, щоб компенсувати зміну температури в печі. Збурюючою величиною може бути зміна температури навколишнього середовища, теплоємність оточуючого повітря (а значить атмосферного тиску і вологості) та ін. Отже, збурення призводить до порушення теплової рівнноваги й зміні температури в печі. Ця зміна температури приводить до зміни опору терморезистора й розбалансу мосту, який усувається шляхом, аналогічним до випадку зміни задаючої величини 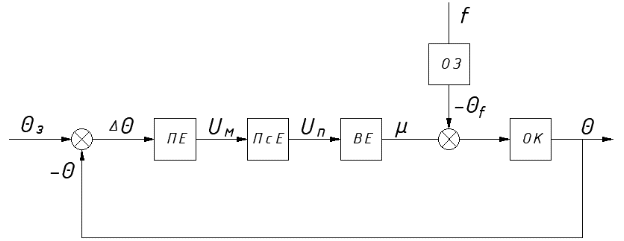 Функціональна схема системи автоматичного регулювання температури в печі. Елементи схеми: ПЕ - перетворювальний елемент; ПсЕ - підсилювальний елемент; ВЕ - виконуючий елемент; ОК – об’єкт керування; ОЗ – об’єкт збурення. Рівняння електричного моста має вигляд: 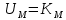 Δ Δ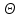 де Uм - вихідна величина, напруга на вимірювальній діагоналі моста; - вхідна величина, відхилення температури в печі від заданого значення Тоді рівняння (2.1) в операторній формі матиме вигляд: Uм(р)=kм*Θ(р) Передаточна функція моста: Wм(р)= 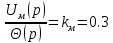  Рисунок 3. Структурна схема електричного моста. Рівняння підсилювача має вигляд: Un=knUm де Un - вихідна величина, Um – вхідна величина kn – коефіцієнт підсилення. В операторній формі рівняння (2.4) запишеться: Uk ( p ) = knUm ( p ) Передаточна функція підсилювача: Wn(p)=  =kn=22 =kn=22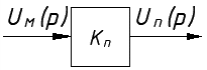 Рисунок 4. Структурна схема підсилювача. Рівняння, що описує роботу двигуна з редуктором: 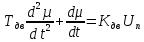 Де Un – вхідна величина. Операторна форма рівняння (2.7): ТдвР2 µ (р)+р* µ (р)=kдвUk(p) µ (p)(Tдвр2+р)=kдвUk(p) Передаточна функція двигуна з редуктором матиме вигляд: Wдв(р)= 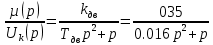 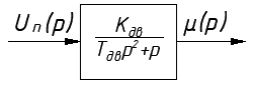 Рисунок 5. Структурна схема двигуна з редуктором. Рівняння об’єкта керування має вигляд: Т0 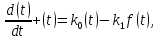 Де - вихідна величина; і f – регулююча і збурююча дії Знаємо, що вихідна величина має дві складові: = + f Тоді рівняння (2.10) розбивається на два рівняння, при =0 і f=0. В операторній формі вони матимуть вигляд : (Т0р+1)(р)=k0(p) (Т0р+1)(р)=k1f(p) Рівнянням (2.12) і (2.13) є передаточними функції об’єкта: 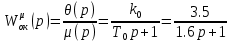 і за каналом збурення 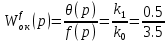 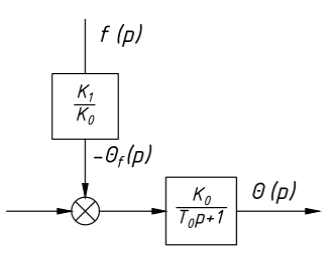 Структурна схема САК та передавальні функції системи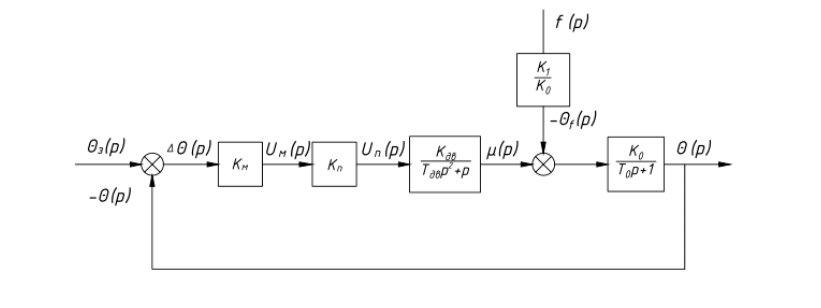  Для знаходження передавальних функцій системи за каналами задаючої і збурюючої дії користуються правилами еквівалентних перетворень структурних схем. Спочатку, знаходять передавальну функцію розімкнутої системи: 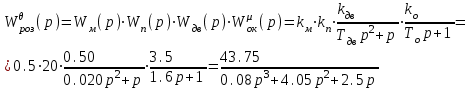 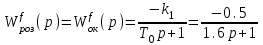 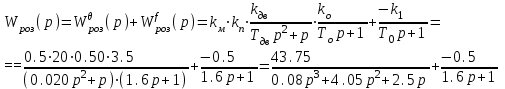 Передавальна функція замкнутої системи: 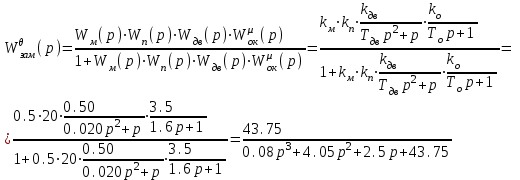 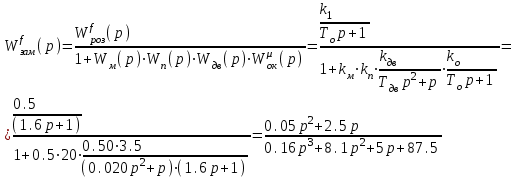 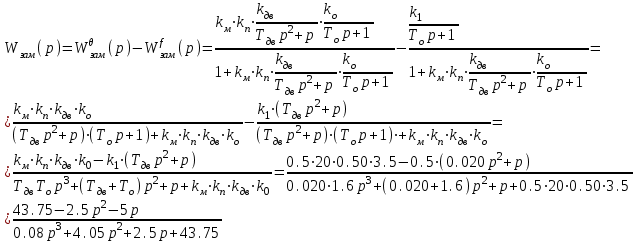 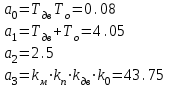 Аналіз системи автоматичного регулюванняА) Дослідження стійкості системи по кореню характеристичного рівняння системи Для того, щоб САР була стійкою необхідно і достатньо щоб всі корені характеристичного рівняння системи були лівій півплощині. Якщо серед коренів характеристичного рівняння системи є хоча б один, що знаходиться в правій півплощині, а інші - ліві, то САР є нестійкою. Передавальна функція замкнутої САР має вигляд: 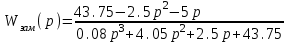 В програмному продукті MatLab, використовуючи функцію pole() отримаємо значення коренів характеристичного рівняння системи W=tf([-2.5 -5 43.75],[0.08 4.05 2.5 43.75]) pole(W) W = -2.5 s^2 - 5 s + 43.75 ----------------------------------- 0.08 s^3 + 4.05 s^2 + 2.5 s + 43.75 Continuous-time transfer function. ans = -50.2196 + 0.0000i -0.2027 + 3.2937i -0.2027 - 3.2937i 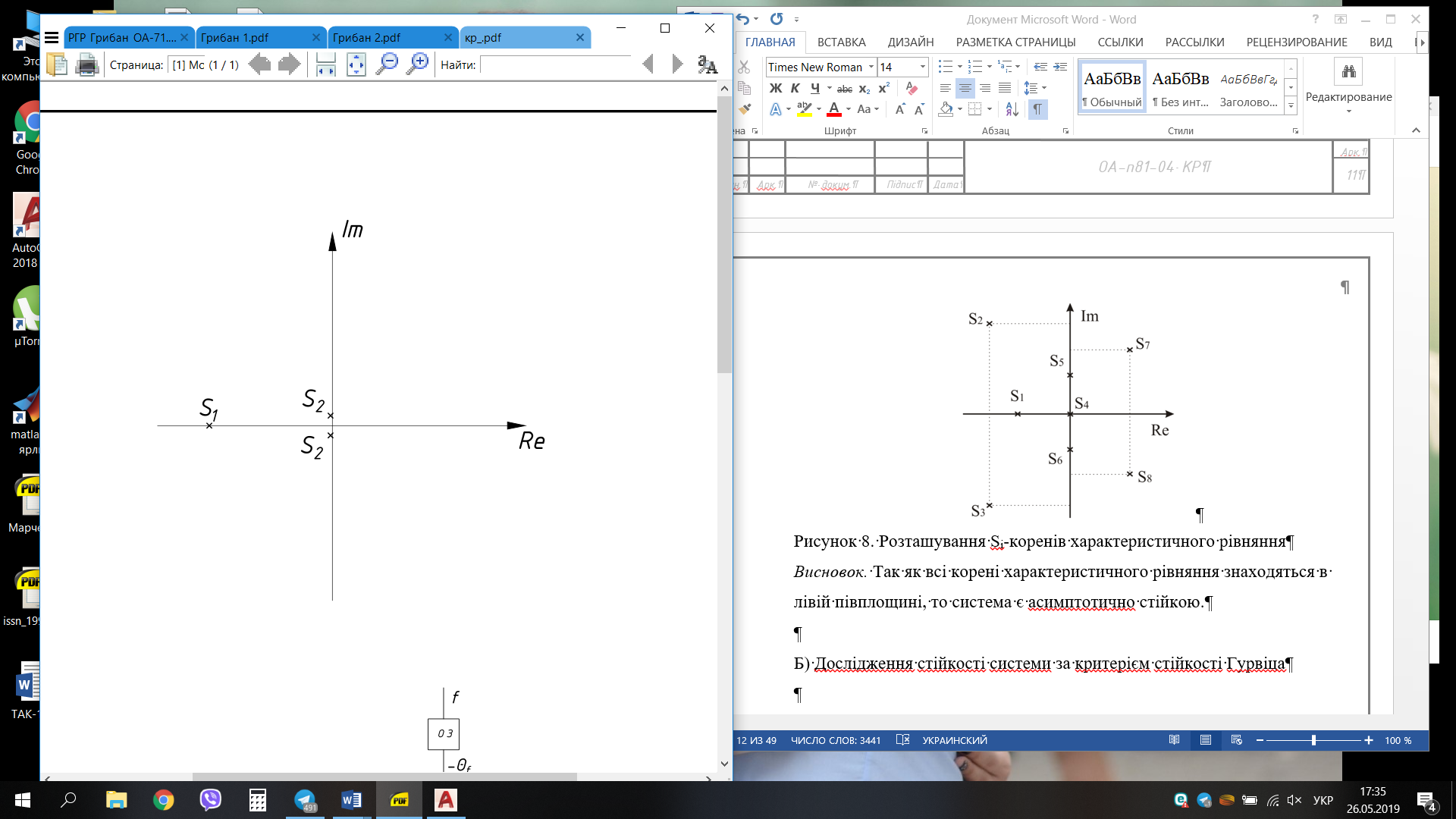 Рисунок 8. Розташування Si-коренів характеристичного рівняння Висновок. Так як всі корені характеристичного рівняння знаходяться в лівій півплощині, то система є асимптотично стійкою. Б) Дослідження стійкості системи за критерієм стійкості Гурвіца В основі критерія Гурвіца лежить характеристичне рівняння замкнутої системи. Критерій стійкості Гурвіца є алгебраїчним. Він формулюється так: якщо характеристичне рівняння системи має вигляд: 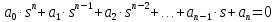 Система стійка, якщо всі коефіцієнти характеристичного рівняння додатні і визначник Гурвіца складений за певним правилом із коефіцієнті характеристичного рівняння, та діагональні мінори будуть > 0. Запишемо характеристичне рівняння замкнутої системи: 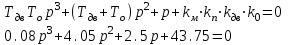 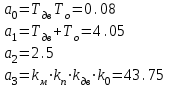 Складемо визначник Гурвіца для даного рівняння: 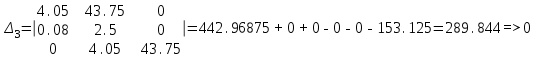 Діагональні мінори: 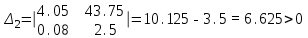 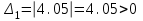 Головний визначник Гурвіца 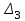 >0 і його мінори >0 і його мінори 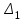 >0, >0, 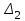 >0, тому система з даними параметрами стійка. >0, тому система з даними параметрами стійка.Визначення критичного значення коефіцієнта передачі регулятора. Для знаходження критичного значення коефіцієнта системи необхідно підставити в діагональний мінор 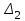 замість замість 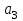 значення значення 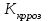 , при , при 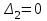 та отримати формулу для знаходження та отримати формулу для знаходження 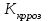 . . 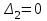 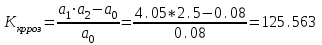 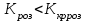 ; ; 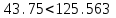 Отже, при 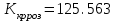 система стійка. система стійка.В) Дослідження стійкості системи за критерієм стійкості Михайлова Критерій стійкості оснований на аналізі характеристичного рівняння замкненої системи і зазвичай застосовується при порівнянні високих степенів диференціальних рівнянь. Критерій формується так: Замкнена система САК стійка, якщо годограф вектора Михайлова 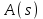 при зміні частоти від 0 до ꝏ починається при w=0 на дійсній піввісі і обходить в додатньому напрямку (проти годинникової стрілки) послідовно n квадрантів, ніде не перетворюється в 0, де n - степінь характеристичного рівняння замкнутої системи. при зміні частоти від 0 до ꝏ починається при w=0 на дійсній піввісі і обходить в додатньому напрямку (проти годинникової стрілки) послідовно n квадрантів, ніде не перетворюється в 0, де n - степінь характеристичного рівняння замкнутої системи. Запишем знаменник передавальної функції  замкнутої системи із рівняння : замкнутої системи із рівняння :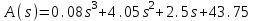 Зробимо заміну S=jw: 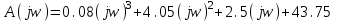 Розіб'ємо частотну характеристику на дійсну і уявну частини: 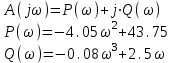 Прирівнюємо 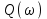 до 0 і знаходимо корені: до 0 і знаходимо корені: 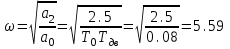 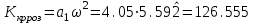 Використовуючи вбудовану функцію plot () в MatLab побудуємо годограф Михайлова і визначимо стійкість системи: >> w=0:0.01:10 >> p=-4.05*w.^2+43.75 >> q=-0.08*w.^3+2.5*w >> plot(p,q) >> grid 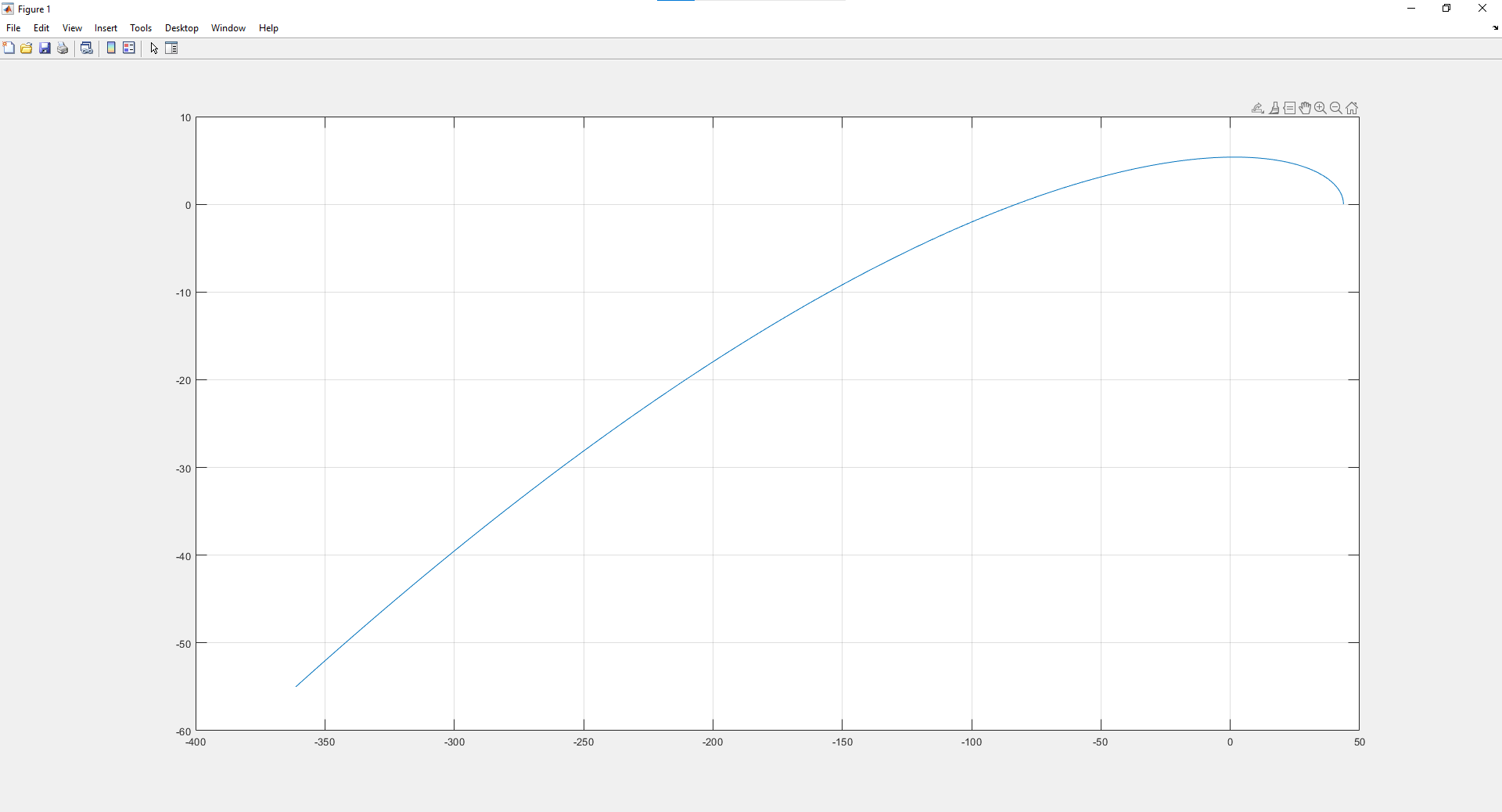 Рисунок 9. – Годограф Михайлова Виходячи з виду годографа Михайлова (рис. 9) видно, що система стійка, оскільки годограф починається на дійсній позитивної осі і проходить проти годинникової стрілки n-квадрантів, де n-порядок системи. В даному випадку n = 3. Г) Дослідження стійкості системи за критерієм стійкості Найквіста Пояснювальна частина. Цей критерій є частотним, і для оцінки стійкості САР необхідно скористатися передавальною функцією розімкнутої системи. Перейшовши в частотний діапазон (замінивши sj), необхідно побудувати годограф АФЧХ розімкнутої системи. Особливістю даного критерію є те, що по вигляду годографа АФЧХ розімкнутої системи оцінюється стійкість САР в замкнутому стані. Система автоматичного керування в розімкнутому стані може бути стійкою або нестійкою або нейтральною. Тому існує два підходи в оцінці стійкості системи. Система в розімкнутому стані є нестійкою або нейтральною. В даному випадку, в характеристичному рівнянні розімкнутої системи серед лівих коренів є хоча б один правий корінь або нульовий. Якщо система в розімкнутому стані є нестійкою або нейтрально, то для того, що б вона була стійкою і в замкнутому стані, необхідно і достатньо щоб годограф АФЧХ розімкнутої системи охоплював точку з координатами [–1; j0] в позитивному напрямку К/2 раз, де К – кількість правих чи лівих коренів. Годограф АФЧХ охоплює точку з координатами [–1; j0] в позитивному напрямку 0,5 рази, отже, система в замкнутому стані є стійкою. Передаточна функція замкнутої системи: 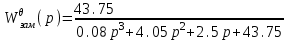 Використовуючи вбудовану функцію nyquist () в MatLab побудуємо годограф Найквіста і визначимо стійкість системи: W=tf([43.75],[0.08 4.05 2.5 43.75]) nyquist(W) 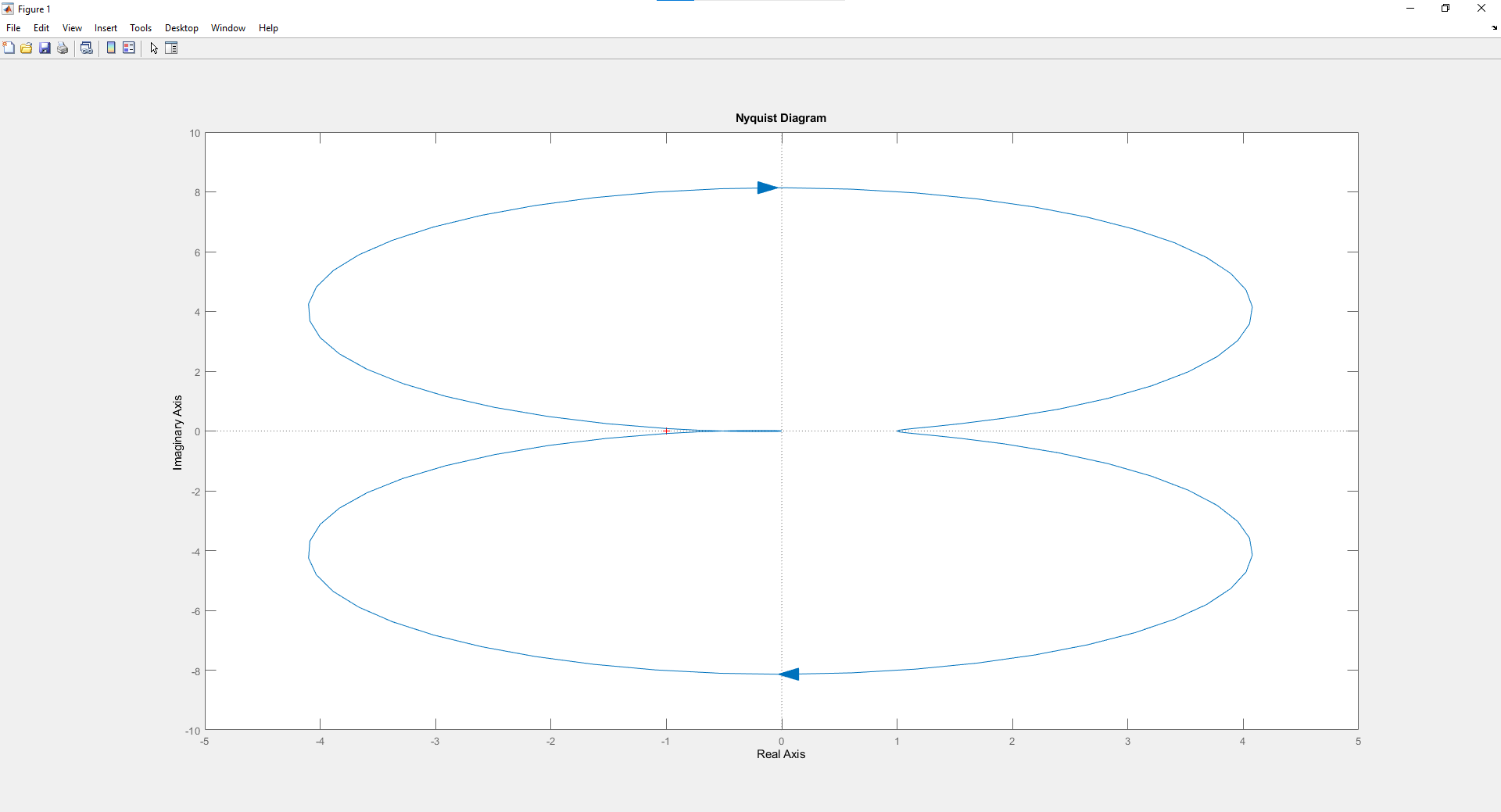 Забезпечення необхідної якості процесу керування. Синтез САРПроцес синтезу зазвичай включає в себе наступні операції: 1.Побудова реальної ЛАЧХ. Під реальною ЛАЧХ розуміється характеристика вихідної системи керування, яка побудована виходячи з вимог, що пред'являється до точності режимів стабілізації або стеження, до потужності на виході системи і т.п. Зазвичай під вихідною системою розуміється система, що складається з керованого об'єкта і керуючого пристрою і не забезпечена необхідними коригуючими пристроями, що забезпечували би необхідну якість перехідного процесу. 2. Побудова бажаної ЛАЧХ. Бажаною називають асимптотичну ЛАЧХ розімкнутої системи, що має бажані (необхідні) статичні і динамічні властивості. Бажана ЛАЧХ складається з трьох основних асимптот: низькочастотної, среднечастотної і високочастотної. Крім того, можуть бути спряжені асимптоти, які з'єднують основні. Параметри для побудови ЛАЧХ: Tдв = 0.020 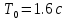 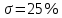 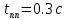 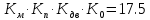 Знаходимо частоту зрізу по заданим параметрам: 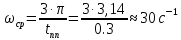 Знаходимо граничні частоти: 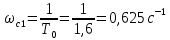 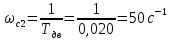 Будуємо бажану та асимптотичну ЛАЧХ за наступним алгоритмом: Під кутом (нахилом) –20 дБ/дек через точку 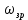 проводимо пряму до перетину із частотою проводимо пряму до перетину із частотою 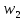 і і 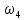 . Точки закінчення середньочастотної ділянки позначимо як a) і b) – точки перетину середньочастотної ділянки з високочастотною і низькочастотною відповідно. . Точки закінчення середньочастотної ділянки позначимо як a) і b) – точки перетину середньочастотної ділянки з високочастотною і низькочастотною відповідно.Спряжуємо (з’єднуємо) середньочастотну вітку ЛАЧХ з низькочастотною асимптотою з наклоном –40 дБ/дек. (точка с). Будуємо асимптотичну ЛАЧХ коригувального пристрою за формулою 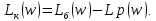 Вираховуємо постійні часи Т1, Т2, Т3, Т4. 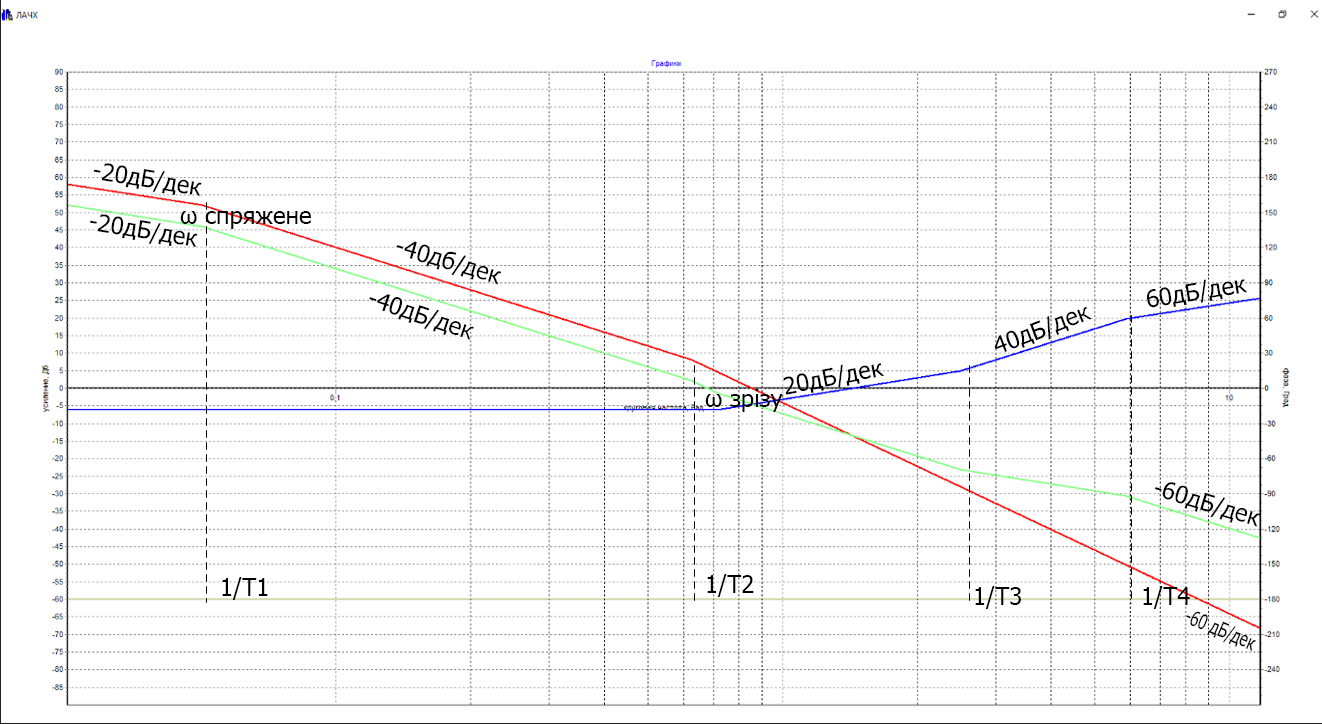 Бажана(червоний графік) та асимптотична(зелений графік) ЛАЧХ. Т1 = 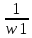 = 20 ; Т2= = 20 ; Т2= 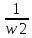 = 1.6; Т3 = = 1.6; Т3 = 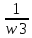 = 1.4; Т4 = = 1.4; Т4 = 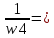 0.17; 0.17;Отже передавальна функція КП матиме вигляд: Таким чином, для корекції САК використовується двоінтегродифферинціючий послідовно корегуючій пристрій.В результаті корекції графік матиме вигляд показаний на рис. 13 Схема моделі в середовищі Matlab 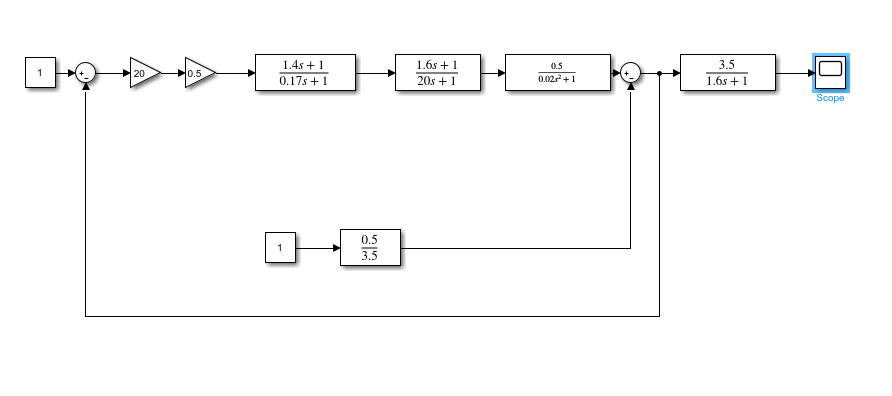 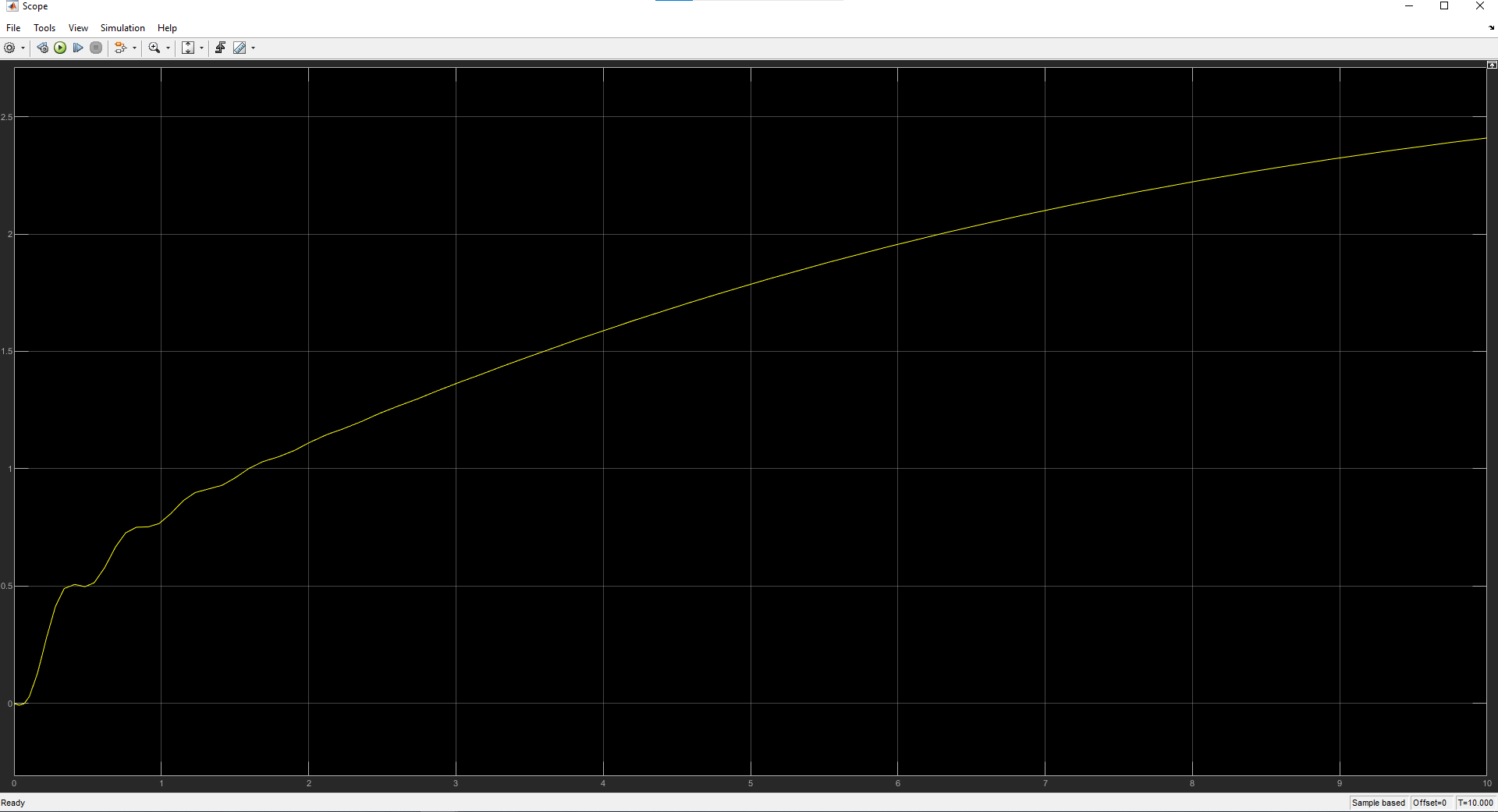 Графік перехідного процесу з кп 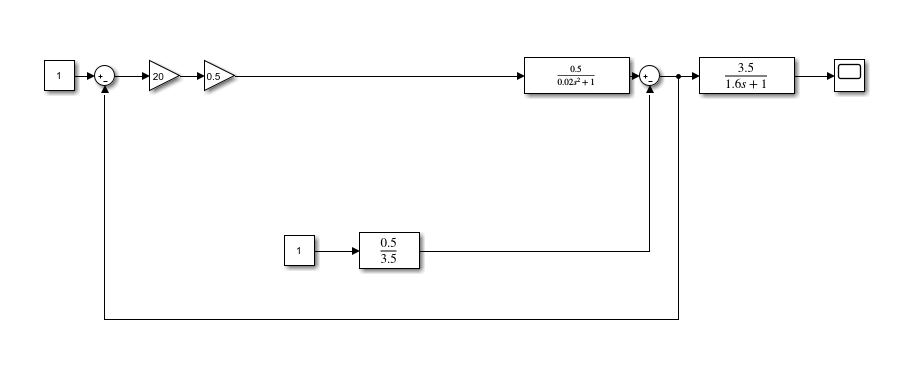 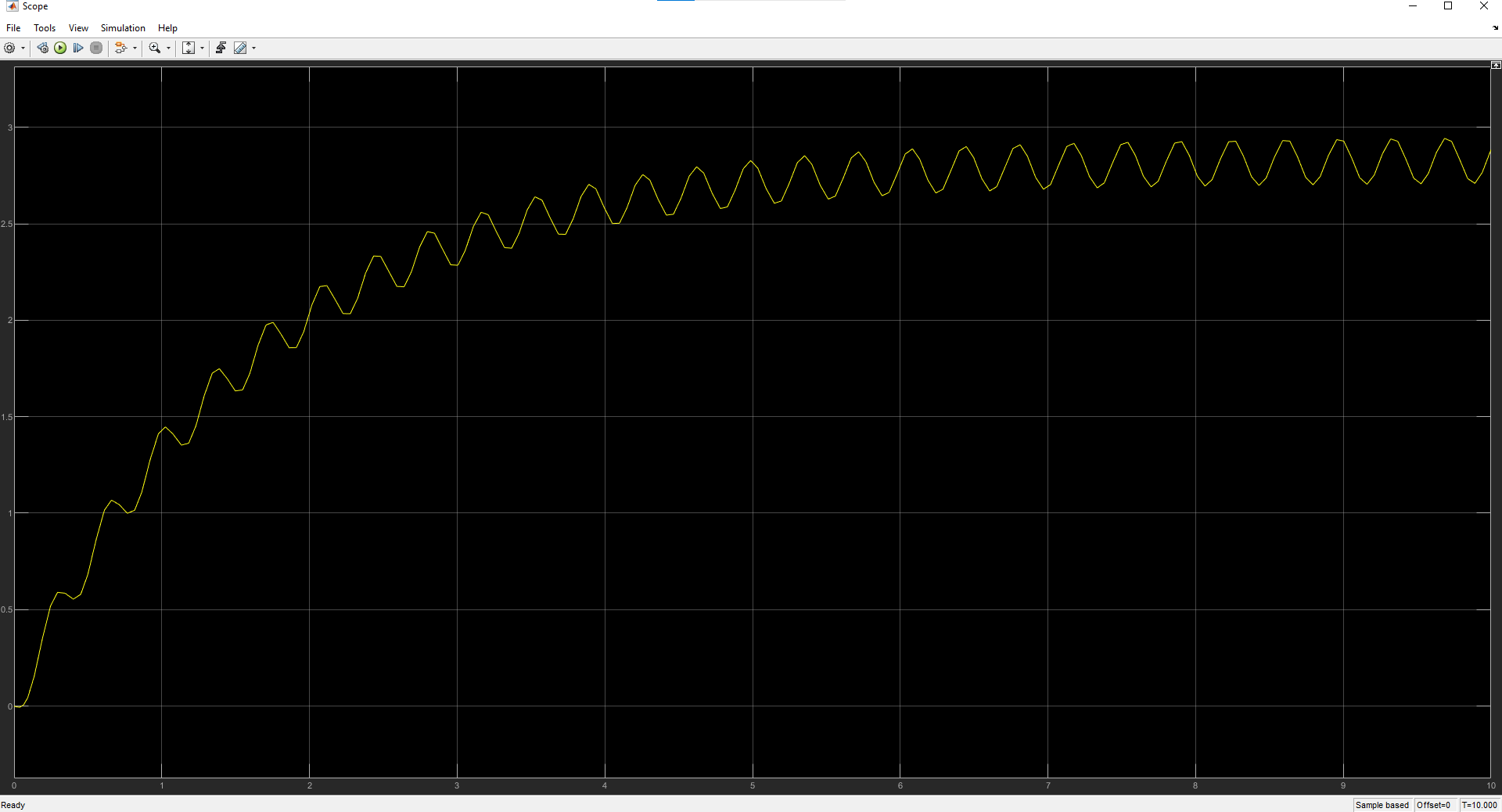 Графік перехідного процесу системи без КП Результати: По критеріям Гурвіца, Михайлова і Найквіста, система стійка. Після підключення до системи САР керуючого пристрою система стала більш стійкою, покращилися показники. Перерегулювання 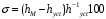 = 25% = 25%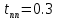 ВисновокВ курсовій роботі детально описав призначення і принцип дії САР згідно свого варіанту.Склав структурні схеми системи та визначив передавальні функції ланок. Знайшов передавальну функцію розімкнутої системи; передавальну функцію замкненої системи по задаючому впливу; передавальну функцію замкненої системи по збурюючому фактору; передавальну функціюзамкненої системи помилково регулювання. Провів аналіз систем автоматичного регулювання. Дослідження стійкості системи САК по кореням характеристичного рівняння системи; Дослідження стійкості системи САК за критерієм Гурвіца; Дослідження стійкості системи САК за критерієм Михайлова; Дослідження стійкості системи САК за критерієм Найквіста. Забезпечення необхідної якості процесу керування. Синтез САР. Здійснив набір схем САР в середовищі Matlab Simulink (скоригованої інескоригованої системи). Побудував криві перехідного процесу. Здійснити оцінкуякості перехідного процесу за результатами моделювання. СПИСОК ЛІТЕРАТУРИ 1. Лукас В.А. Теорія автоматического управления / В.А. Лукас. – М.: Недра, 1990. – 414с. 2. Иванов A.A. Теорія автоматического управления / А.А. Иванов. – М.: Недра, 1970. – 352 с. 3. Бесекерский В.А. Теория систем автоматического управления / В.А. Бесекерский, Е.П. Попов. – М.: "Профессия", 2004. – 747 с. 4. Власов К.П. Теория автоматического управления / К.П. Власов. – Харьков.: Изд-во "Гуманитарный центр", 2007. – 526 с. 5. Методы классической и современной теории автоматического управления : учебник в 5-и тт. Т.1: Математические модели, динамические характеристики и анализ систем автоматического управления / Под ред.. К.А. Пупкова, Н.Д. Егупова. – М.: Изд-во МГТУ, 2004. – 656 с. 6. Попович М.Г. Теорія автоматичного керування : підруч. для студ. вищ. техн. навч. закл. / М.Г.Попович, О.В. Ковальчук.– К. : Либідь, 2007.– 656 с. 7. Гоголюк П.Ф. Теорія автоматичного керування: Підручник / П.Ф. Гоголюк, Т.М. Гречин– Львів: Видавництво Національного університету "Львівська політехніка", 2008. – 285 с. 8. Милехин Л.Н. Основы теории управления. Учебно-методическое пособие / Л.Н. Милехин. – Казань: Академия управления «ТИСБИ», 2011 – 161 с. |
