1 производые и дифферинциалы

• Название: 1 производые и дифферинциалы
• Дата: 28.01.2021
• Размер: 206.98 Kb.
• Имя файла: Matesha_fizika.docx
• Тип: Документы; #172221
• страница: 1 из 4

1) ПРОИЗВОДЫЕ И ДИФФЕРИНЦИАЛЫ

Производной функции   в точке   называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.



Операция нахождения производной функции называется дифференцированием.

2) Применение методов дифференциального исчисления для анализа функций

Функция f (х) называется возрастающей в не­котором интервале, если для любых двух чисел х1 и х2 из этого интервала из неравенства х2 > х1 следует неравенство f (х2) > f(х1). Если же из неравенства х2 > х1 следует нестрогое неравен­ство f (х2)  f(х1), то функция называется неубывающей в этом интервале.

Функция f (х) называется убывающей в не­котором интервале, если для любых двух чисел х1 и х2 из этого интервала из неравенства х2 > х1 следует неравенство f (х2) < f(х1) .Если же из неравенства х2 > х1 следует нестрогое неравенство f (х2)  f(х1) , то функция называется невозрастающей в этом интервале. Функции возрастающие и убывающие, а также функ­ции невозрастающие и неубывающие называются монотонными.

Теорема. Если во всех точках некоторого интервала первая производная f'(х) > 0, то функция f (х) в этом интервале воз­растает. Если же во всех точках некоторого интервала первая производная f'(х) < 0, то функция в этом интервале убывает.

3) Производные сложных функций.

Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида

(f(g(x)))'=f'(g(x))⋅g'(x)

4) Правила интегрирования

Основные правила интегрирования

  

Постоянный множитель выносится за знак интеграла.

  

Интеграл от суммы равен сумме интегралов от слагаемых.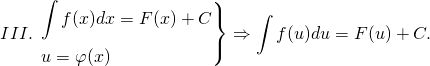

  

В частности,

  

где k и b — числа.

5) Вычисление неопределенных и определённых интегралов.

Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:

, 

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал,  C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.

Дифференциал-произвольное, бесконечно малое приращение переменной величины.

Свойства неопределённого интеграла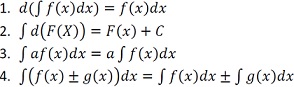



 

Определённый интеграл

Определенный интеграл- Приращение одной из первообразных функции f(x) на отрезке [a;b]. 

Общий вид определённого интеграла: 

где  f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал

Свойства определённого интеграла: см. св-ва определённого интеграла.

 Определённый интеграл вычисляется по формуле Ньютона –Лейбница:

6) Методы решения дифференциальных уравнений первого порядка с разделяющимися переменными.

Дифференциальное уравнение вида:f1(x)g1(y)dy=f2(x)g2(y)dxf1(x)g1(y)dy=f2(x)g2(y)dx

называют дифференциальным уравнением 1-го порядка с разделяющимися переменными. В данном разделе математики эти уравнения самые лёгкие в решении.

Для решения существует универсальный алгоритм: 

1. 
   Суть его состоит в том, чтобы обе части ду разделить на произведение функций, зависящих от разных переменных:f1(x)g2(y)f1(x)g2(y)
   
2. 
   Таким образом мы приводим исходное уравнение, заданное по условию, к виду:  g1(y)g2(y)dy=f2(x)f1(x)dxg1(y)g2(y)dy=f2(x)f1(x)dx
   
3. 
   Далее необходимо проинтегрировать обе части уравнения, из которых мы получим функцию y(x):∫g1(y)g2(y)dy=∫f2(x)f1(x)dx
   

7) Понятие о доказательной медицине.

Доказательная медицина подразумевает добросовестное, точное и осмысленное использование лучших результатов клинических исследований для выбора лечения конкретного больного.

8) Случайное событие.

Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления событияслужит оценкой его вероятности.

9) Определение вероятности (статистическое и классическое)

Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.

,

согласно классическому определению вероятность события А равна отношению числа исходов, благоприятствующих этому событию, к общему числу исходов, т.е.

,

10) Понятие о совместных и несовместных событиях, зависимых и независимых событиях.

несовместные события, если в условиях испытания каждый раз возможно появление только одного из них, т.е. никакие два не могут появиться вместе в этом испытании.

Случайные события называются совместными, если осуществление одного из них не исключает осуществления при этом других из перечисленных событий.

независимые события – вероятность события А не зависит от того, произошло ли событие В.

Если вероятность события А меняется в связи с появлением или непоявлением события В, то событие А называется зависимым от события В.

11) Теоремы сложения и умножения вероятностей.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместныхсобытий равна сумме вероятностей этих событий.

P(A+B)=P(A)+P(B).

Теорема об умножении вероятностей. Вероятность произведения независимых событий А и Ввычисляется по формуле:

P(A⋅B)=P(A)⋅P(B).

12) Непрерывные и дискретные случайные величины.

Дискретными случайными величинами называются такие, которые в результате испытаний могут принимать лишь отдельные, изолированные значения и не могут принимать значения промежуточные между ними.

Непрерывной случайной величинойназывается такая величина, которая в результате испытаний может принимать любые численные значения из непрерывного ряда их возможных значений в границах определенного интервала.

13) Распределение дискретных и непрерывных случайных величин, их характеристики: математическое ожидание, дисперсия, среднее квадратичное отклонение

Математи́ческое ожида́ние -среднее (взвешенное по вероятностям возможных значений) значение случайной величины.

Диспе́рсия случа́йной величины́ — мера разброса значений случайной величиныотносительно её математического ожидания

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)

14) Нормальный и экспоненциальный законы распределения непрерывных случайных величин.

Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности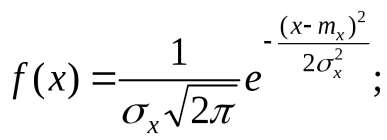



Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Плотность распределения величины XX(везде λ>0)λ>0):

f(x)={0, x<0λe−λx, x≥0f(x)={0, x<0λe−λx, x≥0

Функция распределения величины XX:

F(x)={0, x<01−e−λx, x≥0F(x)={0, x<01−e−λx, x≥0

Числовые характеристики можно найти по формулам:

M(X)=1λ,D(X)=1λ2,σ=1λ.

15) Функция распределения

Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть

F(x) = P(X < x).

16) Плотность вероятности

Плотность вероятности — один из способов задания распределения случайной величины

17) Стандартные интервалы.

Стандартный интервал а
Вероятность попадания в него случайной величины

b

Р(а  р (плотность) (Х) dx

Основы математической статистики.

Генеральная совокупность, выборка. варианта. статистика, оценка

18) Генеральная совокупность и выборка.

Генеральной совокупностью– называется совокупность объектов, произвольной природы, обладающих признаками доступными наблюдения и количественного измерения.

19) Объём выборки, репрезентативность

Число элементов выборки называется объемом выборки.

Репрезентативность — это степень соответствия характеристик выборки характеристикам генеральной совокупности.

20) Статистическое распределение (вариационный ряд). Гистограмма

Статистическое распределение– это совокупность вариант x_i и соответствующих им частот n_i.

Гистограмма частот – это ступенчатая фигура, состоящая из смежных прямоугольников, построенных га оной прямой, основания которых одинаковы и равны ширине класса, а высота равна или частоте попадания в интервал n_i или относительной частоте n_i/n. Ширину интервала i можно определить по формуле Стерджеса:

21) Характеристики положения (мода, медиана, выборочная средняя) и рассеяния (выборочная дисперсия и выборочное среднее квадратическое отклонение)

Мода (М_о) – это такое значение варианты, что предшествующее и следующее за ним значения имеют меньшие частоты встречаемости.

Медиана (М_е)-это значение признака. Относительно которого ряд распределения делится на 2 равные по объему части.

Выборочная средняя– это среднее арифметическое значение вариант статистического ряда



Выборочная дисперсия – среднее арифметическое квадратов отклонения вариант от их среднего значения: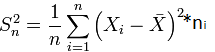



Среднее квадратическое отклонение – это квадратный корень из выборочной дисперсии:

S_в=√(S_в²)

22) Оценка параметров генеральной совокупности по характеристикам её выборки (точечная и интервальная).

Интервальная оценка

Интервальная оценка включает в себя два компонента:

Интервал в котором ожидается обнаружить оцениваемый параметр генеральной совокупности;

Вероятность обнаружения параметра в данном интервале.

Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке

23) Доверительный интервал и доверительная вероятность.

Доверительная вероятность α – некоторая заданная вероятность, с которой случ.величина попадает в определённый интервал.

Доверительный интервал в математической статистике - это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой что он содержит этот параметр с заданной вероятностью.

24) Сравнение средних значений двух нормально распределенных генеральных совокупностей.

Генеральные совокупности Х и Y распределены нормально, причем известны их дисперсии. Из этих генеральных совокупностей извлечены выборки объемов соответственно т и п, для которых найдены выборочные средние  и . При заданном уровне значимостиα проверяется нулевая гипотеза о равенстве математических ожиданий генеральных совокупностей:

Н_о: М (Х) = М (Y).

Статистическим критерием для проверки этой гипотезы является нормиро-ванная нормально распределенная случайная величина



25) Физические методы, как объективный метод исследования закономерностей в живой природе.

Всякое физическое исследование начинается с наблюдения, т.е. с изучения физических явлений в естественной, природной обстановке. Затем на основании размышлений и логических обобщений высказывается рабочая гипотеза – научное предположение, объясняющее эти явления. Гипотеза проверяется экспериментом, т.е. изучением явлений путем их воспроизведения в искусственных, лабораторных условиях. Гипотеза, подтвержденная экспериментом, становится научной теорией. Физическая теория представляет собой систему основных идей, обобщающих опытные данные и отражающих объективные закономерности природы. Физическая теория дает объяснение целой области явлений природы с единой точки зрения. Теория в дальнейшем подвергается неоднократной проверке практикой, которая вносит в теорию многочисленные дополнения и уточнения.

26) Значение физики для медицины.

В своей основе как физика, так и медицина — экспериментальные науки: все их законы и теории основываются и опираются на опытные данные. Если конкретный физический закон, справедливый для неживой природы, может быть верен и для живого организма, то этот факт можно использовать для целей медицинской физики.

Приготовление эмульсий.

Широко применяется ультразвук для приготовления однородных смесей (гомогенизация). Еще в 1927 году было обнаружено, что если две несмешивающиеся жидкости (например, масло и воду) слить в одну мензурку и подвергнуть облучению ультразвуком, то в мензурке образуется эмульсия, то есть мелкая взвесь масла в воде. Подобные эмульсии играют большую роль в промышленности: это лаки, краски, фармацевтические изделия, косметика.
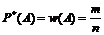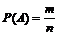