1. Проприаторное и открытое программное обеспечение (ПО). Лицензия по. Особенности проприаторного и открытого программного обеспечения, их достоинства и недостатки.
 Скачать 0.68 Mb. Скачать 0.68 Mb.
|
|
1.Проприаторное и открытое программное обеспечение (ПО). Лицензия ПО. Особенности проприаторного и открытого программного обеспечения, их достоинства и недостатки. Основные положения лицензионного соглашения проприаторного и открытого ПО. Примеры ОС и прикладных программ проприаторного и открытого ПО. Открытое программное обеспечение — программное обеспечение с открытым исходным кодом. Исходный код таких программ доступен для просмотра, изучения и изменения, что позволяет пользователю принять участие в доработке самой открытой программы, использовать код для создания новых программ и исправления в них ошибок. Проприета́рное программное обеспечение — программное обеспечение, являющееся частной собственностью авторов или правообладателей и не удовлетворяющее критериям свободного ПО (наличия открытого программного кода недостаточно). Правообладатель проприетарного ПО сохраняет за собой монополию на его использование, копирование и модификацию, полностью или в существенных моментах. Лице́нзия на програ́ммное обеспе́чение — это правовой инструмент, определяющий использование и распространение программного обеспечения, защищённого авторским правом. По сути, лицензия выступает гарантией того, что издатель ПО, которому принадлежат исключительные права на программу, не подаст в суд на того, кто ею пользуется. Преимущества и недостатки:
- происходит ожесточенная конкуренция - подгон вирусов на закрытые ПО 2. Программная поддержка: в закрытых быстрее решение ряда сложных задач (+), но они догоже (-), а в открытых медленне решение (-), но они дешевле (+). Основные положения лицензионного соглашения открытого ПО: 1. Любой пользователь может свободно использовать, копировать, изучать любой текст программы; 2. создавать новые закрытые версии; 3. все новые версии должны иметь корневое имя. Основные положения лицензионного соглашения проприаторного ПО: 1. Нельзя свободно копировать текст; 2. Нельзя просматривать, изучать код (текст); 3. Особые, специфические положения, касающиеся льгот. Примеры ОС открытого ПО: Linux OC(Mandriva 2007, 2010, 2011), Free BD OC. Примеры ОС проприаторного ПО: Linux XP, Linux Hat. Прикладные прог-мы открытого ПО: OpenOffice Pro на базе OpenOffice.org. Компоненты: Base, Impress, Math, Draw,Whiter; Прикладные прог-мы закрытого ПО: MS Office. Компоненты: Excell, Word, Power Point, Access, Out Look. 2.Перечислить и охарактеризовать основные события в разработке методов медицинской информатики в период времени 40-50 гг. и 50-70 годы 20-го века. Перечислить и охарактеризовать основные события в разработке методов медицинской информатики в периоды времени 70-80 г.г., 1995-2005 г.г. и с 2005-по н.вр. 1940-50 гг-создание основных теоретических и технических основ мед.информатики.Фон Нейман разработал аксиоматические основы формальных Методов Поддержки Принятия Решений (Проблемы принятия решений являются одними из самых важных проблем человеческой деятельности. Действительно, выбор лучшего варианта действий, способа научного использования ограниченных ресурсов, первоочередных задач является столь же существенным как для человека, начинающего свою жизнь, так и для умудренного опытом руководителя. Средством, помогающим человеку в сложных задачах выбора являются компьютерные системы поддержки принятия решений. Основным элементом таких систем являются методы принятия решений.) 1950-70 гг разработка базов.прикладных программ для компьютеров,обеспечивающих ППР в административной,лечебной деятольности. 70 гг-создание больших интегральных схем =компактное ЭВМ (нет персонала,развитие программ для рядовых пользователей) 1970-80 гг-создание единых программ технич систем для медицины,которые получили название госпитальной информационной системы Создание Электронных карт пациентов(системные электронные истории болезни) Создание действующих прототипов интеллектуальных Систем Принятия Решений в диагностике,лечении и лабораторных исследованиях (МСППР) 1980-94 гг Широкое распространение МППР для анализа и оптимизации решений мед проблем.Практическое установление самосоятельной ниши в развитии науки и клинич практики МИ. Установление самостоятел. Учебных программ и программ курсов МИ в США и стран ЕС. Рост практических знаний методов Байесовской диагностики и нейросетей. Широкое распространение методов машинного обучения и автоматизированных методов исследования в медицине и биологии.Разработка и распределение стандартных мед данными HL7(Health levels 7) ,стандарт протоколов обмена данными между локальными МИС. Развитиен МИС и оснащение ими больниц(преимущественно ППР) 1995-2005 гг-широкое распространение сетевых технологий обмена данными между локальными МИС. Переход МИС преимущественно задач клинической медицины(модуль административных решений в МИС-уровня прошлого века)то есть широекое распространение интеллектуальных МИС. Широкое распространение микрокомпьютерных устройств,работающих в режиме онлайн компьютерной сетью больницы Развитие методов биоинформатики,про «геном» Взрывное развитие глобальных сетевых ресурсов(Интернет) в обменах между МИС библиотеками,Интернет-базами данных в медицине. Появление региональных МИС,развитие телемедиа технология 2005г-разработка принципов национальной МИС и практический ввод в действие Развитие системы электронных карт пациентов Развитие и широкое распространение мобильных технологий Появление и развитие мед приложений Grid-технологий Примеры-запись и передача ЭКГ, уровень глюкозы в крови 3. Понятие о модели и моделировании. Дайте характеристику информационной модели. Дайте характеристику математической модели и методу математического моделирования. Назовите этапы процесса математического моделирования. Модель - упрощенное представление о реальном объекте, процессе или явлении. Модель - это, как правило, искусственно созданный объект в виде схемы, математических формул, физической конструкции, наборов данных и алгоритмов их обработки и т.п. Модель воспроизводит в специально оговоренном виде строение и свойства исследуемого объекта. Исследуемый объект, по отношению к которому изготавливается модель, называется оригиналом, образцом, прототипом. Модель - это объект, используемый вместо другого объекта с какой-то целью. Моделирование — это метод познания, состоящий в создании и исследовании моделей. Каждый объект имеет большое количество различных свойств. В процессе построения модели выделяются главные, наиболее существенные, свойства. Так, модель самолета должна иметь геометрическое подобие оригиналу, модель атома — правильно отражать физические взаимодействия, архитектурный макет города – ландшафт и т.д. Модель — это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса. Информационные модели нельзя потрогать или увидеть воочию, они не имеют материального воплощения, потому что они строятся только на информации. В основе этого метода моделирования лежит информационный подход к изучению окружающей действительности. Информационная модель – совокупность информации, характеризующая свойства и состояние объекта, процесса, явления, а также взаимосвязь с внешним миром. Математи́ческая моде́ль — это математическое представление реальности. Метод математического моделирования, основанный на построении и исследовании математических моделей различных объектов, процессов и явлений и получении информации о них из решения связанных с этими моделями математических задач, стал одним из основных способов исследования в так называемых точных науках. Технологическая цепочка вычислительного эксперимента включает в себя следующие этапы: · построение математической модели исследуемого объекта (сюда же относится и анализ модели, выяснение корректности поставленной математической задачи; · построение вычислительного алгоритма - метода приближенного решения поставленной задачи и его обоснование; · программирование алгоритма на ЭВМ и его тестирование; · проведение серии расчетов с варьированием определяющих параметров исходной задачи и алгоритма; · анализ полученных результатов; Каждый из этих этапов допускает возврат к любому из предыдущих с целью его уточнения и корректировки.Математическое моделирование — процесс построения и изучения математических моделей. 4. Назовите виды медицинских данных и приведите примеры. Назовите особенности медицинских данных. Как эти особенности учитываются в медицинской практике? Виды мед.данных: 1. длительные записи биопотенциалов (ЭКГ,ЭЭГ); 2. качественные данные (да или нет, «+» или «-»); 3. колличественные данные. Особенности медицинских данных (кол-ных): 1. точность (1/(Х-Хо), где Хо-истин. Знач-е) т. е. то, насколько среднее значение отличается от истинного; 2. необходимость правильной интерпретации (лежа, стоя); 3. ассоциативность. 5. Приведите примеры аналоговых сигналов, используемых для диагностики состояния пациента. Чем аналоговый сигнал отличается от цифрового? Дайте понятие дискретизации аналогового сигнала, времени и частоты дискретизации. Рекомендуемая для дискретизации ЭКГ частота. Какие устройства используются для преобразования аналогового сигнала в цифровой? Основное различие между аналоговыми и цифровыми сигналами заключается в самой структуре сигнального потока. Аналоговые сигналы представляют собой непрерывный поток, характеризующийся изменениями частоты и амплитуды. Это означает, что форма аналогового сигнала обычно похожа на синусоиду (т.е. гармоническую волну), представленную на рис. 1.2. Зачастую на иллюстрациях, изображающих гармоническую волну, весь сигнал характеризуется одним и тем же соотношением частоты и амплитуды, однако при графическом представлении сложной волны видно, что такое соотношение изменяется в зависимости от частоты. Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени. Эти значения называются отсчётами. Δt называется интервалом дискретизации. Частота дискретизации (или частота семплирования, англ. sample rate) — частота взятия отсчетов непрерывного во времени сигнала при его дискретизации (в частности, аналого-цифровым преобразователем). Измеряется в Герцах. Приборы: Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом, следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор. частота дискритизации /сохранения ЭКГ сигнала Гц 2000/250 6. Определите, что означает термин «порог нормальности» для количественного диагностического признака. Приведите пример, диагностического признака и его порога нормальности. Объясните значения терминов «истинно положительные» (TP), «истинно отрицательные» (TN), «ложно положительные» (FP) и «ложно отрицательные» (FN). Порог нормальности — это уровень, на котором данный (рассматриваемый нами) признак будет в норме. Примером диагностического признака может служить температура тела (порог нормальности 37.0), уровень фермента и т. д. TP (True Positives) – верно классифицированные положительные примеры (так называемые истинно положительные случаи); TN (True Negatives) – верно классифицированные отрицательные примеры (истинно отрицательные случаи); FN (False Negatives) – положительные примеры, классифицированные как отрицательные (ошибка I рода). Это так называемый "ложный пропуск" – когда интересующее нас событие ошибочно не обнаруживается (ложно отрицательные примеры); FP (False Positives) – отрицательные примеры, классифицированные как положительные (ошибка II рода); Это ложное обнаружение, т.к. при отсутствии события ошибочно выносится решение о его присутствии (ложно положительные случаи). 7. Дайте формулу для диагностической чувствительности диагностического признака (симптома) и пояснить статистическую значимость этой формулы. Чему равно максимальное значение чувствительности? При каком условии она его принимает? Приведите пример, когда целесообразно выбирать максимальное значение чувствительности. Se=TP/(TP+FN) диагностическая чувствительность показывает отношение числа здоровых людей к общему числу исследуемых. Диагностическая чувствительность — это доля позитивных результатов теста в группе (в популяции) больных пациентов. Максимальное значение чувствительности равно 1. она его принимает когда мало значение ложного отрицательного. 8. Дайте формулу для диагностической специфичности диагностического признака (симптома) и пояснить статистическую значимость этой формулы. Чему равно максимальное значение специфичности? При каком условии она его принимает? Приведите пример, когда целесообразно выбирать максимальное значение специфичности. Sp=TN/(TN+FP) диагностическая специфичность — это доля негативных результатов теста в группе здоровых пациентов. Максимальное значение специфичности равно 1. она его принимает когда мало значение ложного положительного. 9. Дайте формулу для прогностичности положительного результата (ППР) диагностического признака (симптома) и пояснить статистическую значимость этой формулы. Чему равно максимальное значение этой характеристики? При каком условии она его принимает?Прогностичность положительного результата ППР(PPV) P(D/S)=P(D*S)\P(S)=TP\TP+FP (отношение количесва исследуемых имеющих и симптои, и заболевание к общему количеству больных,имеющих симптом и исследуемых, имеющих симптом ,но не имеющих заболевание) 10. Дайте формулу для прогностичности отрицательного (ПОР) результата диагностического признака (симптома) и пояснить статистическую значимость этой формулы. Чему равно максимальное значение этой характеристики? При каком условии она его принимает? Прогностичность отрицательного результата ПОР(NPV) P(D’ S’/)=P(D‘*S’)\P(S)=TN\TN+FN (отношение количества исследуемых-здоровых,к общему количеству здоровых и имеющих заболевание без симптомов) 11. Как изменяется диагностическая чувствительность (Se) диагностического признака, если диагностическая специфичность (Sp) возрастает? Что предпочтительнее при диагностике инфаркта миокарда с помощью количественного диагностического признака (например, SGOT) установка «порога нормальности», при котором максимальна диагностическая чувствительность (Se) или диагностическая специфичность (Sp)? Почему? Приведите пример (примеры) когда желательно обратное соотношение (Se) или (Sp) и объясните его (их). Чувствительность (sensitivity): доля позитивных результатов теста в группе больных пациентов Чувствительность (Se) = TP/ TP+ FN Использование в клиническом обследовании Чувствительный тест часто дает положительный результат при наличии заболевания (обнаруживает его). Однако, особенно информативен он, когда дает отрицательный результат, т.к. редко пропускает пациентов с заболеванием. Специфичный тест редко дает положительный результат при отсутствии заболевания. Особенно информативен при положительном результате, подтверждая (предположенный) диагноз. Существует два мнемонических правила, значительно помогающих в использовании данных о чувствительности и специфичности диагностического теста. SnNout: мнемоническое правило, напоминающее о том, что признак, тест или симптом, имеющий высокую чувствительность (highSensitivity test), при отрицательном его результате исключает заболевание (Negative result rules out). SpPin: мнемоническое правило, напоминающее о том, что признак, тест или симптом, имеющий высокую специфичность (highSpecificity test), при положительном его результате подтверждает заболевание (Positive result rules in). Диагностические признаки и симптомы(S) Использование количественных данных для формальной диагностики. S,t,уровень холестерина,инфаркт миокарда,SGOT. Устанавливается предел(уровень)интервал нормальности. 
Если предел нормальности сдвинем вправо,то увеличится ложно отрицательное,уменьшиться ложно положительное.а нужно уменьш ложно отр.,поэтому лучше сдвигать влево.(в случае инфаркта) Операционные характеристики референтного теста.Статические х-ки диагностических знаков и симптомов. Диагностическая чувствительностьSe P(S\D)=P(D*S)\P(D)=TP\TP+FN Диагностическая специфичность Sp P(S’\D’)=P(D‘*S’)\P(D)=TN\TN+FP В идеальном случае FP=0 и FN=0, Se<100% и Sp<100% Чувствительность max,когда мало знач ложн. отр. специфичность max,когда мало знач ложн.полож.( max=1) и наоборот. Прогностичность положительного результата в задачах дифференциальной диагностики. 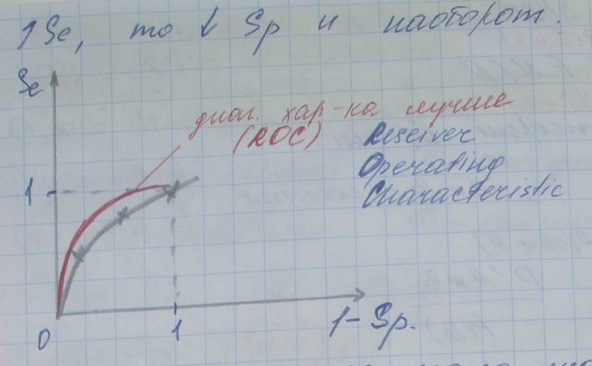 В медицинской практике если у теста высокая чувствительность, то по его отрицательному результату можно надежно исключить подозреваемую болезнь. При использовании такого теста мала вероятность пропустить больных. Ошибочно считать, что чувствительный тест хорош для включения болезни в дальнейшую диагностическую проработку, для выявления больных. Если у теста высокая специфичность, то его положительный результат (его почти никогда не бывает у здоровых!) дает основания включить подозреваемую болезнь в дальнейшую дифференциальную диагностику. | ||||||||||||||||
