РАСЧЕТ ОСТАТОЧНОЙ ПРОЧНОСТИ ЦИЛИНДРИЧЕСКОГО СОСУДА С ТРЕЩИНОЙ. МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ. 1. расчет остаточной прочности цилиндрического сосуда с трещиной цилиндрический сосуд диаметром 1,0 м имеет толщину стенки Н0,01 м и нагружен внутренним давлением р5 мпа
 Скачать 24.16 Kb. Скачать 24.16 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Институт сервиса и отраслевого управления Кафедра «Техносферная безопасность» ЭКЗАМЕНАЦИОННАЯ РАБОТА по дисциплине «Конструкционная безопасность»
Тюмень, 2020 1. РАСЧЕТ ОСТАТОЧНОЙ ПРОЧНОСТИ ЦИЛИНДРИЧЕСКОГО СОСУДА С ТРЕЩИНОЙ Цилиндрический сосуд диаметром 1,0 м имеет толщину стенки Н=0,01 м и нагружен внутренним давлением р=5 МПа. Материал сосуда – сталь с пределом текучести т 242 МПа и пределом прочности в 530 МПа.  с При испытании плоского образца шириной 2В=0,12 м с центральной трещиной длиной 2 =0,028 м были определены разрушающие напряжения 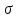 нетто 168МПа нетто 168МПаВ сосуде вдоль образующей обнаружен сквозной дефект 2 =0,019 м. Определить остаточную прочность сосуда. Для малопластичных материалов (в данном расчете материалом является стать) в определенном диапазоне температур, толщин и размеров величина КIc является постоянной и принимается в качестве основной расчетной характеристики. Критическое значение коэффициента интенсивности напряжений для разрушения по трещине нормального разрыва (КIc) определим по формуле (1.1) (глава 2 [1]):
где 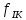 – функция, которая определяет поправку к решению для бесконечной пластины. Значение fIK для испытываемого образца, которое описывает значение для пластин ограниченных размеров с симметричной центральной трещиной [1], получилось равным 1,11. – функция, которая определяет поправку к решению для бесконечной пластины. Значение fIK для испытываемого образца, которое описывает значение для пластин ограниченных размеров с симметричной центральной трещиной [1], получилось равным 1,11.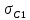 – номинальные разрушающие напряжения по брутто-сечению образца. После расчетов получили – номинальные разрушающие напряжения по брутто-сечению образца. После расчетов получили 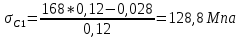 . .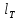 - равна начальной полудлине l плюс радиус пластической зоны у кончика трещины. Данное значение определяем по формуле Ирвина (глава 2 (17) [1]): - равна начальной полудлине l плюс радиус пластической зоны у кончика трещины. Данное значение определяем по формуле Ирвина (глава 2 (17) [1]): 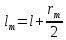 , где , где 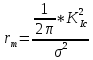 . .Подставив все значения и посчитав, получаем, что Критическое значение коэффициента интенсивности напряжений для разрушения по трещине нормального разрыва КIc = 30,01 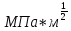 . .Вычисляя для проверки 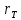 , обнаруживаем, что полученное значение , обнаруживаем, что полученное значение 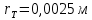 достаточно мало, что подтверждает предположение о характере разрушения. достаточно мало, что подтверждает предположение о характере разрушения.Критическое значение интенсивности напряжений для сосуда с трещиной подсчитаем также по формуле типа (1), однако учтем, что в случае замкнутого сосуда (цилиндр с днищами) напряженное состояние будет плоским и условную длину трещины lт будем определять соотношением 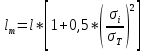 , где , где 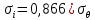 . .Подставив значения в формулу (1.1) и поняв, что уровень 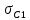 невысок, что позволяет нам предположить невысок, что позволяет нам предположить 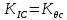 , найдем остаточную прочность сосуда с трещиной (давление рост.). , найдем остаточную прочность сосуда с трещиной (давление рост.).Решив полученное уравнение, получим: 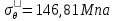 и и 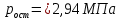 Предположение 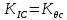 несколько завышает остаточную прочность. Подсчитаем рост., используя деформационный критерий критического раскрытия трещины в момент разрушения для образца и для сосуда по формуле (48) настоящего пособия [1]. Тем самым получаем: несколько завышает остаточную прочность. Подсчитаем рост., используя деформационный критерий критического раскрытия трещины в момент разрушения для образца и для сосуда по формуле (48) настоящего пособия [1]. Тем самым получаем: 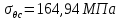 и и 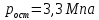 Остаточная прочность, подсчитанная по деформационному критерию, получилась больше остаточной прочности, рассчитанной из условия постоянства коэффициента интенсивности напряжений. Останавливаясь на деформационном критерии критического раскрытия трещины, получаем: 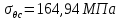 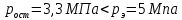 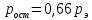 3. Предельное состояние строительных конструкций. СПИСОК ЛИТЕРАТУРЫ 1. Махутов Н. А., Пермяков В. Н. Механика деформирования и разрушения нефтегазохимических объектов: эл. учебное пособие – Тюмень: ТюмГНГУ, НТЦ НГП, 2012. – 176 с. |