Зачет. 1. Равные по условию и накрест лежащие при пересечении двух прямых секущей
 Скачать 109.49 Kb. Скачать 109.49 Kb.
|
|
∠ ∆ ⇒ Зачет №2. 1. Равные по условию 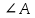 и и 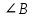 – накрест лежащие при пересечении двух прямых секущей – накрест лежащие при пересечении двух прямых секущей 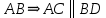 . .Углы при 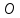 равны как вертикальные. равны как вертикальные. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. 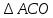 и и 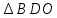 подобны по первому признаку подобия треугольников. подобны по первому признаку подобия треугольников. Из подобия следует отношение: 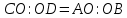 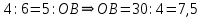 Коэффициент подобия равен отношению сходственных сторон. 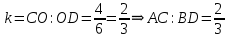 Отношение площадей подобных треугольников равно квадрату коэффициента их подобия: 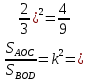 2. Сумма углов треугольника 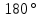 . .В 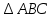 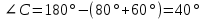 Найдем отношение длин сторон данных треугольников. 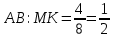 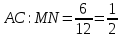 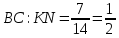 Стороны данных треугольников пропорциональны. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны. В подобных треугольниках против сходственных сторон лежат равные углы. 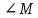 лежит против лежит против 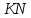 , сходственной , сходственной 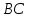 . . 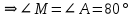 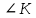 лежит против лежит против 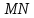 , сходственной , сходственной 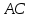 , , 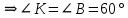 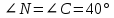 3. Так как прямая, пересекающая 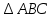 , проходит параллельно одной из сторон данной фигуры, то , проходит параллельно одной из сторон данной фигуры, то 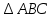 и и 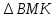 подобны. подобны. Из условия задачи видно, что сторона 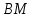 равняется 1 части, а сторона равняется 1 части, а сторона 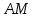 — 4 частям. Соответственно, сторона — 4 частям. Соответственно, сторона 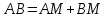 равна 5 частям. Таким образом мы выясняем, что стороны равна 5 частям. Таким образом мы выясняем, что стороны 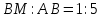 , а значит , а значит 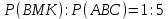 , где Р - периметр. , где Р - периметр.Далее вычисляем периметр 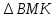 : принимаем периметр : принимаем периметр 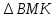 за за 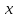 . .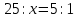 , ,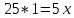 , ,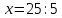 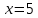 . .Периметр 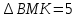 см. см.Зачет №3. 1. Средние линии треугольника находятся в том же отношении, что и стороны треугольника. Обозначим стороны треугольника буквами а, в и с. Тогда 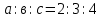 , т.е. , т.е. 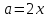 , , 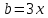 , , 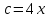 По условию, периметр 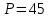 см, т.е. см, т.е. 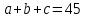 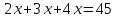 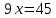 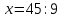 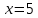 (см) (см)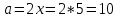 (см) (см)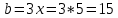 (см) (см)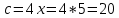 (см) (см)Ответ:10 см, 15 см, 20 см. 2. Медианы точкой пересечения делятся по длине в соотношении 2:1 считая от вершины. Рассмотрим 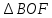 и и 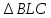 они подобны так как они подобны так как 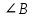 общий, общий, 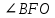 и и 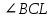 равны как углы при параллельных прямых. равны как углы при параллельных прямых. Медиана делит сторону треугольника на две равные части значит 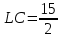 . . Составим уравнение 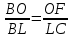 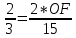 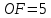 Аналогично для 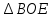 и и 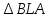 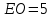 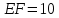 см см 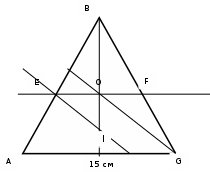 3. Найдём гипотенузу 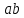 по теореме Пифагора: по теореме Пифагора: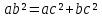 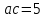 см см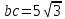 см см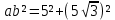 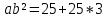 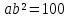 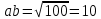 (см)- гипотенуза прямоугольного треугольника (см)- гипотенуза прямоугольного треугольника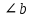 найдём через найдём через 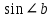 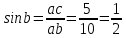 Отсюда 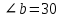 Ответ: 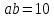 см; см; 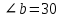 . .4. Для решения задачи воспользуемся теоремой синусов. Из нее следует, что: 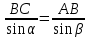 , то есть , то есть 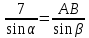 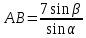 Теперь рассмотрим 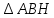 . По условию задачи . По условию задачи 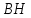 - высота, значит он является прямоугольным. - высота, значит он является прямоугольным. 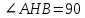 . .Тогда 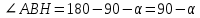 . .Для него будет верно соотношение: 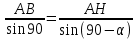 Из таблицы значений тригонометрических функций учтем что 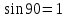 , тогда , тогда 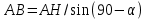 Из формул приведения тригонометрических функций учтем что 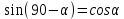 , тогда , тогда 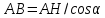 Подставим значение 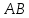 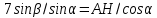 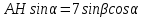 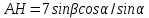 Из тех же тригонометрических тождеств выясним, что 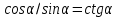 , тогда , тогда 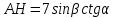 Ответ: 7sin β ctgα Зачет №4. 1. По свойству касательных, проведенных из одной точки: 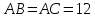 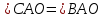 И по т. Пифагора: 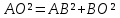 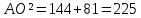 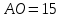 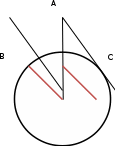 2. Окружность составляет 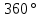 . .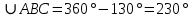 . .Пусть 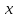 - коэффициент пропорциональности, тогда - коэффициент пропорциональности, тогда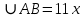 , , 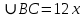 . .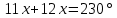 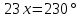 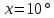 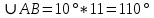 , а , а 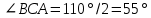 как вписанный, опирающийся на дугу как вписанный, опирающийся на дугу 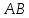 . .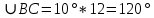 , а , а 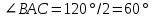 как вписанный, опирающийся на дугу как вписанный, опирающийся на дугу 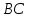 . .3. Даны две пересекающиеся хорды. Длины отрезков хорды 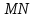 равны 12 и 3. Пусть длины каждого из отрезков второй хорды будут а, т.к. они по условию равны. равны 12 и 3. Пусть длины каждого из отрезков второй хорды будут а, т.к. они по условию равны.Углы с вершинами 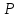 и и 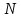 вписанные и опираются на одну и ту же дугу. Все вписанные углы, опирающиеся на одну и ту же дугу равны. вписанные и опираются на одну и ту же дугу. Все вписанные углы, опирающиеся на одну и ту же дугу равны. 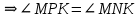 . .Соединим отрезками точки 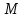 и и 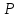 и точки и точки 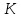 и и 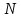 . .В 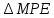 и и 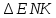 углы при углы при 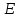 равны как вертикальные, равны как вертикальные, 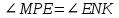 . ⇒ . ⇒ 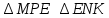 по первому признаку подобия треугольников. по первому признаку подобия треугольников.Из подобия следует отношение сходственных сторон: 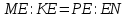 ⇒ ⇒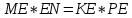 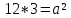 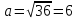 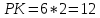 см см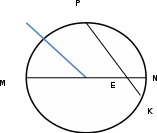 Зачет №5. 1. Рассмотрим равнобедренный 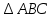 . Проведем высоту . Проведем высоту 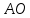 . Она является медианой. Следовательно . Она является медианой. Следовательно 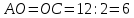 . .Рассмотрим прямоугольный 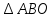 . По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов): . По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов):АВ2=АО2+ВО2; ВО2=АВ2-АО2; ВО2=100-36; ВО2=64; ВО=8. SАВС=1/2*ВО*АС; SАВС=1/2*8*12; SАВС=4*12; SАВС=48. Ответ: 48. 2. 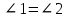 , так как , так как 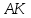 – биссектриса. – биссектриса.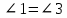 , так как , так как 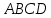 – параллелограмм. – параллелограмм.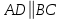 , , 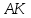 – секущая, – секущая, 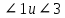 – накрест лежащие углы. – накрест лежащие углы.Тогда 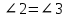 , следовательно , следовательно 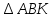 – равнобедренный (углы при основании равны). – равнобедренный (углы при основании равны).Получается, что 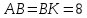 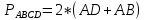 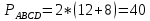 см смОтвет: 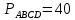 см. см. 3 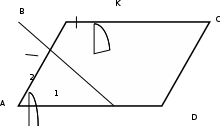 3. Проведем высоту трапеции 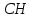 . А . А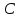 биссектриса прямого угла, значит биссектриса прямого угла, значит 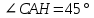 и и 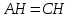 . . По Пифагору 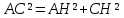 . . 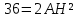 . . 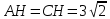 . . В прямоугольном 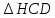 : : 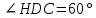 , значит , значит 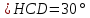 . Против угла 30° лежит катет, равный половине гипотенузы. . Против угла 30° лежит катет, равный половине гипотенузы. Тогда по Пифагору: 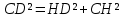 или или 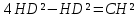 или или 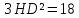 . .Тогда 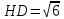 . Основание трапеции . Основание трапеции 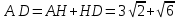 . .Итак, 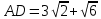 , , 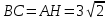 , , 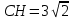 . .Площадь трапеции 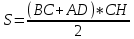 или или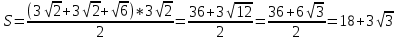 . .Ответ: 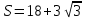 . .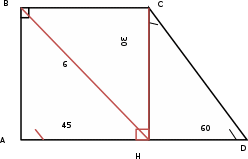 4. 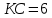 см, см, 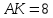 см. см. 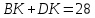 см. см.По свойству пересекающихся хорд: 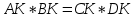 . .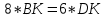 . . 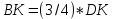 . .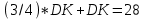 ⇒ ⇒ 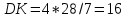 см. см.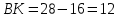 см. см.Ответ: 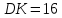 см, см, 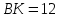 см. см.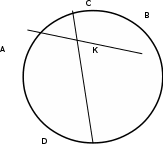 5. Радиус вписанной окружности в квадрат 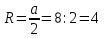 . .Радиус описанной окружности прямоугольного треугольника 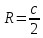 . .Значит гипотенуза прямоугольного треугольника 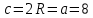 Катет против угла в 30° равен половине гипотенузы 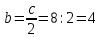 Другой катет 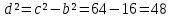 , , 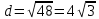 Площадь треугольника 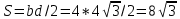 |
