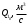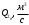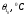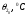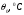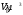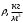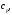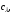математической моделирование. 1. Разработка математической модели объекта в виде дифференциальных уравнений и систем. 2
 Скачать 343.19 Kb. Скачать 343.19 Kb.
|
СодержаниеВВЕДЕНИЕ 2 1.Разработка математической модели объекта в виде дифференциальных уравнений и систем. 2 2. Получение передаточных функций по заданным динамическим каналам обьекта. 9 3. Получение математической модели объекта в виде переменных пространство состояний. 11 4. Получение дискретной математической модели объекта. 13 5 .Получение переходных функций объекта по передаточным функциям каналов. 17 6. Расчет коэффициентов передаточной функции по экспериментальной переходной функции методом площадей. Сравнение результатов расчета с истинной (аналитической) передаточной функцией объекта. 19 Заключение 23 Список использованной литературы 23 Графический материал 24 ВВЕДЕНИЕКачественные и количественные изменения в промышленности, науке и технике составляют основу для значительного повышения продуктивности труда и эффективности хозяйственной деятельности. Эти изменения возникают в результате осознанной, научно-обоснованной деятельности людей. Одним из направлений повышения продуктивности труда является использование современных математических методов и технических средств, таких, как планирование эксперимента, исследование операций, математическое моделирование и измерительная техника. Цели и методы моделирования направлены на повышение эффективности и производительности труда, повышение качества продукции, оптимизация планирования и управления, освобождение человека от работы во вредных условиях. В некотрых отраслях промышленности проектируемые системы являются особенно сложными. Возникают вопросы, которые недостаточно изучить теоретически. Это придает особое значение экспериментальным исследованиям. Часто для эффективного решения задач управления необходимо иметь адекватные технологическим процессам математические модели. Одним из направлений повышения производительности труда является использование математических методов и технических средств, таких как планирование эксперимента, исследование операций, математическое моделирование и вычислительная техника. Модель - это схема какого либо явления или физического объекта, заменитель оригинала. Моделирование объектов и систем управления является опосредованным отражением объектов и систем управления производственных процессов на основе замены реальных объектов и систем управления какими то другими, которые связаны с реальными и позволяют более простыми методами исследовать некоторые свойства исходных объектов и систем управления, а потом переносить полученные итоги исследования на реальные объекты и систем управления. Моделирование – это способ изучения объектов и систем управления, при котором эксперимент проводиться на его модели, а результаты качественно или количественно переносятся на оригинал. Моделирование базируется на подобии объектов. Подобными называются объекты, параметры которых в любой момент времени и в любой точке пространства определяются в определённое число раз. Один из объектов называется оригиналом, а второй его моделью. 1.Разработка математической модели объекта в виде дифференциальных уравнений и систем.ОБЪЕКТЫ РЕГУЛИРОВАНИЯ И ИХ ОСНОВНЫЕ СВОЙСТВА ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ ДЛЯ АНАЛИЗА ИХ СВОЙСТВ Объекты регулирования, с которыми приходится иметь дело при автоматизации химической промышленности, весьма разнообразны. Это могут быть отдельные аппараты, в которых выполняется какая-либо технологическая операция: теплообменник смешения, на выходе из которого поток вещества должен иметь постоянную температуру; напорный бак, в котором необходимо поддерживать постоянный уровень жидкости; химический реактор, в котором должен быть получен продукт заданного состава и т. д. Объектом регулирования может быть также отдельная часть сложного технологического аппарата. Примером подобного объекта может служить сборник ректификационной колонны, называемый обычно кубом, в котором необходимо поддерживать постоянный уровень высококипящего компонента смеси (кубового остатка). С другой стороны, объект может состоять из нескольких технологических аппаратов. В качестве примера можно привести цепочку последовательно работающих химических реакторов, на выходе которой необходимо поддерживать заданный состав продукта. Один и тот же аппарат с происходящим в нем технологическим процессом может быть объектом нескольких САР. Например, выпарной аппарат одновременно является объектом регулирования уровня упариваемого раствора, давления в аппарате и концентрации выходящего раствора. Как видно из приведенных примеров, объекты регулирования отличаются один от другого физико-химической природой протекающих в них технологических процессов, принципом действия, конструкцией и размерами применяемого технологического оборудования, режимом работы и многими другими факторами. Поэтому, если исследовать каждый объект отдельно, не сопоставляя его с другими уже исследованными объектами по наиболее существенным (для элементов САР) свойствам, то это значительно затруднило бы анализ САР и задержало развитие автоматизации производственных, процессов. Однако, несмотря на отмеченное разнообразие, многие, объекты, как элементы САР, обладают одинаковыми или достаточно близкими свойствами. Это позволяет классифицировать их по типам. Детальное изучение свойств типовых объектов значительно упрощает анализ конкретных промышленных объектов регулирования благодаря использованию метода подобия. В этом случае задача анализа сводится в основном к определению типа исследуемого объекта, свойства которого отождествляются со свойствами соответствующего типового объекта. Наиболее плодотворным методом описания свойств объектов регулирования (как и других элементов САР) является метод математического моделирования. Его суть заключается в том, что объект формально рассматривается как преобразователь поступающих на его вход сигналов в выходной сигнал. Математическая зависимость, связывающая выходной сигнал объекта с входным, называется математической моделью или характеристикой объекта регулирования. При математическом моделировании полностью абстрагируются от физической природы сигналов и самого процесса, происходящего в объекте. Поэтому одинаковые уравнения могут описывать поведение теплообменника, напорного бака или химического реактора при условии, что, как объекты регулирования, они обладают одинаковыми характеристиками. Переход от физического прототипа к математической модели дает ряд преимуществ. Во-первых,анализировать свойства модели проще и быстрее, особенно при использовании современных средств вычислительной техники, чем экспериментально определять поведение реального объекта регулирования при различных возможных режимах его работы в САР. Во-вторых, математическая модель иногда может быть составлена еще до создания реального объекта. В этих случаях результаты ее анализа могут быть использованы при проектировании для корректирования режима технологического процесса или конструкции оборудования объекта регулирования. В-третьих, анализ математических моделей позволяет выделить свойства объектов, наиболее существенные для процессов регулирования, и сгруппировать их по этим свойствам независимо от физической природы. Работа большинства объектов регулирования заключается в преобразовании по определенному закону материальных или энергетических потоков. При этом возможны два принципиально различных режима работы: статический и динамический. В статическом (установившемся) режиме приток вещества или энергии в объект равен стоку, так что объект находится в состоянии равновесия. Признаком статического режима работы является сохранение постоянного во времени значения выходного сигнала объекта 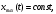 (1.1) (1.1)У многих промышленных объектов регулирования в статическом режиме каждому значению сигнала на входе соответствует определенное значение выходного сигнала 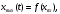 (1.2) (1.2)Такие объекты называются статическими, а приведенная выше зависимость, которая связывает значения выходного и параметров объекта в установившемся режиме, называется их статической характеристикой. Простейшем примером статического объекта регулирования может служить напорной бак (рис. 1.1). 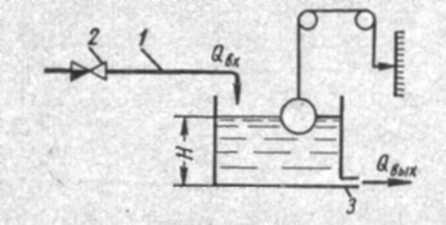 Рис 1.1.Напорный бак как объект регулирования уровня(где 1-входная труба,2-клапан,3-сливная труба) Жидкость поступает в него по трубе 1 через клапан 2и свободно вытекает по сливной трубе 3. Входным сигналом для этого объекта, очевидно, является изменение расхода Qвх жидкости через клапан 2,а выходным — изменение уровня Н. Если приток и сток равны, то количество находящейся в баке жидкости остается постоянным и ее уровень не изменяется. Это статический режим работы объекта, который описывается уравнением материального баланса: 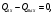 (1.3) (1.3)где 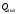 — расход жидкости через сливную трубу 3. — расход жидкости через сливную трубу 3.Известно, что расход жидкости при свободном истечении зависит от уровня и с достаточной точностью описывается уравнением 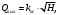 (1.4) (1.4)Где 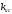 — коэффициент пропорциональности, который зависит от размеров и формы отверстия истечения. Подставим значение — коэффициент пропорциональности, который зависит от размеров и формы отверстия истечения. Подставим значение 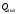 в (1.3) и после выполнения необходимых преобразований получим уравнение статической характеристики бака в виде в (1.3) и после выполнения необходимых преобразований получим уравнение статической характеристики бака в виде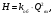 (1.5) (1.5)где 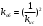 -коэффициент пропорциональности. -коэффициент пропорциональности.Это нелинейное уравнение и график статической характеристики такого объекта (рис. 1.2) также нелинеен. Если в состав САР входит хотя бы один нелинейный элемент, то такая САР также называется нелинейной. Анализ подобных систем чрезвычайно трудоемок, а во многих случаях он вообще невозможен. Поэтому всегда, когда это возможно, стремятся заменить нелинейную математическую модель линейной, которая, хотя и менее точна, но поддается анализу стандартными, хорошо разработанными и относительно простыми методами. Замена нелинейной математической модели более грубой линейной с целью упрощения анализа и синтеза САР называется линеаризацией модели[1]. 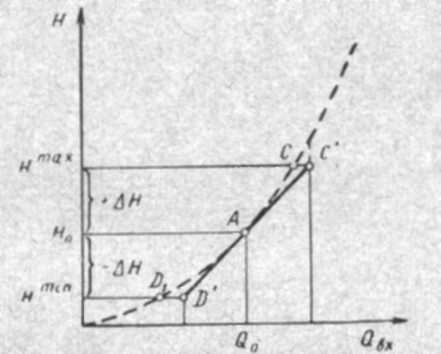 Рис 1.2.Статическая характеристика напорного бака. Наиболее простым является метод графической линеаризации, который применяется в тех случаях, когда статическая характеристика имеет вид плавной кривой. Линеаризация заключается в замене линейного участка характеристики в пределах возможного изменения входного и выходного параметров объекта прямой, касательной к статической характеристике в точке заданного режима работы. Рассмотрим применение этого метода на примере линеаризации характеристики напорного бака (рис. 1.2). Предположим, что в баке должно поддерживаться заданное значение уровня 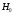 с точностью с точностью 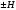 . Следовательно, рабочим участком статической характеристики служит криволинейный отрезок CAD,в середине которого находится рабочая точка А.Заменим его отрезком CAD'прямой, касательной к статической характеристике в рабочей точке, который и будет линеаризованной статической характеристикой данного объекта регулирования. Погрешность такой аппроксимации будет тем больше, чем больше отрезки ССи DD', которые зависят от кривизны истинной статической характеристики в окрестностях точки А и допустимого диапазона изменения регу-лируемого параметра (т. е. величины рабочего участка характеристики). . Следовательно, рабочим участком статической характеристики служит криволинейный отрезок CAD,в середине которого находится рабочая точка А.Заменим его отрезком CAD'прямой, касательной к статической характеристике в рабочей точке, который и будет линеаризованной статической характеристикой данного объекта регулирования. Погрешность такой аппроксимации будет тем больше, чем больше отрезки ССи DD', которые зависят от кривизны истинной статической характеристики в окрестностях точки А и допустимого диапазона изменения регу-лируемого параметра (т. е. величины рабочего участка характеристики).Следует отметить, что если в процессе работы САР регулируемый параметр по каким-либо причинам выйдет за пределы рабочего участка статической характеристики, принятые при линеаризации, то это может привести к существенному ухудшению качества регулирования. Математической основой данного метода линеаризации является разложение функции, описывающей статическую характеристику, в ряд Тейлора по малым приращениям входного сигнала 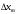 и ограничением ряда линейным членом. Проиллюстрируем возможности этого метода на том же примере напорного бака. и ограничением ряда линейным членом. Проиллюстрируем возможности этого метода на том же примере напорного бака.Разложение функции (1.5) в ряд Тейлора по малым приращениям параметра 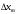 в окрестностях рабочей точки (т. е. при в окрестностях рабочей точки (т. е. при 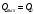 ) имеет вид ) имеет вид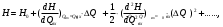 (1.6) (1.6)Пренебрегая членами ряда, в которые входит сомножитель 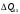 во второй и более высокой степени, и обозначая во второй и более высокой степени, и обозначая 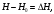 получим линеаризованное статической характеристики бака получим линеаризованное статической характеристики бака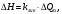 (1.7) (1.7)Где 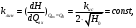 (1.8) (1.8)Графически это уравнение соответствует отрезку прямой CAD'па рис. 1.2. Кроме статических, существуют объекты регулирования, у которых при работе в статическом режиме отсутствует однозначная зависимость между входным и выходным сигналами. Такие объекты называются астатическими. Примером простейшего астатического объекта регулирования может служить бак, из которого жидкость откачивается насосом постоянной производительности (рис. 1.3). У такого объекта состояние равновесия возможно только в одном случае — когда приток жидкости в бак равен производительности насоса. Это состояние равновесия может наступить при любом значении выходного сигнала (уровня), следовательно, однозначной зависимости между Ни 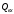 не существует. не существует.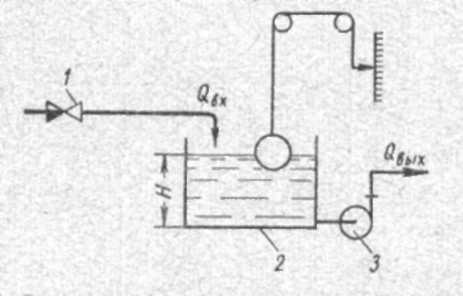 Рис 1.3.Астатический обьект регулирования(1-регулирующий клапан,2-бак,3-насос постоянной производительности) Статический режим работы, который рассматривался выше, не характерен для промышленных объектов регулирования. Гораздо чаще приходится иметь дело с динамическим режимом , который возникает всякий раз при нарушении равновесия между притоком и стоком вещества или энергии в объекте. В реальных условиях эксплуатации, когда на объект регулирования все время воздействуют различные возмущения, динамический режим является характерным режимом работы. Поэтому изучение динамических свойств объекта, т. е. определение его динамической характеристики, составляет главную задачу при анализе САР. Существуют два метода определения характеристик промышленных объектов регулирования. 1.Аналитический, когда на основании главных физико-химических закономерностей, определяющих ход технологического процесса в данном объекте, составляется уравнение математической модели объекта. Этот метод удобен тем, что при его использовании получаются уравнения, в которые входят основные параметры технологического процесса и применяемого оборудования. Поэтому наглядно видна связь этих параметров с характеристикой объекта и пути улучшения последней в случае необходимости. Математическую модель, полученную аналитическим методом, можно распространить на объекты с аналогичными технологическим процессом и конструкцией оборудования (с учетом их индивидуальных особенностей). Недостатки аналитического метода — его сложность и трудоемкость, из-за чего в широкой практике автоматизации он применяется сравнительно редко. Однако в последнее время интерес к этому методу увеличился в связи со все более широким распространением вычислительных машин, использование которых позволяет резко повысить производительность труда при выполнении расчетов. 2.Экспериментально-аналитический, когда статическая и динамическая характеристики объекта регулирования определяются путем механической обработки результатов экспериментов, поставленных на исследуемом объекте по определенной методике. Этот метод менее трудоемок, не требует детального изучения физико-химических закономерностей, определяющих работу объекта, не может быть осуществлен персоналом относительно невысокой квалификации. Полученные при этом результаты достаточно точны для большинства практических случаев, поэтому экспериментально-аналитический метод широко используется на практике. Его недостаток заключается в том, что математическая модель, полученная экспериментально, справедлива только для обследованного объекта и не может быть использована при изучении других объектов, даже близких к нему по технологии и аппаратурному оформлению[3]. АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ОБЪЕКТОВ РЕГУЛИРОВАНИЯ При использовании аналитического метода определения характеристик объектов регулирования за основу берут уравнения материального и энергетического баланса объекта. Если необходимо определить статическую характеристику, то уравнение баланса составляют для статического (установившегося) режима работы объекта. Типичным примером является вывод уравнения статической характеристики напорного бака (пункт 1) на основе уравнения его материального баланса. При определении аналитическим методом динамической характеристики объекта регулирования также составляют уравнения баланса, но для динамического (неустановившегося) режима работы объекта. Эти уравнения выражают связь скорости изменения регулируемого параметра с величиной материального или энергетического разбаланса, когорый является причиной возникновения динамического режима работы объекта. Рассмотрим применение аналитического метода на примере 1 [3]. Пример 1. Определить характеристики теплообменника смешения (рис. 1.4) как объекта регулирования температуры.Теплообменник является смесителем непрерывного действия, в который поступают два потока одинаковой по физическим свойствам жидкости (т. е. с одинаковой теплоемкостью 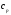 иплотностью иплотностью 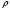 ). ).Первый поток имеет постоянный расход. 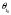 ипеременную температуру ипеременную температуру 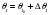 .Второй поток жидкости имеет постоянную температуру .Второй поток жидкости имеет постоянную температуру 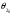 , а расход его , а расход его 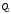 поддерживается на таком уровне, чтобы температура поддерживается на таком уровне, чтобы температура 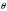 жидкости, выходящей из смесителя, была равна постоянной заданной величине жидкости, выходящей из смесителя, была равна постоянной заданной величине 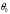 . Следовательно, для данного объекта возмущающим воздействием служит изменение температуры . Следовательно, для данного объекта возмущающим воздействием служит изменение температуры 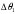 первого потока, регулирующим воздействием является изменение расхода первого потока, регулирующим воздействием является изменение расхода 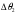 второго потока , а регулируемым параметром-отклонение температуры второго потока , а регулируемым параметром-отклонение температуры 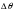 выходящего потока от заданного значения. выходящего потока от заданного значения.Чтобы упростить вывод уравнения статической и динамической характеристики, примем следующие допущения:cмеситель снабжен теплоизоляцией, так чтобы тепловыми потерями в окружающую среду можно было пренебречь; температура жидкости во всем объеме смесителя одинакова( смеситель идеального перемешивания) и равна температуре выходящего потока; расход 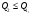 (1.9) (1.9)Для определения статической характеристикисоставим уравнение теплового баланса смесителя в установившемся режиме Таблица1.1
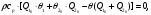 (1.10) (1.10)Откуда с учетом условия (1.9) получим линеаризованное уравнение статической характеристики в виде. 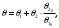 (1.11) (1.11)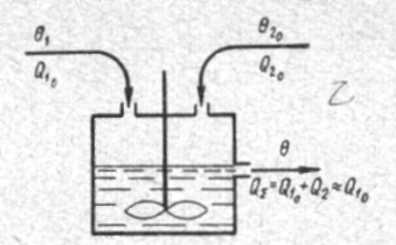 Рис 1.4.Теплоабменник смешения как объект регулирования температуры. При нарушении равновесия между притоком и стоком тепла в смеситель за малый промежуток времени 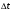 поступает некоторое дополнительное количество тепла поступает некоторое дополнительное количество тепла 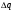 . В результате изменяется температура жидкости в смесителе и температура выходящего потока на величину . В результате изменяется температура жидкости в смесителе и температура выходящего потока на величину 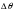 . Величина теплового разбаланса определяется зависимостью . Величина теплового разбаланса определяется зависимостью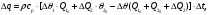 Где 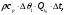 — дополнительное количество тепла, внесенное — дополнительное количество тепла, внесенноев смеситель первым потоком при изменении его температуры на 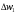 ; ; 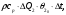 — дополнительное количество тепла, внесенное в смеситель вторым потоком при изменении его расхода на — дополнительное количество тепла, внесенное в смеситель вторым потоком при изменении его расхода на 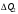 ; ;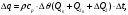 — дополнительное количество тепла, вынесенное — дополнительное количество тепла, вынесенноеиз смесителя выходящим потоком при изменении температуры жидкости в смесителе на величину 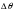 . .Учитывая условие (1.9), выражение для 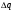 можно упростить: можно упростить: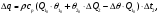 (1.12) (1.12)Изменение температуры жидкости в смесителе, вызванное разбалансом 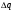 , равно , равно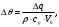 (1.13) (1.13)где V0 — рабочий объем смесителя (V0 = const). Подставим значение 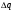 из (1.11) в (1.12) и после очевидных преобразований, переходя к пределу при из (1.11) в (1.12) и после очевидных преобразований, переходя к пределу при 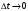 , получим уравнение, описывающее динамическую характеристику данного объекта: , получим уравнение, описывающее динамическую характеристику данного объекта: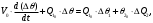 (1.14) (1.14)Выведенное ранее уравнение статической характеристики (1.13) может быть получено из (1.13) при выполнения условия равновесия, т.е когда 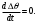 Для приведения уравнения (1.14) к безразмерной форме введем следующее обозначение: Для приведения уравнения (1.14) к безразмерной форме введем следующее обозначение: 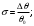 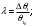 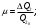 Подставляя данные из таблицы 1.1 получим следующее: 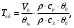 (1.15) (1.15)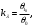 (1.16) (1.16)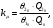 (1.17) (1.17)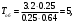 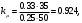 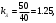 После подстановки их в уравнение (1.14) и проведения необходимых преобразований получим в оканчательном виде. 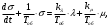 (1.18) (1.18)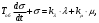 (1.19) (1.19)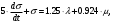 (1.20) (1.20)Преобразуем в область Лапласа 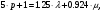 (1.21) (1.21)2. Получение передаточных функций по заданным динамическим каналам обьекта.Передаточные функции характеризуют изменение сигнала при прохождении через систему. Отношение Лапласовых изображений выходной и входной величин системы при нулевых начальных условиях называется передаточной функцией системы W(p) 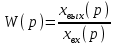 (2.1) (2.1)где xвх(p) иxвых(p) – изображение по Лапласу входной и выходной величин системы. По передаточной функции системы W(p) и изображению ее входной величины можно найти изображение выходной величины 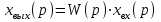 (2.2) (2.2)При наличии одной входной и одной выходной величины система или звено имеют только один канал прохождения сигнала, а следовательно, и одну передаточную функцию. Если же система или звено имеют несколько каналов прохождения сигнала, что возможно при нескольких выходных и входных величинах, то прохождение сигнала в каждом канале характеризуется своей передаточной функцией[2]. Передаточные функции теплообменника могут быть найдены по его уравнению динамики, а также по структурной схеме (рис.2.1), составленной по равенствам (1.19). 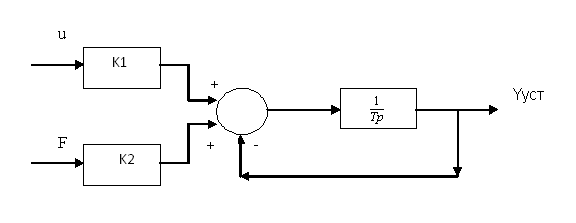 Рисунок 2.1-Структурная схема теплообменника смешения. Приведем без вывода передаточные функции теплообменника: 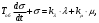 (2.3) (2.3)по каналу 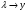 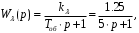 (2.4) (2.4)по каналу 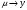 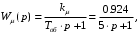 (2.5) (2.5)3. Получение математической модели объекта в виде переменных пространство состояний.Одной из распространенных форм математического описания линейных динамических систем являются уравнения следующего вида: 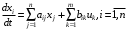 ; ;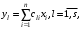 (3.1) (3.1)которые называют описанием в пространстве состояний. Это название связано с тем, что при uk = 0 достаточно задать начальное значение переменных xi, чтобы однозначно определить состояние системы xi(t), y1 для любого момента времени. Модель (3.1) содержит n дифференциальных уравнений 1-го порядка с k управляющими входными воздействиями, а также s алгебраических соотношений для связи выходных переменных системы y с переменными состояния x. Коэффициенты aij, bik, cli называют параметрами модели. Уравнения (3.1) удобно представить в матричной форме 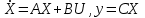 (3.2) (3.2)где X вектор переменных состояния; U − вектор управляющих (входных) воздействий; Y вектор выходов; A, B, C − матрицы параметров [2]. Модель (3.2), в сравнении с ранее рассмотренными моделями, формирует дополнительно n переменных внутреннего состояния системы, что увеличивает количество информации об объекте управления. Если модель системы управления задана с помощью одного дифференциального уравнения, которое в операторной записи имеет вид (d)y(t) = (D)u(t) (3.3) где (D) = Dn + n1Dn1 + …+ 0; (d) = mDm + m1Dm1 + … + 0, и m < n, то решение y(t) уравнения (3.3) совпадает с решением уравнения (3.2), имеющим следующие матрицы параметров: 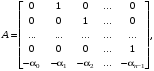 (3.4) (3.4)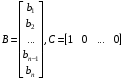 . (3.5) . (3.5)Элементы матрицы B находят из системы уравнений 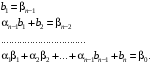 (3.6) (3.6)При этом начальные условия согласуют следующим образом: 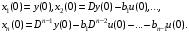 (3.7) (3.7)Структурная схема объекта с учетом полученных передаточных функций: 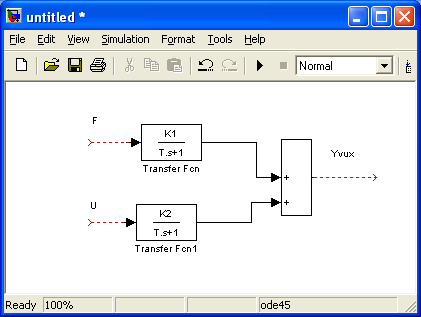 Рисунок 3.1-Структурная схема объекта Тогда вектор переменных состояния объекта в отклонениях от желаемых базовых значений примет вид: 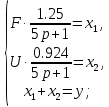 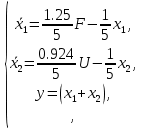 На основе полученных дифференциальных уравнений запишем матрицы А, B и S. 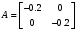 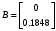 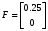 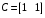 4. Получение дискретной математической модели объекта.Термин “дискретный” еще не сложился. Каждая система управления, в которой присутствует хотя бы один элемент, который не подчиняется непрерывному характеру изменения сигнала, может быть отнесен к классу дискретных систем. Для этих систем характерным является исчезновения сигнала информации хотя бы на небольшом интервале времени. Если эти интервалы устремить к нулю, то можно рассматривать систему как непрерывную. Дискретные системы более общие. В производстве часто технологические процессы непрерывные [2]. Пусть имеется на входе в дискретный элемент какой-то непрерывный сигнал. Введем период квантования. Заменяем реальное время на кванты т=к*Т к=0,1,…, 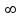 . Если Т . Если Т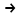 0 тогда имеем непрерывную модель. В этом случае можно зафиксировать амплитуды. Кроме квантования по времени можно квантовать и по вертикали (амплитуде). При таком виде квантования цифры заносятся в виде “0” и “1”. В случае объединения этих квантований они называются дискретными. 0 тогда имеем непрерывную модель. В этом случае можно зафиксировать амплитуды. Кроме квантования по времени можно квантовать и по вертикали (амплитуде). При таком виде квантования цифры заносятся в виде “0” и “1”. В случае объединения этих квантований они называются дискретными.Выделим случай, когда входной сигнал x(t) является элементарной функцией 1(t). Реакцию системы на воздействие 1(t) можно компактно: 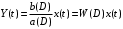 , (5.1) , (5.1) где W(D) называется операторной передаточной функцией или оператором. Формально W(D) можно рассматривать как дробно-рациональную функцию от оператора: 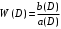 . (5.2) . (5.2)Воспользуемся преобразованием Лапласа, основываясь на утверждении 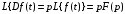 , (5.3) , (5.3) если f(0) = 0. Аналогично можно записать: 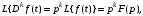 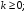 (5.4) (5.4)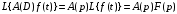 (5.5) (5.5)для любого операторного многочлена степени k, если f(t) и ее производные при t < 0, равны нулю. Применяя правило (5.5), получим 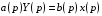 , (5.6) , (5.6) где 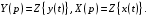 При этом предполагается, что равны нулю y(0), x(0) и начальные значения производных y(t), x(t) вплоть до (n – 1)-й и (m – 1)-й соответственно. Теперь a(p), b(p) обычные функции комплексной переменной p. Поэтому операция деления на a(p) имеет обычный смысл 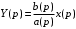 . (5.7) . (5.7)Учитывая определения (5.7), приходим к основной формуле 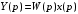 . (5.8) . (5.8)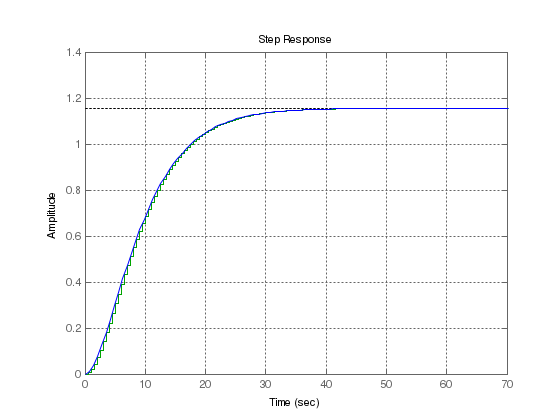 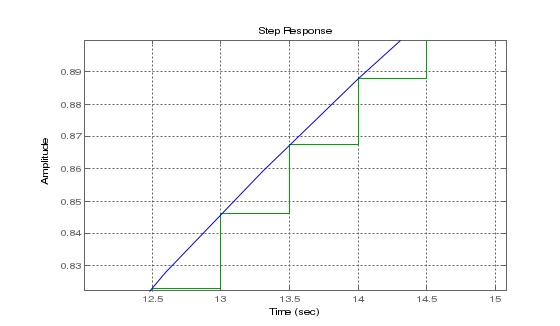 Рисунок 4.1 – Переходная характеристика непрерывной и дискретной систем с периодом квантования Т=0.5 (а) и увеличение участка (б). Определяем погрешность квантования: 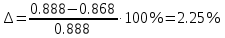 Погрешность квантования не превышает заданную (7%), значит выполняем переход от непрерывной модели к дискретной с периодом квантования 0.5. Передаточная функция в z-области: 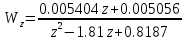 Программа перехода от непрерывной модели(модели в пространстве состояния ) к дискретной в пакете MATLAB clc, clear % задаем матрицы параметров A=[-0.2 0;0 -0.2] B=[0;0.1848] F=[0.25;0] C=[1 1] D=[0] BB=[B F] % переход в область переменных состояний sistema1=ss(A,BB,C,D) % переход в дискретную область sistema2=c2d(sistema1,0.5) Wz=tf(sistema2) Модель в пространстве состояний. a = x1 x2 x1 0.9048 0 x2 0 0.9048 b = u1 u2 x1 0 0.119 x2 0.08793 0 c = x1 x2 y1 1 1 d = u1 u2 y1 0  Передаточная функция в z-области по каналам. 1.По первому динамическому каналу. 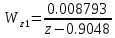 2.По второму динамическому каналу. 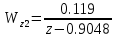 5 .Получение переходных функций объекта по передаточным функциям каналов.Переходной характеристикой(переходной функцией) h(t) называется реакция системы на единичное ступенчатое входное воздействие u(t-τ)=1(t-τ) при нулевых начальных условиях. Единичная ступенчатая функция – это функция, которая обладает свойством 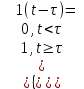 На рисунке 5.1 приведен пример переходной характеристики системы. 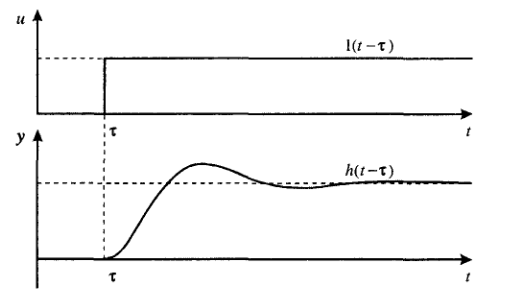 Рисунок 5.1-Пример переходной характеристики системы (τ – момент возникновения входного воздействия) Для аналитического определения переходной функции следует решить дифференциальное уравнение при нулевых начальных условиях и единичном входном воздействии. При исследовании реального объекта переходную характеристику можно получить экспериментальным путем, подавая на его вход ступенчатое воздействие и фиксируя реакцию на выходе. Если входное воздействие представляет собой неединичную ступенчатую функцию u(t)=k1(t), то выходная величина будет равнаy(t)=kh(t), т.е. представляет собой переходную характеристику с коэффициентом пропорциональности k[2]. Для построения переходной характеристики воспользуемся пакетом Matlab: clear,clc W1=tf([1.25],[0.05 1]); step(W) 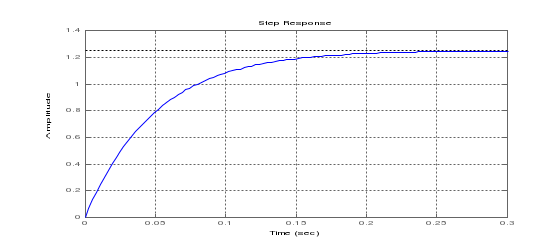 Рисунок 5.1- Переходная характеристика объекта по первому динамическому каналу 6. Расчет коэффициентов передаточной функции по экспериментальной переходной функции методом площадей. Сравнение результатов расчета с истинной (аналитической) передаточной функцией объекта.В основе метода площадей лежит предположение, что объект может быть описан линейным дифференциальным уравнением с постоянными коэффициентами, а его нормированная (приведенная к единице) переходная характеристика может быть аппроксимирована передаточной функцией вида: 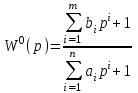 (6.1) (6.1)Порядок числителя в выражении (6.1) всегда меньше или равен порядку знаменателя. Для нахождения явного вида выражения (6.1) для конкретного технологического объекта необходимо определить значения коэффициентов ai и bi, а также значения степеней полиномов n и m. На первом этапе осуществляют нормирование переходной характеристики и входного воздействия: 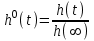 ; ; 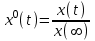 (6.2) (6.2)Искомые коэффициенты W0(p) определяются из системы уравнений: 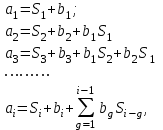 (6.3) (6.3)где i=m+nи для всех i>n ai=0, а для всех i>m bi=0. Входящие в эту систему уравнений коэффициенты S1, S2, …, Siсвязаны с кривой разгона интегральными соотношениями и вычисляются в соответствии с (4), где обозначено 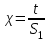 - относительное время.Для расчета S1, S2 … Siиспользуют численные методы (метод прямоугольников, метод трапеций и др.):[2] - относительное время.Для расчета S1, S2 … Siиспользуют численные методы (метод прямоугольников, метод трапеций и др.):[2]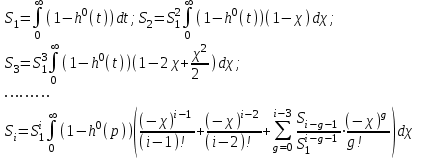 (6.4) (6.4)Переход от нормированной передаточной функции к обычной осуществляется путем ее умножения на коэффициент передачи 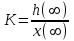 : :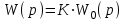 (6.5) (6.5)Таблица экспериментальных данных 6.1
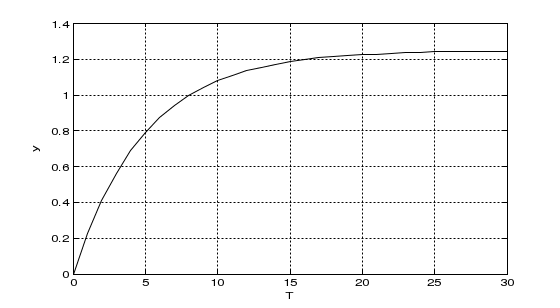 Рис.6-1. График переходной экспериментальной характеристики. 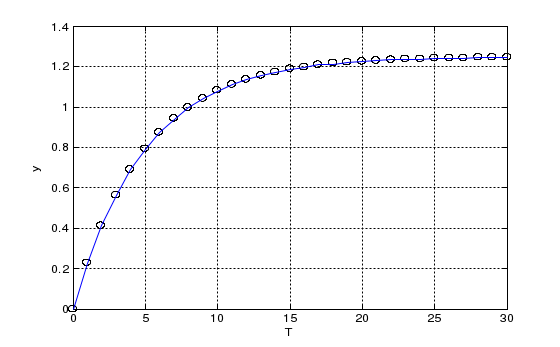 Рис. 6-2. Совмещённый график расчётной и экспериментальной переходной характеристики. В результате выполнения программы были получены следующие результаты: 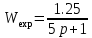 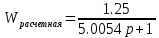 Как видно из рисунка 6.2, экспериментальная и рассчитанная переходные характеристики практически не отличаются. ЗаключениеВ данной курсовой работе была получена математическая модель теплообменника в виде дифференциальных уравнений. Также была получена передаточная функция объекта по заданному каналу (регулирование температуры подаваемой жидкости) и ее переходная характеристика. Для идеального случая (возмущения отсутствуют) и при наличии возмущений по двум другим каналам была получена модель в переменных состояния. А также по заданному каналу дискретная модель. По экспериментальной передаточной функции с помощью метода площадей была получена расчетная передаточная функция. Сравнение показало, что экспериментальная и расчетная передаточные характеристики практически не отличаются. Список использованной литературыПолоцкий Л. М., Лапшенков Г.И. «Автоматизация химических производств». Теория, расчет и проектирование систем автоматизации - М:Химия, 1982. – 296 с. Кузьмицкий, И.Ф., Кулаков Г.Т. Теория автоматического управления : учеб. пособие для студентов специальности «Автоматизация технологических процессов и производств». – Минск: БГТУ, 2006. – 486 Казаков А.В ,Кулаков М.В, Мелюшев Ю.К.Основы автоматики и автоматизации химических производств.Москва 1970.-374 Графический материал1. Схема объекта регулирования  2. Структурная схема  3. Переходная характеристика объекта по заданному динамическому каналу  4.Совмещённый график расчётной и экспериментальной переходной характеристики. 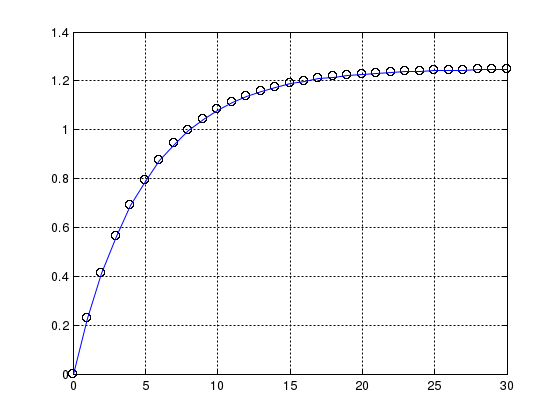 |