Линейная алгебра. 1. Решение а в
 Скачать 20.51 Kb. Скачать 20.51 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Линейная алгебра Группа Вл19Э27 Студент Ю.С. Медведева МОСКВА 2020 Задачи 1. Найти сумму матриц: 1.1. А = 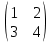 В = В = 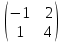 1.2. А = 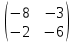 В = В = 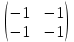 1. Решение: 1.1. А + В = 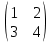 + + 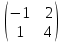 = = 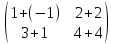 = = 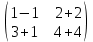 = = 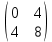 1.2. А + В = 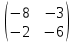 + + 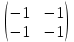 = = 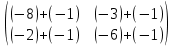 = = 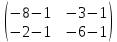 = = 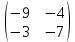 2. Найти произведение матриц 2.1. А = 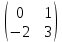 В = В = 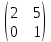 2.2. А = 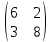 В = В = 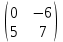 2. Решение: 2.1. C = A·B = 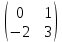 · · 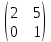 = = 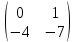 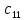 = = 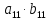 + +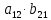 = 0 · 2 + 1 · 0 = 0 + 0 = 0 = 0 · 2 + 1 · 0 = 0 + 0 = 0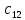 = =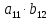 + +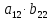 = 0 · 5 + 1 · 1 = 0 + 1 = 1 = 0 · 5 + 1 · 1 = 0 + 1 = 1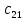 = =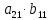 + +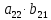 = (-2) · 2 + 3 · 0 = (-4) + 0 = -4 = (-2) · 2 + 3 · 0 = (-4) + 0 = -4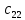 = =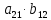 + +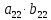 = (-2) · 5 + 3 · 1 = (-10) + 3 = -7 = (-2) · 5 + 3 · 1 = (-10) + 3 = -72.2. C = A·B = 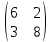 · · 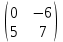 = = 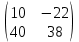 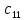 = = 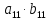 + +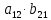 = 6 · 0 + 2 · 5 = 0 + 10 = 10 = 6 · 0 + 2 · 5 = 0 + 10 = 10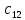 = =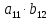 + +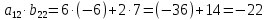 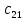 = =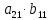 + +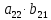 = 3 · 0 + 8 · 5 = 0 + 40 = 40 = 3 · 0 + 8 · 5 = 0 + 40 = 40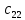 = =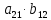 + +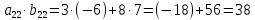 3. Найти определители матриц 3.1. А = 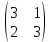 3.2. А = 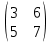 3. Решение: 3.1. det A = 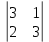 = 3·3 - 2·1 = 9 - 2 = 7 = 3·3 - 2·1 = 9 - 2 = 73.2. det A = 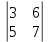 = 3·7 - 5·6 = 21 - 30 = -9 = 3·7 - 5·6 = 21 - 30 = -94. Решить систему уравнений 4.1. 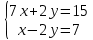 4.2. 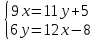 4. Решение: 4.1. 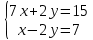 Поделим 1-ое уравнение на 7: 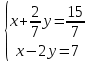 Из 1-ого уравнения выразим x через остальные переменные: 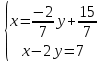 Во 2-е уравнение подставляем x 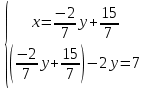 После упрощения получаем: 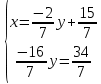 Поделим 2-ое уравнение на 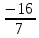 : :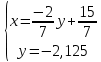 Теперь, двигаясь от последнего уравнения к первому, можно найти значения остальных переменных: 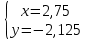 4.2. 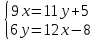 Приведем систему уравнений к каноническому виду: 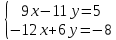 Упростим систему: 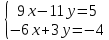 Поделим 1-ое уравнение на 9: 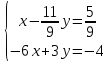 Из 1-ого уравнения выразим x через остальные переменные: 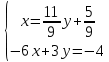 Во 2-е уравнение подставляем x: 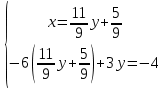 После упрощения получаем: 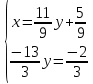 Поделим 2-ое уравнение на - 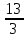 : :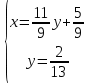 Теперь, двигаясь от последнего уравнения к первому, можно найти значения остальных переменных: 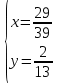 5. Для заданных векторов найти смешанное произведение 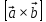 · · 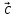 5.1. 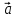 = (1; -2; 1) = (1; -2; 1) 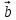 = (2; 1; -2) = (2; 1; -2) 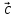 = (1; 1; 1;) = (1; 1; 1;)5.2. 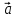 = (1; 1; 2) = (1; 1; 2) 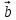 = (1; -1; 3) = (1; -1; 3) 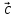 = (-2; -2; 2;) = (-2; -2; 2;)5. Решение: 5.1. 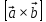 · · 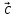 = = 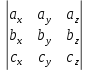 = = 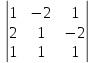 = 1·1·1 + (-2)·(-2)·1 + 1·2·1 - 1·1·1 - (-2)·2·1 - 1·(-2)·1 = 1 + 4 + 2 - 1 + 4 + 2 = 12 = 1·1·1 + (-2)·(-2)·1 + 1·2·1 - 1·1·1 - (-2)·2·1 - 1·(-2)·1 = 1 + 4 + 2 - 1 + 4 + 2 = 125.2. 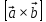 · · 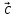 = = 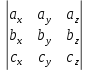 = = 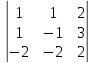 = 1·(-1)·2 + 1·3·(-2) + 2·1·(-2) - 2·(-1)·(-2) - 1·1·2 - 1·3·(-2) = -2 - 6 - 4 - 4 - 2 + 6 = -12 = 1·(-1)·2 + 1·3·(-2) + 2·1·(-2) - 2·(-1)·(-2) - 1·1·2 - 1·3·(-2) = -2 - 6 - 4 - 4 - 2 + 6 = -12 |
