ЗЛП Excel. 1. Решение задач линейного программирования с помощью поиска решений в среде Excel 1Задача оптимального использования ресурсов
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
Equation Chapter 1 Section 1 1.Решение задач линейного программирования с помощью поиска решений в среде Excel1.1Задача оптимального использования ресурсовПостановка задачи и основная формулаФабрика имеет в своём распоряжении определённое количество ресурсов: рабочую силу, деньги, сырьё, оборудование, производственные площади и т.п. Допустим, например, ресурсы трёх видов: рабочая сила, сырьё и оборудование – имеются в количестве соответственно 200 (чел/дней), 80 (кг) и 140 (станко/ч). Фабрика может выпускать изделия трёх видов. Информация о количестве единиц каждого ресурса, необходимых для производства одного каждого вида, и доходах, получаемых предприятием от единицы каждого вида товаров, приведена в таблице. Таблица2.1 – Оптимального использования ресурсов
Требуется найти такой план выпуска продукции, при котором будет максимальная общая стоимость продукции. Обозначим через Х1, Х2, Х3, количество изделий каждого типа. Целевая функция - это доход, который необходимо максимизировать: 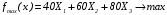 \* MERGEFORMAT () \* MERGEFORMAT () Ограничения по ресурсам 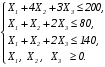 \* MERGEFORMAT () \* MERGEFORMAT ()1.2Решение задач линейного программирования с помощью поиска решений.Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. Чтобы активировать надстройку необходимо нажать (слева вверху) кнопку "Office" → Параметры Excel → Надстройки. В пункте Управление (внизу) нажать Перейти. В появившемся окне следует поставить галочку на пункте Поиск решения. Затем нажать ОК. Рассмотрим методику использования надстройки на выше указанном примере. 2.Подготовим форму для ввода условий ( Рисунок 1 ). 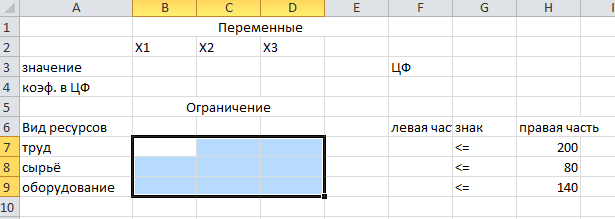 Рисунок 1 - Введена форма для ввода данных В нашей задаче оптимальные значения вектора Х=(Х1, Х2, Х3) будут помещены в ячейках В3:Е3, оптимальное значение целевой функции – в ячейке F4. 3.Введём исходные данные согласно модели и в созданную форму. Получим результат, показанный на рисунке 2. 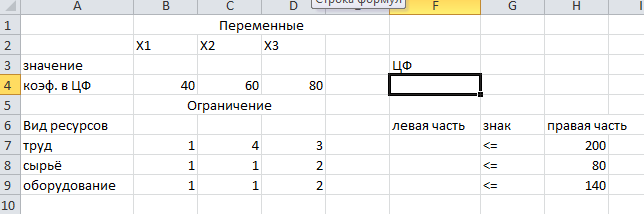 Рисунок 2 - Данные введены 4.Введём формулу для вычисления целевой функции:
5.Введём формулы для вычисления левых частей ограничений:
На этом ввод зависимостей закончен. 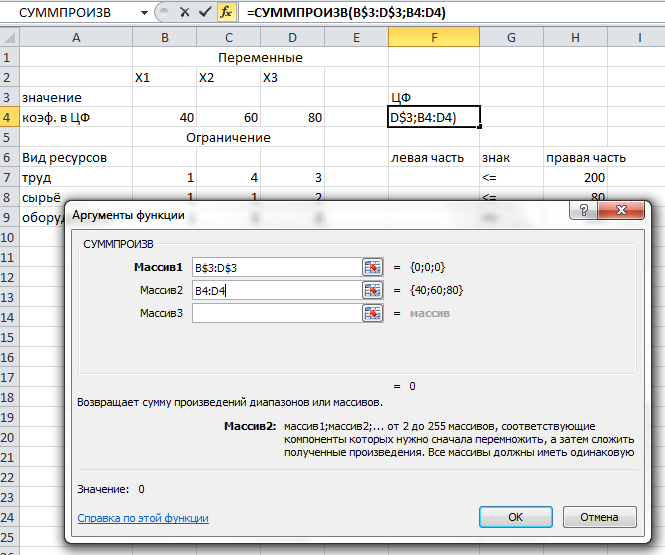 Рисунок 3 - Вводится функция для вычисления целевой функции. Запуск Поиска решенияПосле выбора команд Данные → Поиск решения появится диалоговое окно Поиск решения. В диалоговом окне Поиск решения есть три основных параметра:
Сначала нужно заполнить поле «Установить целевую ячейку». Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или же установить конкретное значение. Второй важный параметр средства Поиск решения – это параметр Изменяя ячейки. Изменяемые ячейки – это те ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. Для поиска решения можно указать до 200 изменяемых ячеек. К изменяемым ячейкам предъявляется два основных требования: они не должны содержать формул, и изменение их значений должно отражаться на изменении результата в целевой ячейке. Другими словами, целевая ячейка зависима от изменяемых ячеек. Третий параметр, который нужно вводить для Поиск решений – это Ограничения. 6. Установить целевую ячейку (Назначение целевой функции)
7.Ввести адреса искомых переменных:
8.Ввод ограничений.
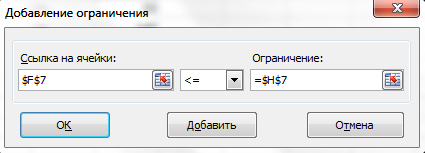 Рисунок 4 - Ввод правых и левых частей ограничений
На экране появится диалоговое окно Поиск решения с введёнными условиями (рисунок 5). 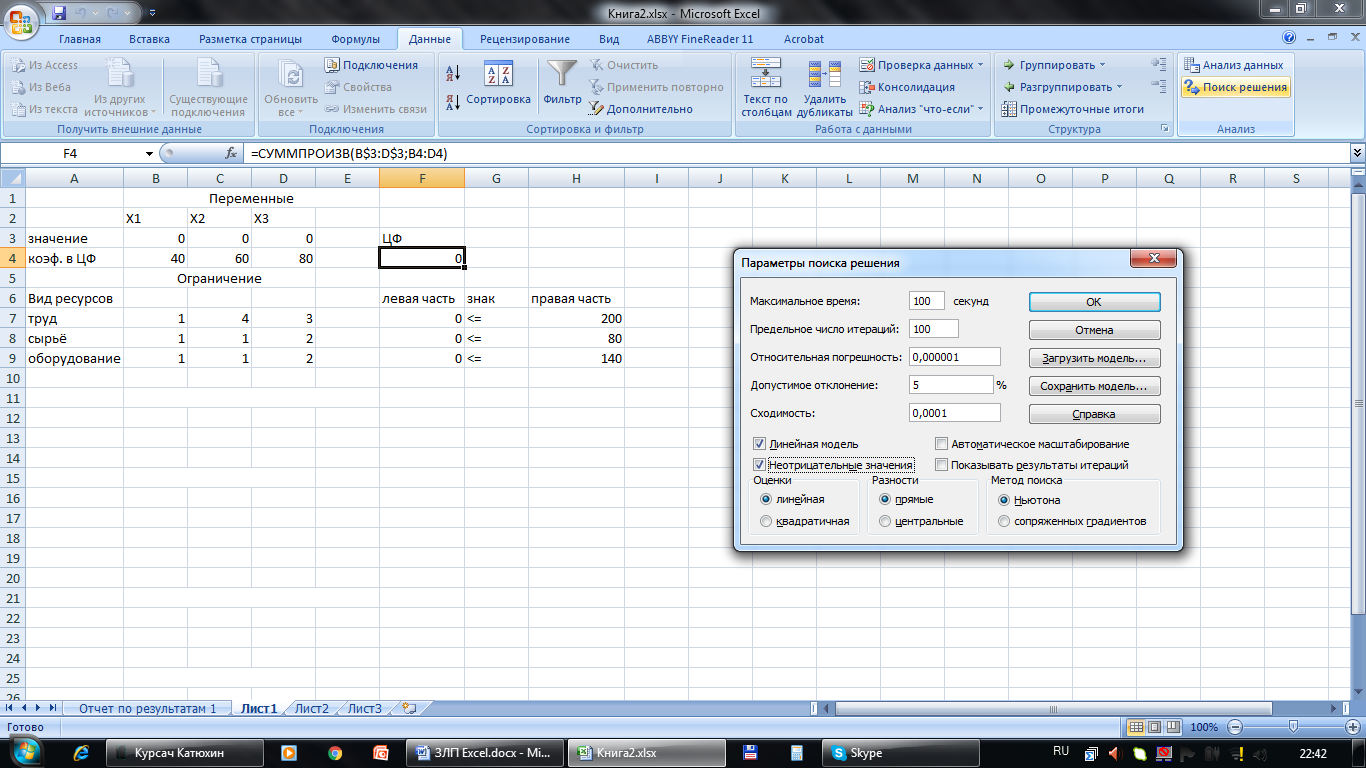 Рисунок 5 - Введены все условия для решения задачи 9.Ввод параметров для решения задачи линейного программирования (рисунок 6).
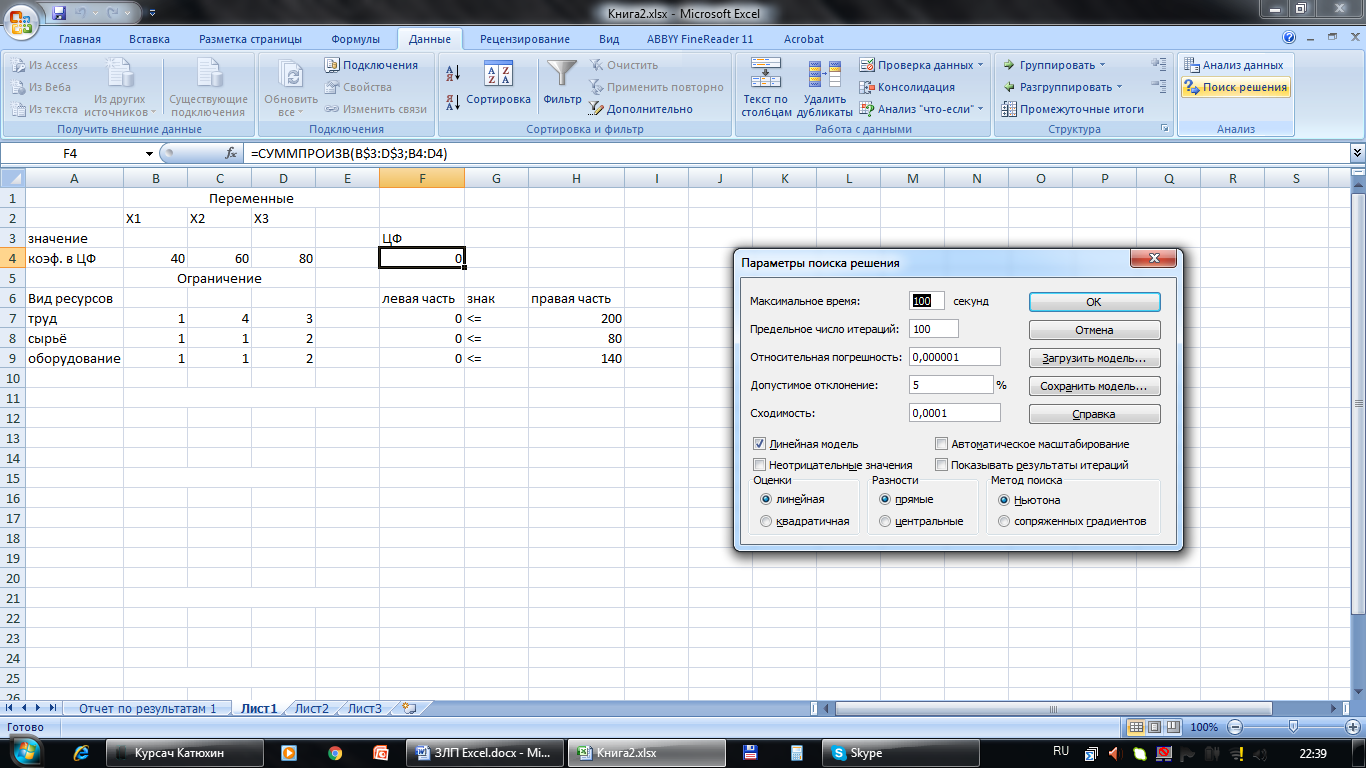 Рисунок 6 - Ввод параметров
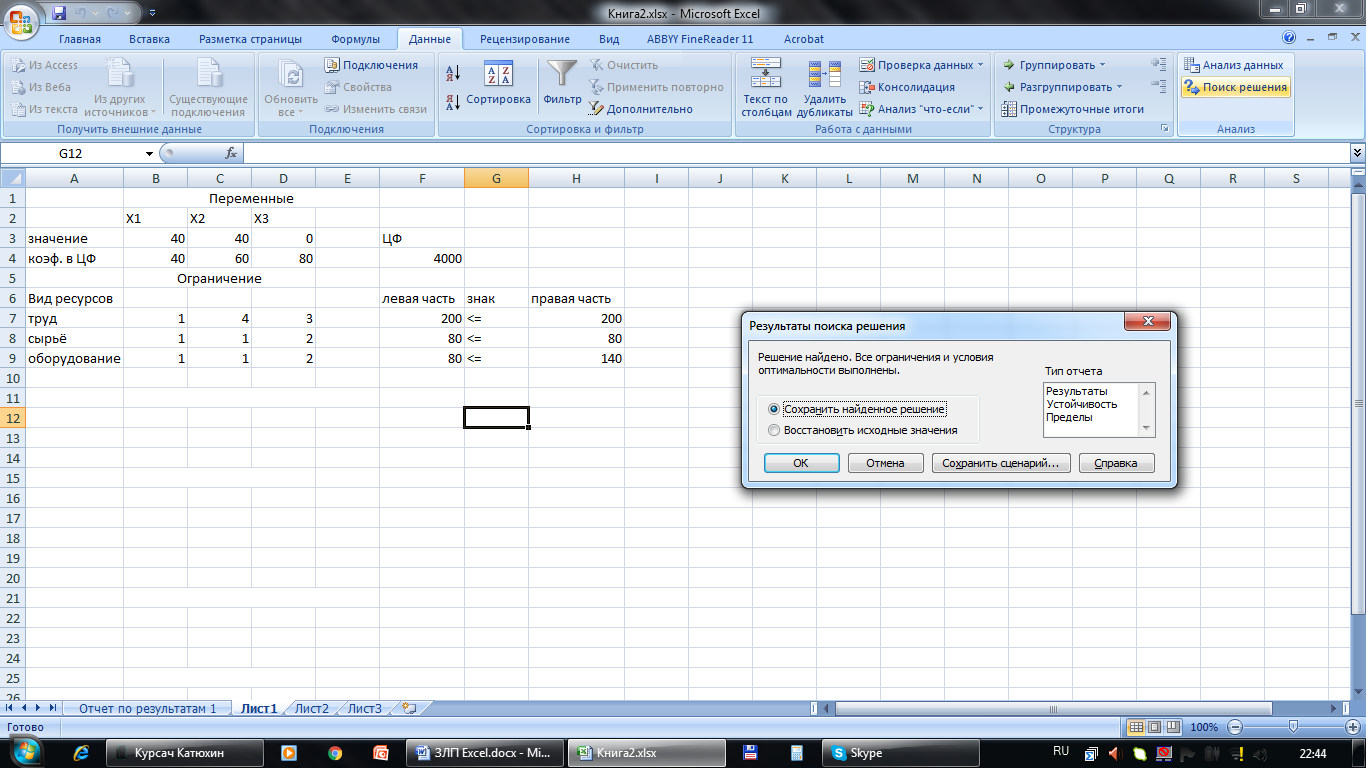 Рисунок 7 - Решение найдено Полученное решение означает, что максимальный доход 4000 руб. фабрика может получить при выпуске 40 изделий первого вида и 40 изделий второго вида. При этом ресурсы труд и оборудование будут использованы полностью, а из 140 (станко/ч) оборудования будет использовано 80 (станко/ч). 9.1Создание отчета по результатам поиска решенияEXCEL позволяет представить результаты поиска решения в форме отчета. Существует три типа таких отчетов: Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях. 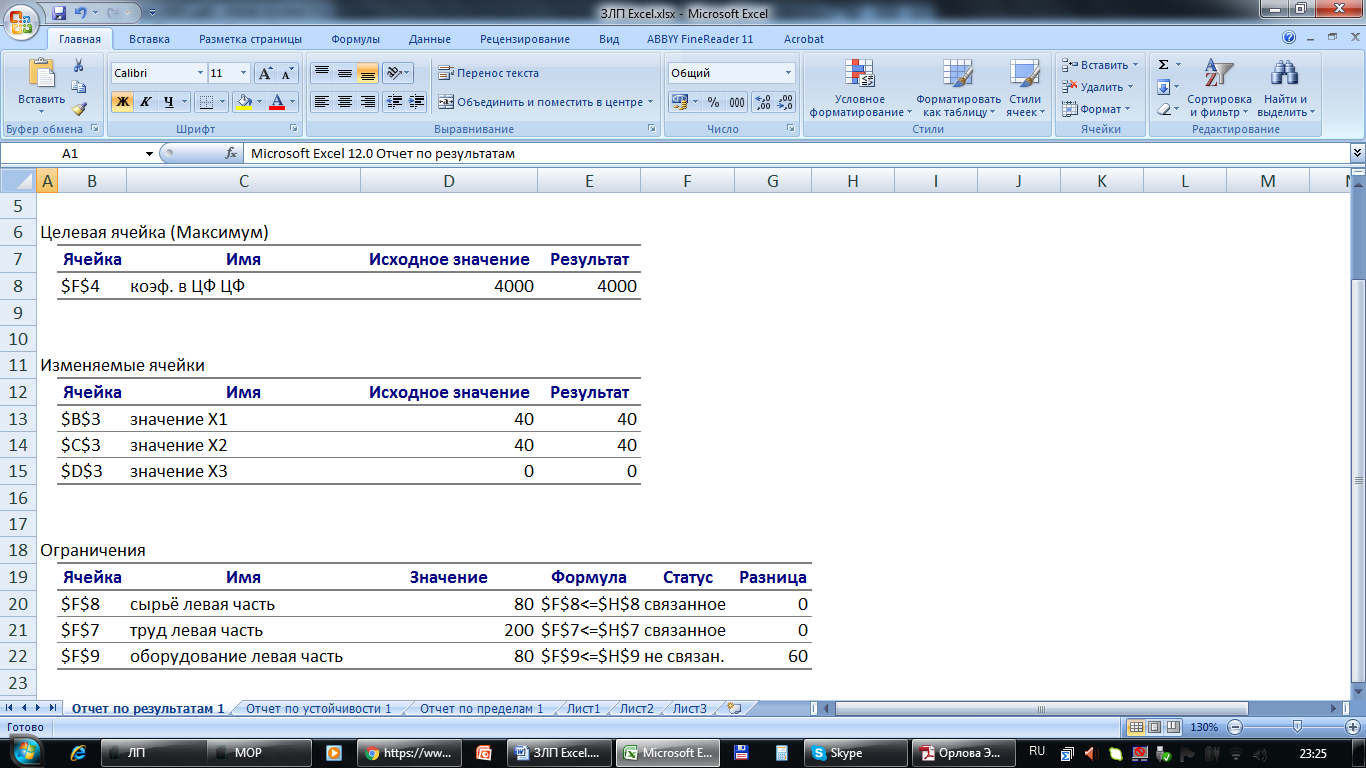 Рисунок 8 - Отчет по результатам Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений. 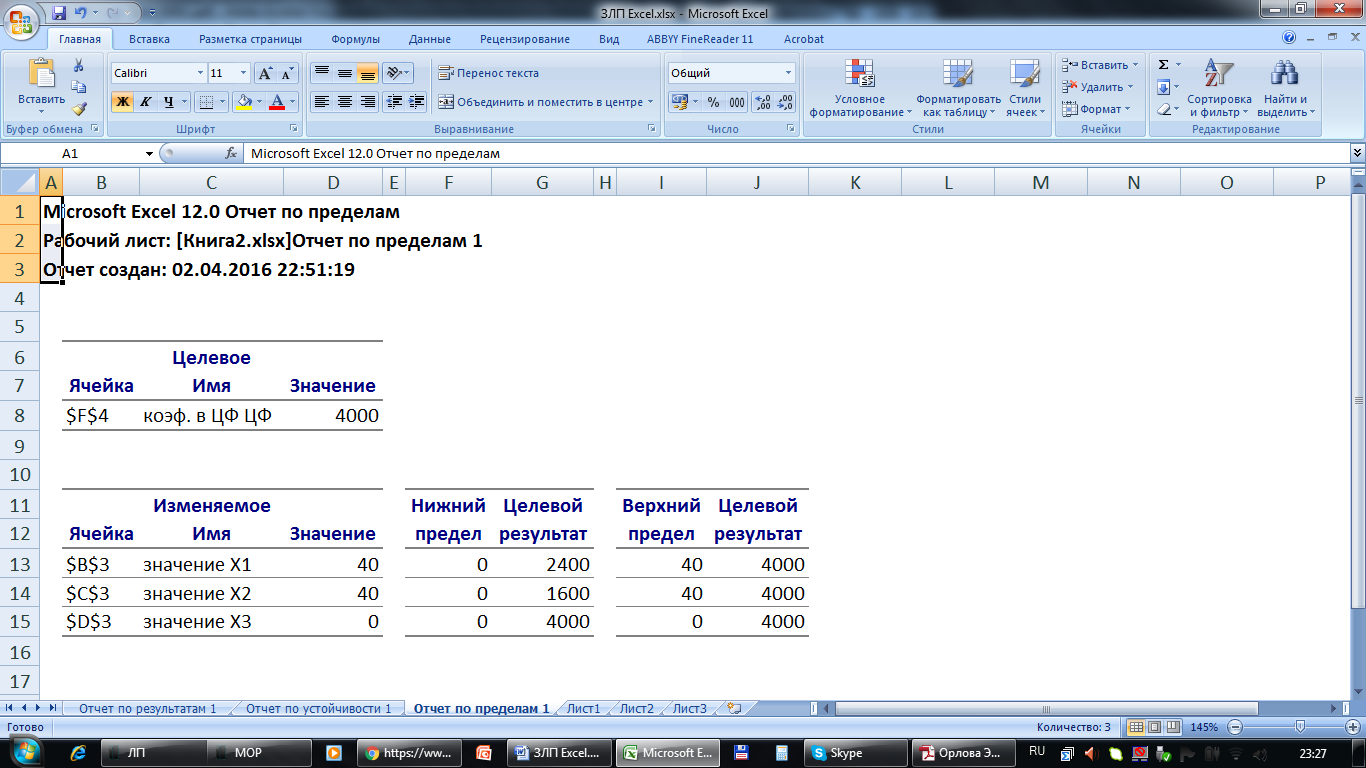 Рисунок 9 - Отчет по пределам Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений. 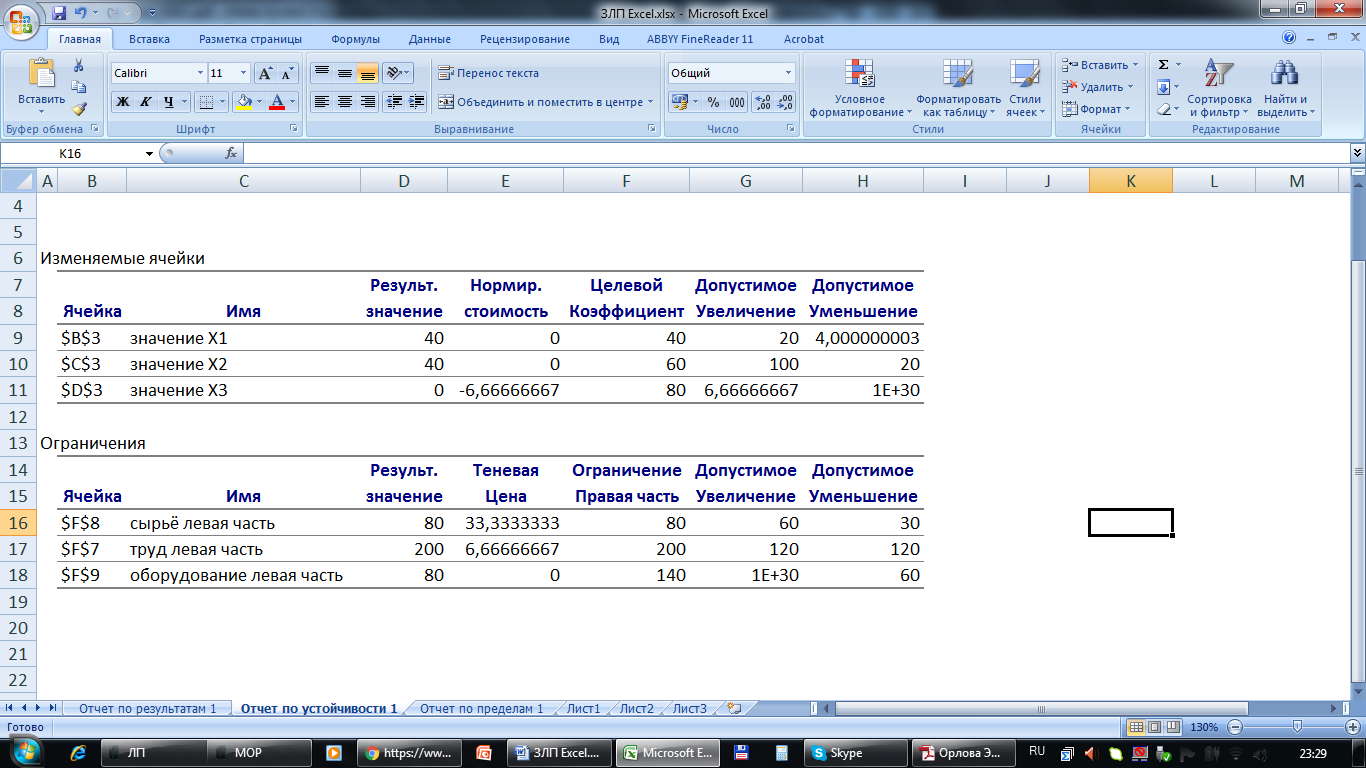 Рисунок 10 - Отчет по устойчивости Именно в Отчете по устойчивости можно найти решение двойственной задачи. Теневые цены ресурсов труд, сырье и оборудование соответственно равны 4/3, 0, 1/3 или в десятичных дробях: 1,3333; 0; 0,3333. Библиографический список
| ||||||||||||||||||
