Вариант. 1. Решите уравнение Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию А сумма очков равна 5
 Скачать 106.68 Kb.
|
|
Вариант № 46987460 1. Решите уравнение  2. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»? 3. Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 108°. Найдите число вершин многоугольника. 4. Найдите  если  5. Найдите объем многогранника, вершинами которого являются точки A, B, C,  п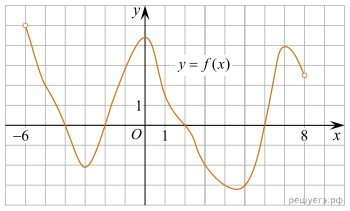рямоугольного параллелепипеда  у которого    6.  На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.7. Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы:  где t − время в минутах,  К,  К/мин  К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.8. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч. 9.  На рисунке изображён график функции вида  где числа a, b и c — целые. Найдите  10. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98? В ответе укажите наименьшее необходимое количество выстрелов. 11. Найдите точку минимума функции  12. a) Решите уравнение  б) Укажите корни этого уравнения, принадлежащие промежутку  13. Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α содержащей прямую BD1 и параллельной прямой AC, является ромб. а) Докажите, что грань ABCD — квадрат. б) Найдите угол между плоскостями α и BCC1, если AA1 = 6, AB = 4. 14. Решите неравенство: 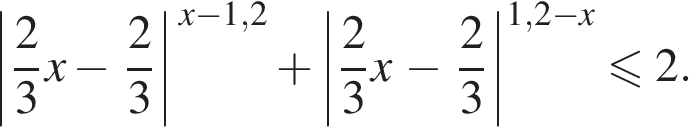 15. Два брокера купили акции одного достоинства на сумму 3640 р. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 р. Первый брокер продал 75% своих акций, а второй 80% своих. При этом сумма от продажи акций, полученная вторым брокером, на 140% превысила сумму, полученную первым брокером. На сколько процентов возросла цена одной акции? 16. В остроугольном треугольнике ABC провели высоту BH, из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно. а) Докажите, что треугольник MBK подобен треугольнику ABC. б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4. 17. Найдите все значения a, при каждом из которых система уравнений 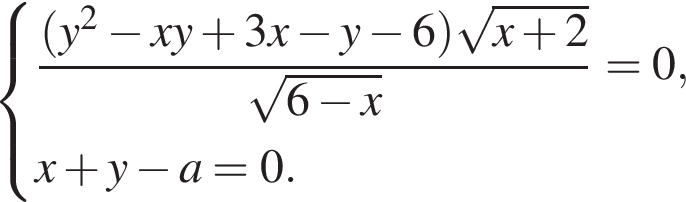 имеет ровно два различных решения. 18. а) Можно ли число 2014 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр? б) Можно ли число 199 представить в виде суммы двух различных натуральных чисел с одинаковой суммой цифр? в) Найдите наименьшее натуральное число, которое можно представить в виде суммы пяти различных натуральных чисел с одинаковой суммой цифр. |