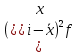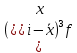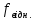РАСЧЕТНАЯ РАБОТА. Расчетная работа. 1. Содержание задания (для студентов всех специальностей)
 Скачать 31.32 Kb. Скачать 31.32 Kb.
|
|
Вариант №19 1. Содержание задания (для студентов всех специальностей) 1. С помощью аналитической группировки с равными интервалами и определите наличие зависимости между результативным и факторным признаками (lg20 = 1,3). Сделайте выводы относительно зависимости между показателями. 2. Проведите структурную группировку совокупности по факторным признаком. Сделайте выводы. 3. По интервальным вариационным рядом факторного признака рассчитайте: а) показатели центра распределения: среднее значение, моду и медиану; б) показатели структуры распределения: первый, девятый децілі и коэффициент децільної дифференциации, коэффициент Джини; в) показатели вариации: дисперсию и коэффициент вариации; г) показатели формы распределения: коэффициенты асимметрии и эксцесса. По каждому подпункту задачи сделайте выводы. Варианты заданий содержатся в таблице 1 приложения. Исходные данные:
1.Рассчитываем число групп по формуле Старджесса: L = 1+3,322lgn = 1+ 3,322lg20=5 Тогда величина интервала группировки по факторному признаку Х « стоимость основных фондов предприятия» равна:  = (7,0-2,0)/5 = 1 млн.грн. = (7,0-2,0)/5 = 1 млн.грн.тогда интервалы будут такими: 2,0-3,0 3,0-4,0 4,0-5,0 5,0-6,0 6,0-7,0 Составляем структурную группировку предприятий по признаку «стоимость основных фондов предприятий»
Из расчетных данных прослеживается прямая зависимость между стоимостью основных фондов предприятия (факторный признак х) и выпуском продукции (результативный признак у). Так с увеличением стоимости основных фондов предприятия по каждой группе увеличивается соответственно выпуск продукции Составляем аналитическую группировку предприятий по признаку «стоимость основных фондов»
С увеличением стоимости основных фондов предприятия наблюдается рост выпуска продукции.
I:  II:  , III: , III: 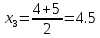 , IV: , IV:  , V: , V:  = 6.5 = 6.5Рассчитываем среднюю стоимость основных фондов предприятия: 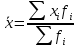 = 79/20 = 3,95 млн.грн. = 79/20 = 3,95 млн.грн.Рассчитываем моду:  = 3+1 = 3+1 = 3,45 млн.грн. = 3,45 млн.грн.Большинство предприятий имеют стоимость основных фондов в размере 3,45 млн.грн. Рассчитаем медиану:  = 3+1 = 3+1 = 2,66 млн.грн. = 2,66 млн.грн.У половины предприятий, стоимость основных фондов не превышает 2,66 млн. грн., а у другой половины предприятий, стоимость основных фондов, стоимость соответственно выше 2,66 млн.грн. Вычисляем дисперсию:  Находим среднеквадратическое отклонение:  = 1,203 млн.грн. = 1,203 млн.грн.Находим коэффициент вариации: V =  *100% = *100% = 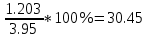 Из расчетных данных среднеквадратического отклонения и коэффициента вариации можно сказать, что совокупность предприятий относительно стоимости основных фондов предприятий однородная, средняя типична и ей можно доверять. Децильный коэффициент дифференциации стоимости основных фондов предприятий, характеризующийся, во сколько раз минимальная стоимость 10% стоимости основных фондов предприятий превышают максимальную стоимость 10% стоимости основных фондов предприятий:  , где , где 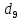 – девятый дециль распределения; – девятый дециль распределения; – первый дециль распределения. – первый дециль распределения.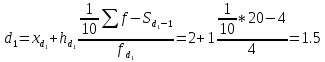 млн.грн. млн.грн.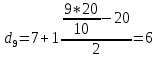 млн.грн. млн.грн. , т.е. значение коэффициента означает, что в 4 раза минимальная стоимость 10% предприятий стоимости основных фондов, что имеют наибольшую стоимость, выше стоимости основных фондов 10% предприятий, что имеют наименьшую стоимость основных фондов. , т.е. значение коэффициента означает, что в 4 раза минимальная стоимость 10% предприятий стоимости основных фондов, что имеют наибольшую стоимость, выше стоимости основных фондов 10% предприятий, что имеют наименьшую стоимость основных фондов.Для количественной оценки уровня концентрации рассчитываем коэффициент концентрации Джини: 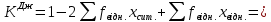 1-2*0,0549675+0,026075 = 0,916 1-2*0,0549675+0,026075 = 0,916Коэффициент Джини приблизился к единице, что свидетельствует о значительном расслоении стоимости основных фондов предприятий. Таблица «Кумулятивные показатели распределения предприятий по стоимости основных фондов.»
Рассчитываем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, то есть 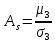 где 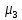 – центральный момент третьего порядка, рассчитываем по формуле – центральный момент третьего порядка, рассчитываем по формуле 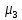 = 28,095/20 = 1,40475 = 28,095/20 = 1,40475 = 1,40475/ = 1,40475/ = 0,81 = 0,81Так как величина асимметрии положительна, следовательно, речь идет о правосторонней асимметрии. Полученный результат свидетельствует о наличии несущественной по величине и положительной по своему характеру асимметрии. Далее рассчитаем показатель эксцесса. Наиболее точно он определяется по формуле с использованием центрального момента четвертого порядка 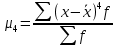 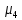 = 114,434625/20 = 5,72173125 = 114,434625/20 = 5,72173125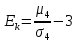 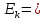 114,434625/ 114,434625/ – 3 = 54,64 – 3 = 51,64 – 3 = 54,64 – 3 = 51,64Так как  распределение является островершинным. распределение является островершинным. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

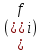
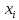

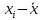 )
)