статистика. Задачи по теме Средние величины Показатели вариации рядов ра. Задача 1 По следующим данным о распределении 100 рабочих цеха по дневной выработке однотипных изделий определите моду и медиану

• Название: Задача 1 По следующим данным о распределении 100 рабочих цеха по дневной выработке однотипных изделий определите моду и медиану
• Анкор: статистика
• Дата: 30.03.2021
• Размер: 144.5 Kb.
• Имя файла: Задачи по теме Средние величины Показатели вариации рядов ра.doc
• Тип: Задача; #189451

Задачи по теме «Средние величины», «Показатели вариации рядов распределения»
Задача 1

По следующим данным о распределении 100 рабочих цеха по дневной выработке однотипных изделий определите моду и медиану:

Дневная выработка, шт	50-54	54-58	58-62	62-66	66-70
Число рабочих, чел	10	20	40	15	15

Решение:

Определим моду:





Определим медианный интервал. Им считается тот, до ко­торого сумма накопленных частот меньше половины всей чис­ленности ряда, а с прибавлением его численности - больше половины. Подсчитаем накопленные итоги частот: 10, 30, 70, 85, 100. Середина накопленных частот - 100/2 = 50. Сумма первых двух меньше половины (30 < 50), а если прибавить 40 - больше половины численности совокупности (70 > 50). Следовательно, медианным является интервал - 58-62. Оп­ределим медиану: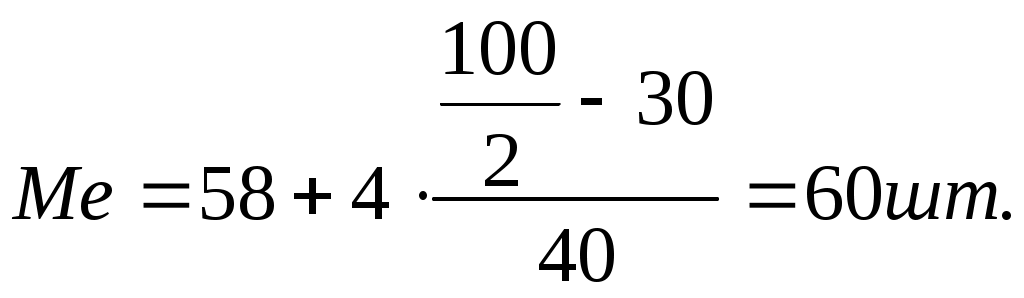





Итак, 50% рабочих вырабатывают в день меньше 60 изде­лий, а остальные 50% - более 60 шт.
Задача 2

Имеются следующие данные о заработной плате рабочих цеха, представленные в таблице

№	Заработная плата, руб.	Количество рабочих, чел	Среднее значение интервала
1	2	3	4	5	6
1	1500-2000	7	1750	12250	4.729.788
2	2000-2500	12	2250	27000	1.244.208
3	2500-3000	16	2750	44000	506.944
4	3000-3500	10	33250	32500	4.596.840
5	Итого	45		115750	11.077.780

Определите среднюю заработную плату рабочих и показатели вариации.
Решение:

Средняя заработная плата рабочих определяется по формуле по формуле среднеарифметическая взвешенной:

(руб.)

Размах вариации заработной платы определяем по формуле:

Дисперсию определяем по формуле:

Среднее квадратическое отклонение определяем по формуле:

Коэффициент вариации определяем по формуле: %

Так как коэффициент вариации , то совокупность считается однородной и средняя заработная плата представляет её типичный уровень оплаты труда в цехе.

Задача 3

По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели, представленные в таблице

№	Отрасль	Средняя заработная плата, руб.	Численность работников, чел.	Дисперсия заработной платы
1	2	3	4	5
1	Здравоохранение	600	80	4900
2	Образование	800	120	16900
3	Итого	-	-	-

По приведенным данным определите:

1. 
   общую среднюю заработную плату работников по двум отраслям;
   
2. 
   общую, межгрупповую и среднюю из внутригрупповых дисперсий;
   
3. 
   коэффициент детерминации и эмпирическое корреляционное отношение;
   
4. 
   сделайте выводы.
   

Решение:

Общая средняя заработная плата по двум отраслям составит:

руб.

Средняя из внутригрупповых дисперсий составит:



Межгрупповая дисперсия составит:



Применяя правило сложений дисперсий, определяем общую дисперсию:



Коэффициент детерминации составит:



Эмпирическое корреляционное отношение составит: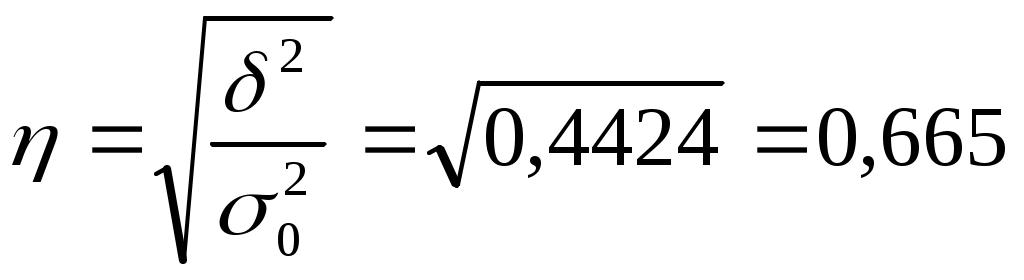



Вывод: существует средняя по силе тесноты связи между уровнем заработной платы и отраслью.
Задача 4

По данным обследования коммерческих банков города, 70% общего числа клиентов составили юридические лица со средним размером кредита 120 тыс. руб. и коэффициентом вариации 25% , и 30% - физические лица со средним размером ссуды 20 тыс. руб. при среднем квадратическом отклонении 6 тыс. руб.

Используя правило сложений дисперсий, определите тесноту связи между размером кредита и типом клиента, вычислить эмпирическое корреляционное отношение, и сделать выводы.

Решение:

Средний размер кредита по всем клиентам составит:

(руб.)

Межгрупповая дисперсия составит:

млн.руб.

Среднеквадратическое отклонение кредитов для юридических лиц составит:



Внутригрупповая дисперсия кредитов для юридических лиц будет равна:

млн.руб.

Внутригрупповая дисперсия ссуды для физических лиц составит:

млн.руб.

Средняя из внутригрупповых дисперсий составит:

млн.руб.

Общая дисперсия кредитов составит:

млн.руб.

Эмпирическое корреляционное отношение составит:



Так как - что свидетельствует о тесной связи между размером кредита и типом клиента.
Задача 5

Имеются следующие данные о распределении рабочих по размеру заработной платы:

№	Заработная плата рабочих, руб. в час	Число рабочих, чел
		Мужчины	Женщины	Всего
1	2	3	4	5
1	До 120	3	1	4
2	120-140	17	8	25
3	140-160	20	12	32
4	160-180	35	40	75
5	180 и более	15	35	50
6	Итого	90	96	186

Рассчитайте все показатели вариации по общей численности рабочих и определите, влияет ли пол рабочего на размер оплаты труда.
Решение:

Средняя заработная плата мужчин 159,3 руб. средняя заработная плата женщин 170,8 руб. средняя заработная плата 165,2 руб.

Размах вариации: руб.

Среднее линейное отклонение:

= 17,2 руб.

Дисперсия:



Среднее квадратическое отклонение: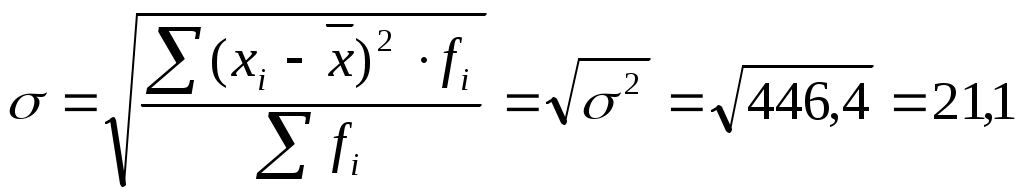

руб.

Коэффициент вариации:



Рассчитаем следующие виды дисперсий:

Внутригрупповая дисперсия для мужчин:





Внутригрупповая дисперсия для женщин:





Средняя из внутригрупповых дисперсий:



Межгрупповая дисперсия: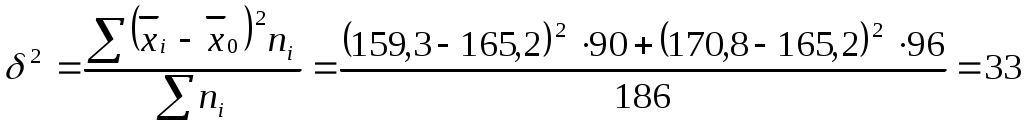



Общая дисперсия по правилу сложений дисперсий:



Эмпирическое корреляционное отношение:



Таким образом, пол рабочих не влияет на размер оплаты труда.