1 Составление уравнений вертикальных колебаний расчетной модели
 Скачать 120.84 Kb. Скачать 120.84 Kb.
|
|
1.4. Составление уравнений вертикальных колебаний расчетной модели. Схема замещения для подрессоренной части модели представлена на рисунки 1.2. 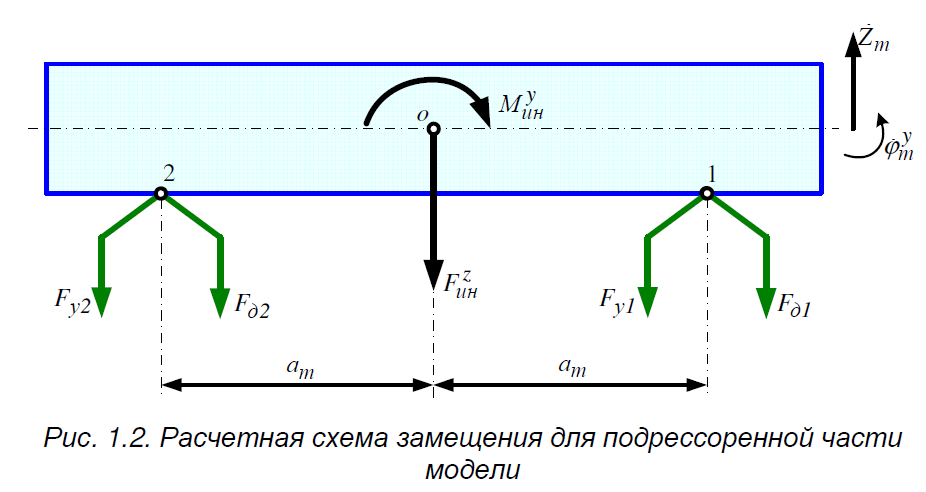 Запишем уравнение колебания подпрыгивания: 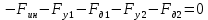 , (1.5) , (1.5)Входящие в это уравнение силы: – сила инерции подрессоренной части модели по оси 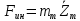 , (1.6) , (1.6)где 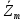 – вертикальное ускорение подпрыгивания модели; – вертикальное ускорение подпрыгивания модели;– сила упругости в первом комплекте РП 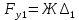 , (1.7) , (1.7)где 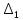 – деформация упругой связи первого комплекта РП (прогиб); – деформация упругой связи первого комплекта РП (прогиб);– сила диссипации в первом комплекте РП 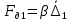 , (1.8) , (1.8)где 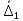 – скорость деформации упругой связи первого комплекта РП (скорость прогиба). – скорость деформации упругой связи первого комплекта РП (скорость прогиба).- разность перемещений крайних точек пружины 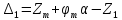 ; ;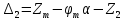 . (1.9) . (1.9)Соответственно скорости прогибов 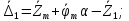 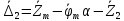 . (1.10) . (1.10)Подставим известные силы в уравнение (1.5): 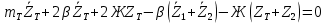 Для составления уравнения колебания галопирования рамы модели необходимо найти сумму моментов сил относительно оси Y, которое имеет вид: 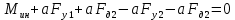 (1.11) (1.11)где 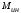 - главный момент сил инерции подрессоренной части модели относительно оси Y, который определяется: - главный момент сил инерции подрессоренной части модели относительно оси Y, который определяется: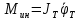 (1.12) (1.12)Подставляя уравнения (1.6) - (1.10) и (1.12) в уравнение (1.11) получим уравнение колебания галопирования модели: 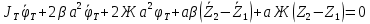 (1.13) (1.13)Для составления уравнения колебаний подпрыгивания колесных пар и пути используется схема замещения, которая для первой колесной пары будет иметь вид, представленный на рис 1.3. 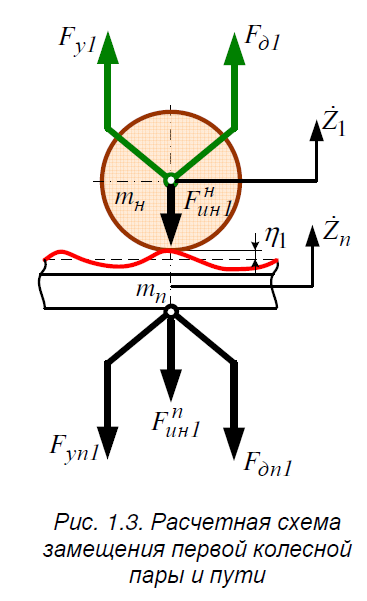 Для составления уравнения колебания подпрыгивания колесной пары и пути необходимо найти сумму проекций сил на ось Z: 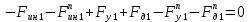 (1.14) (1.14)Входящие в это уравнение силы находятся: − сила инерции неподрессоренной массы по оси Z: 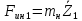 (1.15) (1.15)где 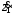 - вертикальное ускорение подпрыгивания первой колесной пары; - вертикальное ускорение подпрыгивания первой колесной пары;− сила инерции приведенной массы пути по оси Z: 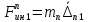 (1.16) (1.16)где 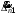 - ускорение деформации пути под первой колесной парой; - ускорение деформации пути под первой колесной парой;− сила упругости пути под первой колесной парой: 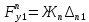 (1.17) (1.17)где 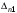 - деформация (прогиб) пути под первой колесной парой; - деформация (прогиб) пути под первой колесной парой;− сила упругости пути под первой колесной парой: 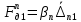 (1.18) (1.18)где 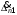 - скорость деформации пути под первой колесной парой. - скорость деформации пути под первой колесной парой.Деформация пути определяется под первой и второй колесными парами: 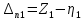 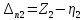 (1.19) (1.19)Подставляя уравнения (1.6) - (1.10), (1.15) – (1.19) в уравнение (1.14) и приводя подобные слагаемые получим уравнения колебания подпрыгивания для первой колесной пары и пути: 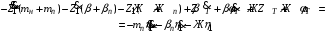 Аналогичным образом получаем уравнение колебания подпрыгивания второй колесной пары и пути, заменяя индексы сил на рисунке 1.3 на 2 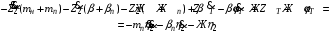 Все полученные уравнения колебаний подрессоренной части и колесных пар сводим в одну систему уравнений, в следующей последовательности: 1-е уравнение – подпрыгивание 1 КП, 2-е подпрыгивание 2 КП, 3-е – подпрыгивание рамы модели и 4-е – галопирование рамы модели. 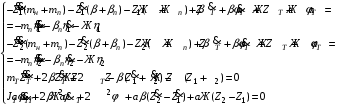 |
