Курсовая 3318113. 1 Спектральный анализ дискретизируемого сигнала
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Для выбранных параметров дискретизатора (F=2 кГц) и частоты среза восстанавливающего фильтра (FC=1 кГц) погрешность, рассчитанная с учетом задержки сигнала фильтром на время tз=0.42 мс, составляет 11.87%. По техническому заданию требуется обеспечить погрешность восстановления 1%. Таким образом, выбранные значения частот дискретизации и среза фильтра оказались несоответствующими требованиям технического задания и нуждаются в корректировке. Поэтому займемся исследованием зависимости погрешности сигнала d от значений частот F и FС с целью выборы их оптимальных значений. Критерием оптимальности служит значение погрешности восстановления равное 1%. 5 Исследование влияния на погрешность восстановления сигнала частоты его дискретизации и частоты среза ФНЧ. Обоснование и выбор оптимальных значений частот, обеспечивающих качество восстановления сигнала, соответствующее требованию технического задания Для построения зависимости погрешности восстановления от двух частот воспользуемся вычислительным пакетом MathCad, позволяющим строить графики функций двух переменных. Такие функции отображаются в трехмерной системе координат в виде поверхности. Чтобы построить график зависимости погрешности восстановления от частот среза и дискретизации можно использовать формулу 39, модифицировав ее, так как теперь частоты Fc и F являются переменными. Время задержки определим для нулевой частоты f=0 как функцию частоты среза фильтра. Тогда получим формулу (21). 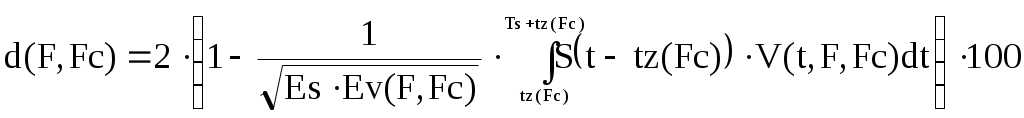 (21) (21)Входящие в формулу (21) величины и функции: время запаздывания, импульсная характеристика фильтра, число отсчетов, энергия исходного сигнала, восстановленный сигнал и энергия восстановленного сигнала - определяются соответственно по формулам (22)-(27). 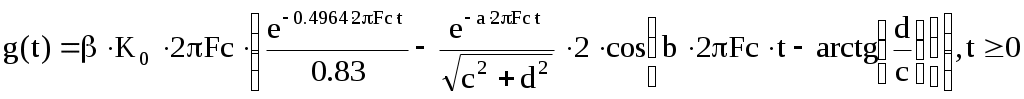 (23) (23)Для построения графика зададимся следующими интервалами частот: частоты среза фильтра – Fc ϵ [1;7] и частоты дискретизации Fϵ[2;15]. Значения частот выражены в килогерцах. График зависимости погрешности восстановления от частоты среза фильтра и от частоты дискретизации в виде диаграммы изображен на рисунке 16. В таблице 1 представлены результаты численного расчета погрешности восстановления, дублирующие графические зависимости. 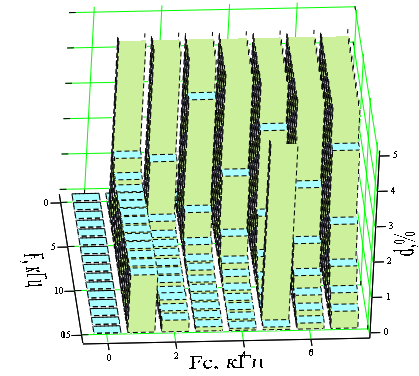 Рисунок 16 – Зависимость погрешности восстановления от частот среза фильтра и дискретизации Таблица 1 – Погрешность восстановления как функция частот среза фильтра и дискретизации
Из таблицы 1 определяем значения частот – Fc=2 кГц и F=5 кГц, при которых погрешность восстановлении d=0.63%. Таким образом, на данном этапе подобрали оптимальные частоты, обеспечивающие требуемую погрешность восстановления. 6 Расчет характеристик дискретизированного и восстановленного сигналов при оптимальных значениях частоты дискретизации и полосы пропускания ФНЧ. Сравнительный анализ качества восстановления сигнала заданным реальным фильтром и идеальным ФНЧ На рисунке 16 изображены графики исходного непрерывного (штриховая линия) и восстановленного с использованием оптимальных частот сигналов. На рисунках 17 и 18 показаны частотные характеристики этих сигналов. Расчет и построение графиков произведены с помощью программы Ikura. 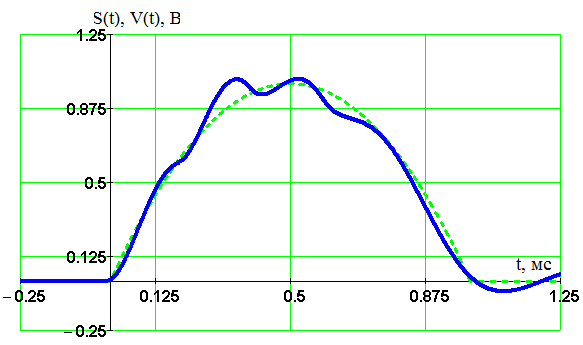 Рисунок 17 – Исходный непрерывный (штриховая линия) и восстановленный (непрерывная линия) с погрешностью d=0.63% сигналы. 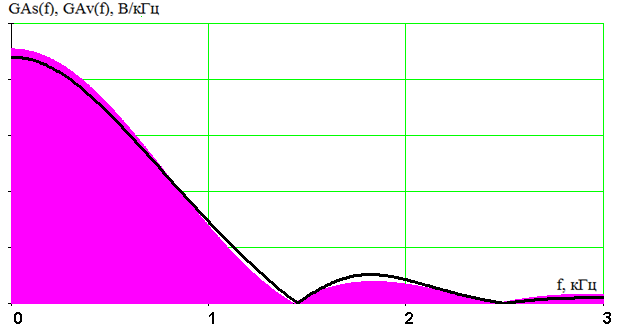 Рисунок 18 – Спектральные плотности амплитуд исходного (область, залитая цветом) и восстановленного с погрешностью d=0.63% сигналов С увеличением частоты дискретизации до пяти килогерц число отсчетных импульсов возросло до значения N=6. Это соответствует уменьшению погрешности восстановления. С частотных позиций увеличение частоты дискретизации соответствует отдалению копий спектра исходного сигнала в спектре дискретизированного сигнала и, соответственно уменьшению их взаимного влияния и влияния на нулевую копию. Значит, погрешность восстановления уменьшается. Восстановленный сигнал все больше приближается к исходному непрерывному сигналу (рисунок 17). Также их частотные характеристики сближаются (рисунок 18). Качество восстановления сигнала зависит также от формы АЧХ восстанавливающего фильтра. Для исследования этой зависимости заменим заданный фильтр нижних частот на идеальный, обладающей прямоугольной АЧХ, равномерной в полосе пропускания и обнуляющейся на частоте среза. Заранее можно предположить, что погрешность восстановления уменьшится, так как из-за отсутствия переходной области фильтр не будет выделять соседние копии спектра исходного непрерывного сигнала. Ход исследований аналогичен изложенному в пункте 5. В связи с этим опустим подробное описание построения графиков и проведения расчетов. Отметим только, что теперь импульсная характеристика существует во все моменты времени имеет вид: Зависимость погрешности восстановления от частот среза и дискретизации изображена на рисунке 19 и продублирована таблицей 2. 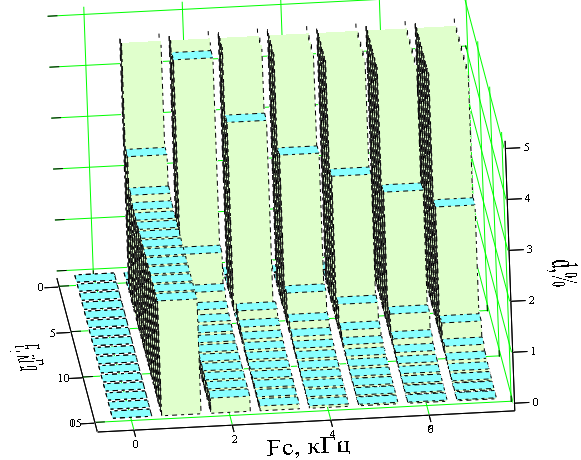 Рисунок 19 – Зависимость погрешности восстановления от частот дискретизации и среза идеального восстанавливающего фильтра Таблица 2 – Погрешность восстановления как функция частот среза идеального фильтра и дискретизации
Как видно из рисунка 19 и таблицы 2 при тех же частотах погрешность восстановления стала меньше и равной d=0.584 %. На рисунке 20 изображены временные диаграммы исходного непрерывного сигнала (пунктирная линия), а также сигналов на выходе реального (штриховая линия) и идеального (сплошная линия) фильтров нижних частот. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
