Курсовая 3318113. 1 Спектральный анализ дискретизируемого сигнала
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Введение В настоящее время широко распространена дискретная и цифровая техника, которая обрабатывает дискретизированные сигналы. Дискретизация радиосигналов проводится в соответствии с теоремой Котельникова и заключается в представлении исходного непрерывного сигнала в виде последовательности отсчетов. Восстановление дискретизированных сигналов возможно также с использованием теоремы Котельникова. Из-за неограниченности спектров сигналов копии спектра дискретизированного сигнала будут перекрываться между собой, что неизбежно приведет к возникновению погрешности восстановления. Также погрешность будет возникать из-за нелинейности частотной характеристики восстанавливающего фильтра в полосе пропускания, ненулевой длительности отсчетных импульсов, а также конечного затухания за пределами полосы пропускания фильтра. Целью данной курсовой работы является дискретизация заданного видеосигнала, последующее восстановление его с использованием реального фильтра, а также исследование влияния частоты дискретизации сигнала и частоты среза фильтра на качество восстановления. В соответствии с полученными зависимостями необходимо произвести выбор оптимальных значений частот для обеспечения требуемой погрешности восстановления. В данной курсовой работе для проверки правильности расчетов, а также исследование влияния частоты дискретизации и частоты среза восстанавливающего фильтра на погрешность восстановления и выбор параметров системы дискретной передачи сигналов, была использования программа Ikura. Построение графиков проводилось с использованием пакета Mathsoft MathCAD Professional 2014. Имитационное моделирование проводилось с использованием программы Electronics WorkBench 5.12. 1 Спектральный анализ дискретизируемого сигнала Исходный непрерывный сигнал представлен выражением: 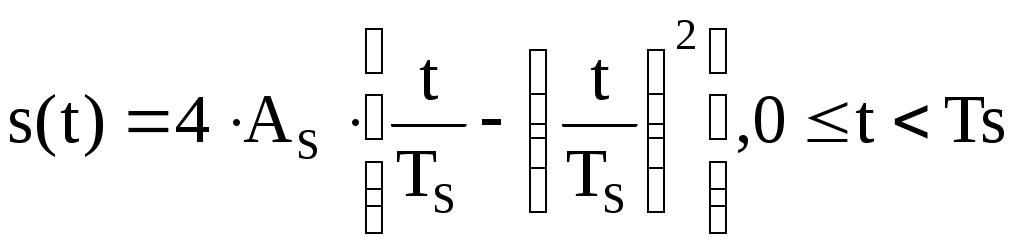 , (1) , (1)где амплитуда и длительность сигнала, соответственно равны As = 1 В, Ts = 1 мс. Временная диаграмма сигнала представлена на рисунке 1. 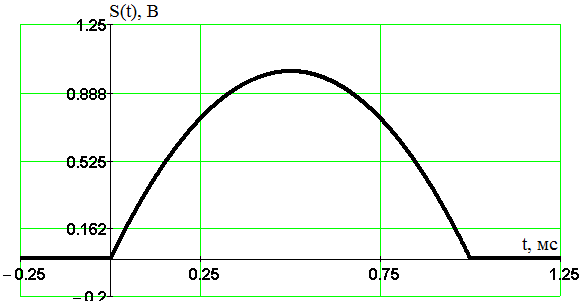 Рисунок 1 - Временная диаграмма исходного непрерывного сигнала. Как видно из рисунка 1 исходный сигнал является непериодическим, а поскольку он имеет четкие границы в точках t=0 и t=TS, то его энергия будет конечной, следовательно, в частотной области заданный сигнал будет описываться своей комплексной спектральной плотностью(КСП) - КСП непериодического сигнала с ограниченной энергией рассчитывается путем применения прямого преобразования Фурье к его временному описанию: Однако, можно использовать и другой подход, основанный на применений теорем о спектрах, который упрощает расчеты. Процесс вычисления спектра представлен в приложении А. В результате расчетов получили следующие выражения 3 и 4, которые представляют собой действительную и мнимую части комплексной спектральной плотности исходного непрерывного сигнала, как функции циклической частоты – 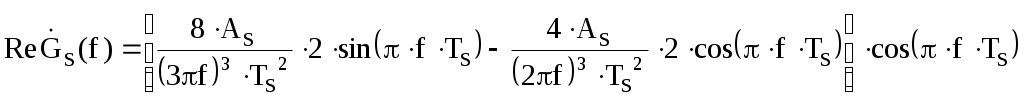 (3) (3)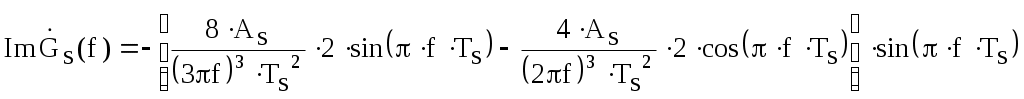 (4) (4)Тогда выражения для спектральной плотности амплитуд и спектра фаз сигнала определяются соответственно по формулам (5) и (6): 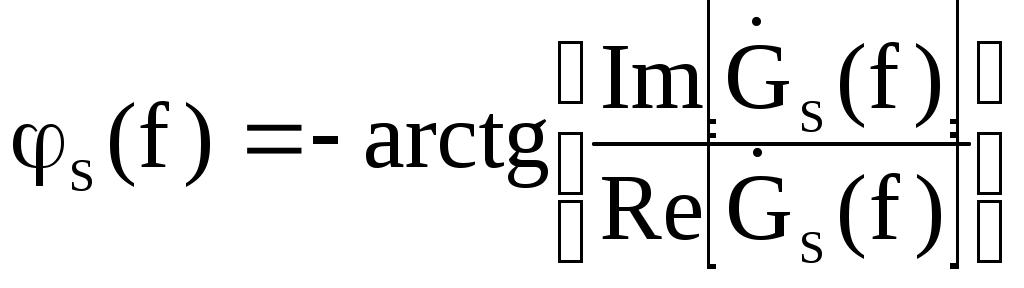 (6) (6)Графически эти характеристики изображены ниже на рисунках 2 и 3. Точками показаны результаты численного расчета с помощью MathCad в виде зависимостей Gsh(f) и φsh(f). 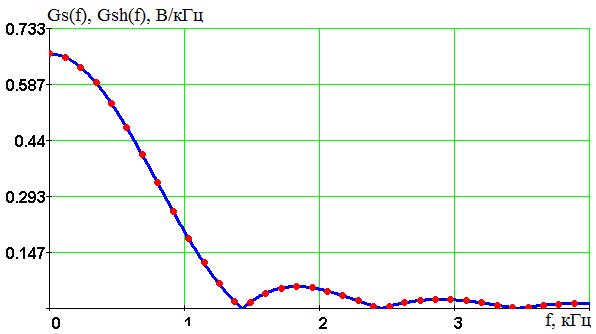 Рисунок 2 - Спектр амплитуд дискретизируемого сигнала 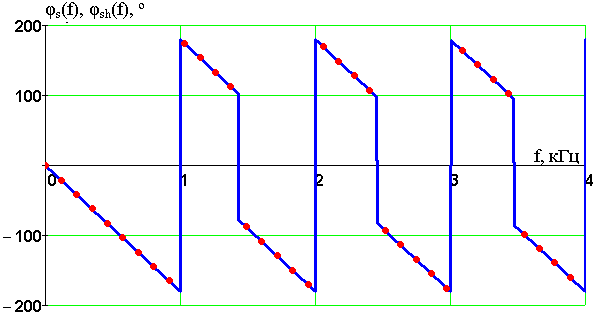 Рисунок 3 - Спектр фаз дискретизируемого сигнала Как видно из полученных зависимостей, спектральная плотность амплитуд исходного непрерывного сигнала является бесконечным, это говорит том, что его невозможно будет восстановить, в соответствии с теоремой Котельникова, без погрешности. Наиболее значимой областью спектра, на долю которой приходится большая часть энергии, сосредоточена в полосе частот до 1,5 кГц, если смотреть на рисунок 2. Определим более точно значение практической ширины спектра, используя энергетический критерий, как частоту, ограничивающую справа область значений КСП, в пределах которой сосредоточено девяносто пять процентов энергии сигнала. Для этого нужно использовать равенство Парсеваля: В выражении (7) q=0.95 – доля энергии, приходящаяся на искомую область частот, Es - энергия сигнала. В соответствии с расчетом, приведенным в приложении А, энергия сигнала получилась равной E = 0.53 В2 Таким образом, цель данного этапа достигнута – найдена предварительная частота дискретизации и можно переходить к следующему этапу работы. 2 Расчет характеристик сигнала на выходе дискретизатора Дискретизированный сигнал представляет собой последовательность отсчетных импульсов, отстоящих друг от друга на время, равное периоду дискретизации. Число импульсов определяется в соответствии с формулой: N=floot где T – период дискретизации сигнала, равный Как следует из формулы (9), число отсчетных импульсов для данного периода получается равным N=3. Сигнал на выходе дискретизатора определяется выражением: Рассчитав значения сигнала в отсчетные моменты времени, получим следующее выражение, определяющее сигнал на выходе дискретизатора. На рисунке 4 изображен дискретизированный сигнал, для наглядности представленный совокупностью отсчетных импульсов ненулевой длительности. Штриховой линией представлен исходный непрерывный сигнал – s(t). 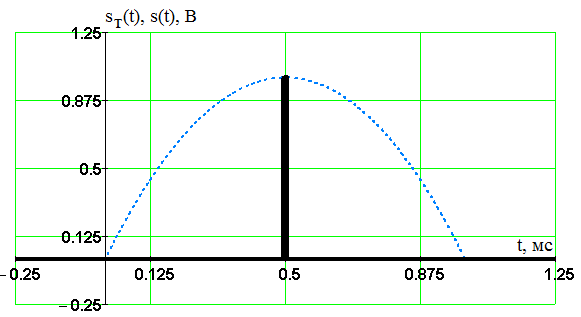 Рисунок 4 - Временная диаграмма дискретизированного сигнала Рассчитаем комплексную спектральную плотность дискретизированного сигнала численно, используя формулу: Модуль и аргумент этого выражения определяют, соответственно, комплексную спектральную плотность амплитуд и спектр фаз дискретизированного сигнала. Графики спектральной плотности амплитуд и спектра фаз представлены на рисунках 5 и 6. 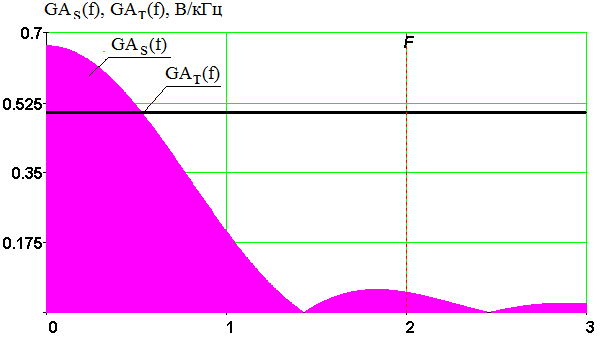 Рисунок 5 – Спектральные плотности амплитуд исходного – GAS(f) и дискретизированного – GAT(f) сигналов 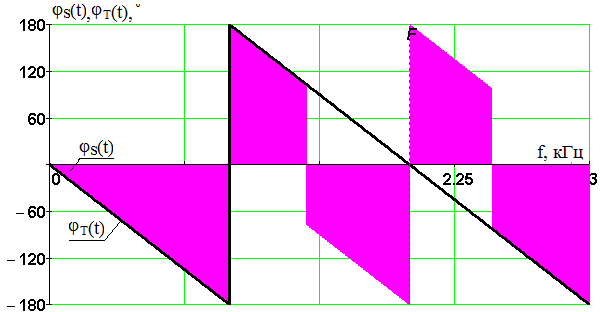 Рисунок 6 – Спектры фаз исходного – φS(f) и дискретизированного – φT(f) сигналов Рисунки 5 и 6 говорят о том, что уже на этапе дискретизации спектры исходного непрерывного и дискретизированного сигналов отличаются. Причиной этому служит неограниченность частотного спектра непрерывного сигнала, следствием чего является перекрытие копий частотных полос в составе спектра дискретизированного сигнала. Из-за этого искажается форма нулевой копии частотной полосы, которая представляет собой спектр восстановленного сигнала. Исказив спектр, мы неизбежно придем к тому, что восстановленный сигнал будет отличаться от исходного. Причем отличие этих сигналов будет тем меньше, чем меньше перекрываются копии частотных полос, то есть, чем больше частота дискретизации. Определяем, предварительно, что полоса пропускания восстанавливающего фильтра должна быть равной FC=1 кГц, так как она является границей нулевой копии частотной полосы, которую следует выделять. 3 Анализ частотных и временных характеристик восстанавливающего фильтра По условию технического задания, необходимо проанализировать фильтр с полюсами передаточной функции 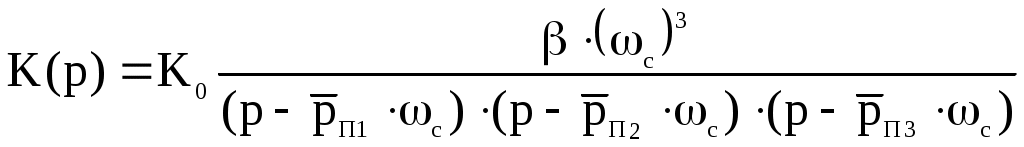 (12) (12)Подставив в это выражение значения полюсов и заменив p на j 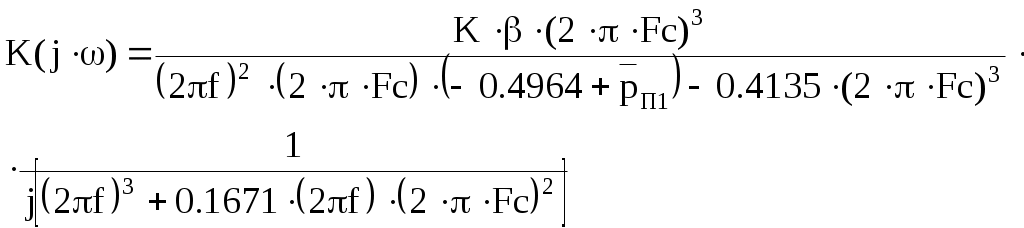 (13) (13) Из выражения для комплексного коэффициента передачи получим АЧХ и ФЧХ восстанавливающего фильтра и выразим их как функции циклической частоты: 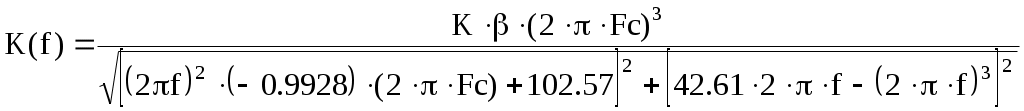 (14) (14)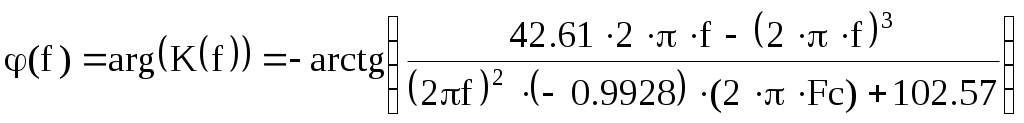 (15) (15)Подробный расчет комплексного коэффициента передачи приведен в приложении А. АЧХ и ФЧХ восстанавливающего фильтра представлены на рисунках 7 и 8 соответственно. Точками показаны результаты численного расчета в Mathcad. 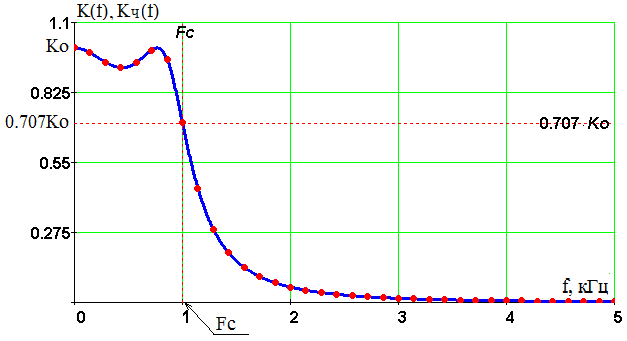 Рисунок 7 - АЧХ восстанавливающего фильтра 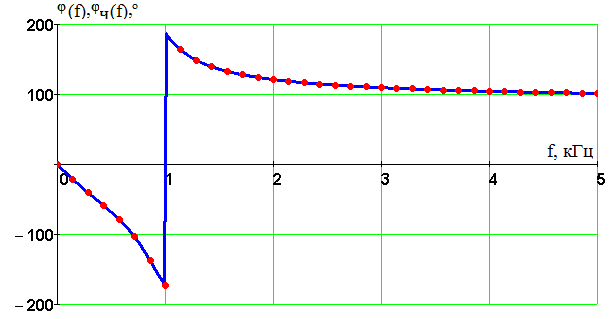 Рисунок 8 - ФЧХ восстанавливающего фильтра Рисунки 7 и 8 демонстрируют отличие частотных характеристик заданного фильтра от идеальных. АЧХ является неравномерной, а ФЧХ – нелинейной. Это означает, что спектральные составляющие разных частот будут попадать на выход с разными коэффициентом усиления и приращением по фазе. То есть сигнал, проходя через фильтр, будет искажаться. К тому же, как показывает рисунок 7, АЧХ фильтра вне полосы пропускания не равна нулю, следовательно, на выход будут попадать ненужные спектральные составляющие высших копий частотных полос спектра исходного непрерывного сигнала, внося дополнительные искажения в спектр восстановленного сигнала. Рассмотрим фильтр с временных позиций, проанализировав его инерционные свойства и импульсную характеристику. Поскольку ФЧХ нелинейная, то время задержки фильтром сигнала будет зависеть от частоты. 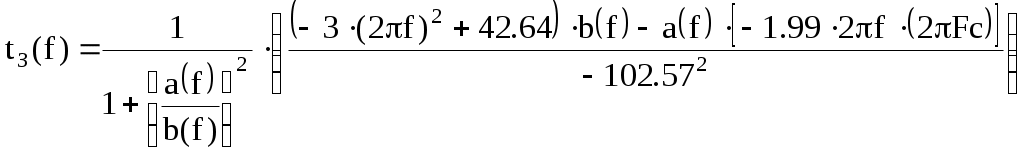 (16) (16)где Расчет времени задержки сигнала приведен в приложении А. График получившейся зависимости показан на рисунке 9. 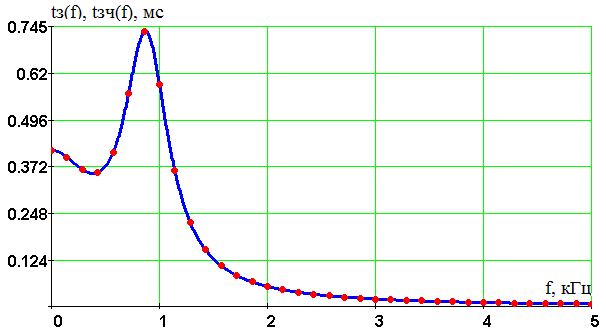 Рисунок 4 - Зависимость времени задержки сигнала от частоты Время задержки на нулевой частоте равно tЗ= 0.42 мс. Рассчитаем импульсную характеристику фильтра по формуле: 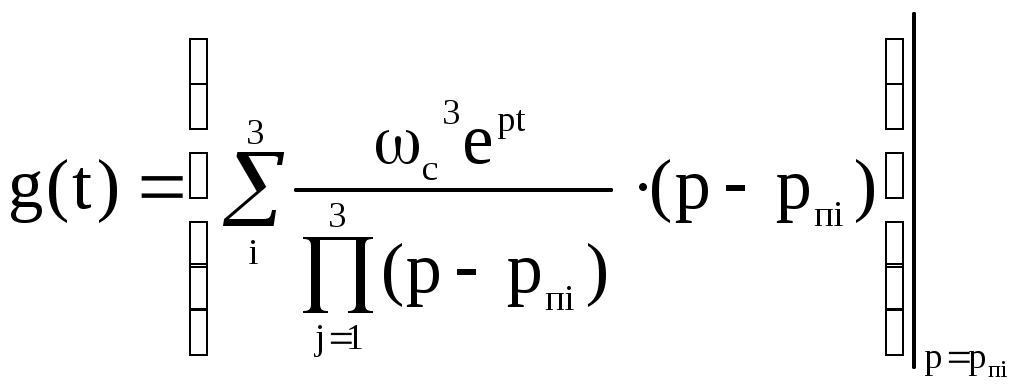 (17) (17)В результате расчета получили следующее выражение: 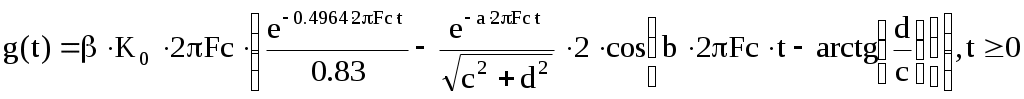 (18) (18)где a = -0.2482; b = 0.8783; c = -1.54; d = 0.44. Расчет полностью приведен в приложении А. График получившейся импульсной характеристики отображен на рисунке 10. 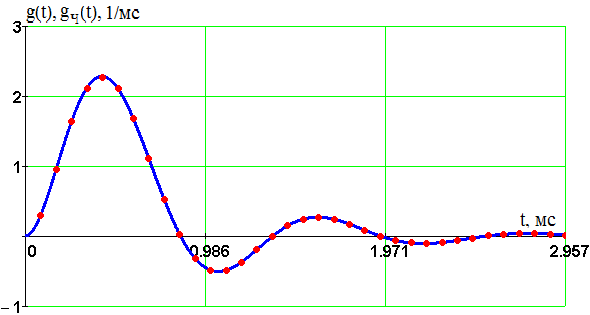 Рисунок 50 - Импульсная характеристика восстанавливающего фильтра Рисунки 9 и 10 демонстрируют несоответствие временных характеристик реального фильтра характеристикам идеального. У заданного фильтра время задержки зависит от частоты (рисунок 9), а это значит, что разные спектральные составляющие придут на выход через разные промежутки времени, что исказит выходной сигнал. Импульсная характеристика фильтра существует только в положительные моменты времени (рисунок 10), что приводит к проявлению эффекта Гиббса в АЧХ цепи, искажая её форму. На рисунке 14 изображены совместно график АЧХ используемого фильтра – K(f) (штриховая линия) и амплитудные спектры исходного – GAs(f) (область, залитая цветом) и дискретизированного – GAт(f) (сплошная линия) сигналов. 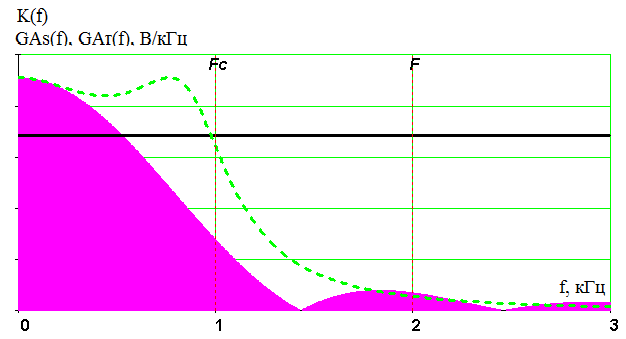 Рисунок 11 - Частотные характеристики исходного и дискретизированного сигналов и восстанавливающего фильтра нижних частот Таким образом, все выше перечисленные выводы говорят о том, что мы никогда точно восстановить сигнал не сможем. Ни дискретизатор, ни фильтр не удовлетворяют требованиям теоремы Котельникова, сформулированным для абсолютно точного восстановления сигнала. 4 Расчет сигнала, восстановленного по дискретным отсчетам Непрерывный сигнал на выходе восстанавливающего фильтра V(t) определяется выражением: Графики исходного непрерывного (штриховая линия) и восстановленного по дискретным отсчетам с помощью фильтра, представлены на рисунке 12. 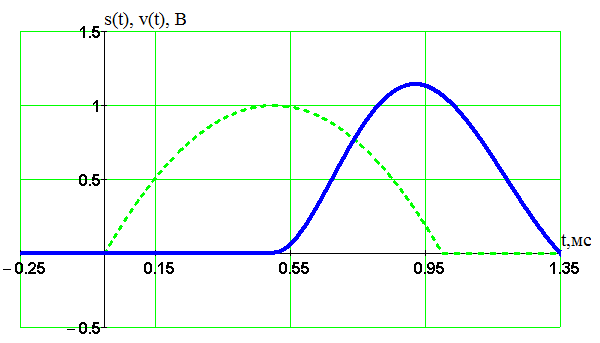 Рисунок 6 - Исходный и восстановленный сигналы Как видим, после прохождения через реальный фильтр сигнал запоздал во времени из-за его инерционности, а также исказил свою форму из-за ряда факторов, перечисленных в предыдущем пункте. Запаздывание сигнала не есть его искажения, а поэтому качество восстановления следует искать в различиях форм исходного и восстановленного сигналов. Уберем запаздывание сигнала, сдвинув его влево на время, равное tз = 0.42 мс, а также выровняем масштабы исходного и восстановленного сигналов, умножив последний на коэффициент μ. Результаты этого преобразования представлены на рисунке 13. 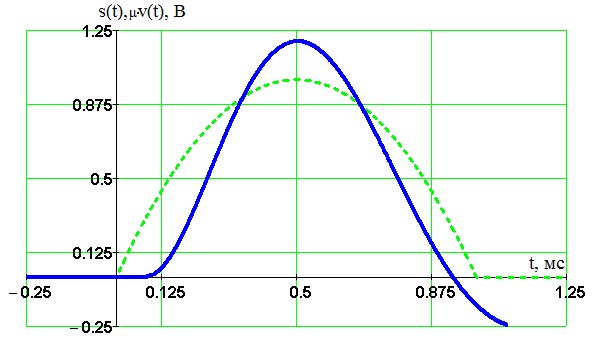 Рисунок 7 - Восстановленный сигнал (сплошная линия) на фоне исходного (штриховая линия) Как видно из рисунка 13, исходный и восстановленные сигналы, как и предполагалось, различаются по форме. Это происходит, как было выше сказано, из-за невозможности удовлетворения на практике условиям теоремы Котельникова, соответствующим абсолютно точному восстановлению сигнала по дискретным отсчетам. Спектры амплитуд и фаз восстановленного сигнала на фоне исходного (области, залитые цветом) представлены, соответственно, на рисунках 14 и 15. 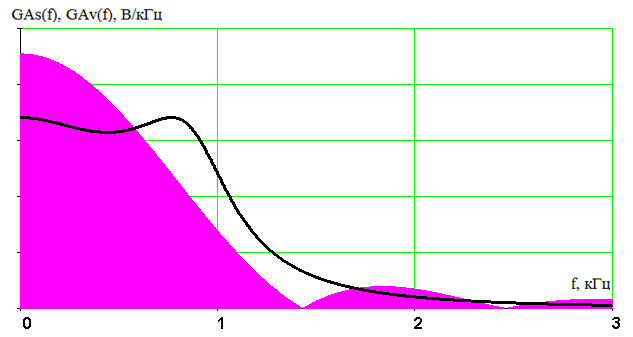 Рисунок 8 – Спектральная плотность амплитуд исходного (область, залитая цветом) и восстановленного (сплошная линия) сигналов 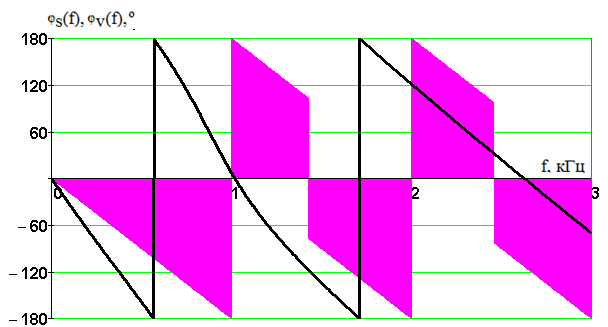 Рисунок 9 - Спектры фаз исходного (область, залитая цветом) и восстановленного (сплошная линия) сигналов Рисунки 14 и 15 показывают несоответствие частотных характеристик исходного и восстановленного сигналов из-за изначального искажения спектра на этапе дискретизации, к которому добавляется погрешность фильтрации из-за несоответствия частотных характеристик восстанавливающего фильтра характеристикам идеального. Для более детальной оценки качества восстановления рассчитаем погрешность восстановления по формуле: |
