Главная страница
Навигация по странице:

  • Контрольная работа №1.

  • Математическое описание заданного периодического сигнала.

  • Анализ временных свойств сигнала и формулировка обоснованных предложений о свойствах и особенностях спектрального состава сигнала.

  • Вычисление спектров амплитуд и фаз. Характер огибающей спектра амплитуд.

  • Построение оценки сигнала

  • Расчет относительного значения квадрата среднеквадратической погрешности представления сигнала оценкой из трех гармонических колебаний.

  • Определение комплексной спектральной плотности непериодического сигнала. Совпадающего с заданным периодическим на протяжении одного периода в симметричных пределах (- T /2, T

  • /2) и равного нулю при других временах .

  • Сопоставление спектров периодического и не периодического сигналов.

  • Определение энергии и средней мощности заданного сигнала на участке цепи с сопротивлением 1 Ом. Э=

    		•

    Лабораторная по РТЦиС. 1-11_РТЦ и С. Контрольная работа 1. Спектральный анализ периодических и непериодических управляющих сигналов. Вариант 11


    Скачать 1.23 Mb.
    НазваниеКонтрольная работа 1. Спектральный анализ периодических и непериодических управляющих сигналов. Вариант 11
    АнкорЛабораторная по РТЦиС
    Дата04.11.2022
    Размер1.23 Mb.
    Формат файлаdoc
    Имя файла1-11_РТЦ и С.doc
    ТипКонтрольная работа
    #770602




    Министерство образования Российской Федерации
    ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

    Кафедра радиоэлектроники и защиты информации (РЗИ)
    РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ. Ч-1.
    Контрольная работа №1. Спектральный анализ периодических и

    непериодических управляющих сигналов.

    Вариант № 11.


    Выполнил:

    Студент гр. ########

    alexsys

    Код доступа ##########

    Пароль######39


    2004.

    Все вычисления проводились в программе MathCAD 2000.

    Исходные данные: (параметры видеосигнала, изображенного на рисунке 1.)


    • Период сигнала Т=8*0,1 млс;

    • Длительность импульса =0,1 млс;

    • Амплитуда импульса Е=3,2 В;

    • Временные свойства сигнала:

    нечетная симметрия относительно t=0.

    Функция общего вида относительно t=T/4




    1. Математическое описание заданного периодического сигнала.


    Периодический сигнал представляет собой знакочередующуюся последовательность импульсов прямоугольной формы. Математическое описание проведем, используя графическую модель сигнала, изображенную на рисунке 1.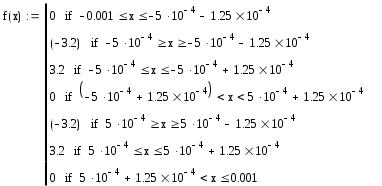



    T=0.001
    Скважность, определяемая отношением периода сигнала к длительности

    прямоугольного импульса.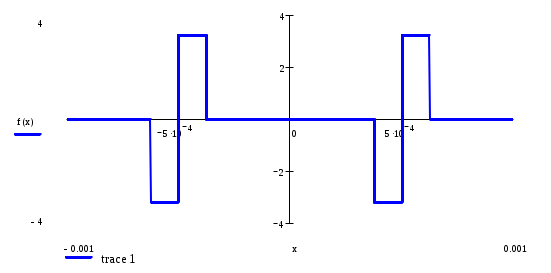




    Рисунок 1.—Временное представление сигнала



    1. Анализ временных свойств сигнала и формулировка обоснованных предложений о свойствах и особенностях спектрального состава сигнала.


    Анализируя временное представление сигнала, получим:

    1) - сигнал является нечетной функцией времени.

    2) Сигнал знакочередующийся. И в этом случае постоянная

    составляющая равна нулю.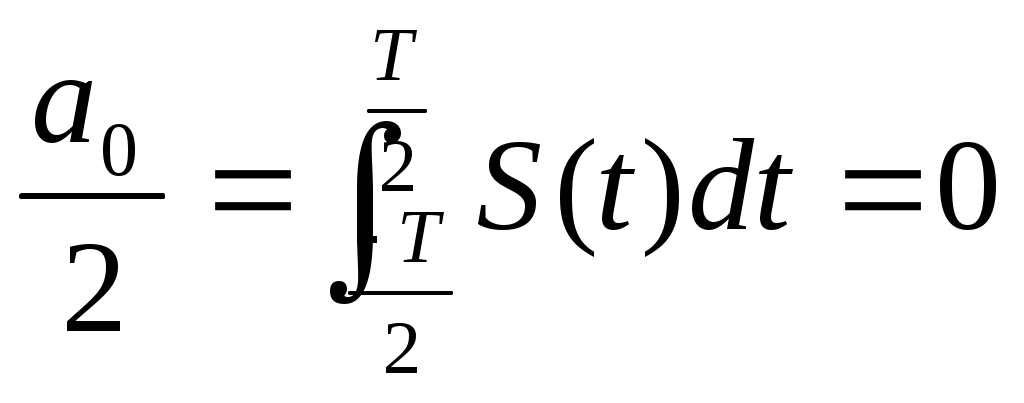


    На основании этого предположим, что в разложении сигнала будут присутствовать

    синусоидальные элементарные гармонические составляющие, то есть

    Ряд Фурье преобразуем следующим образом: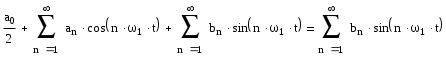



    1. Вычисление спектров амплитуд и фаз. Характер огибающей спектра амплитуд.


    Проведем расчет коэффициентов , используя при этом формулу из таб.2.3

    учебного пособия для нечетной функции.

    Исходя из графической модели сигнала, произведем вычисления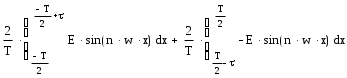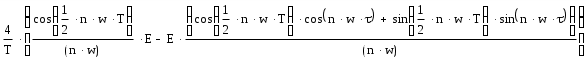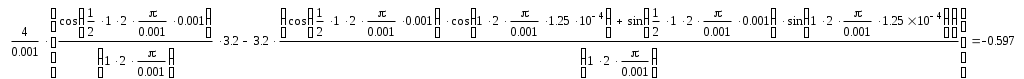
    T=0,001
    =


    =


    Систематизируем полученные результаты: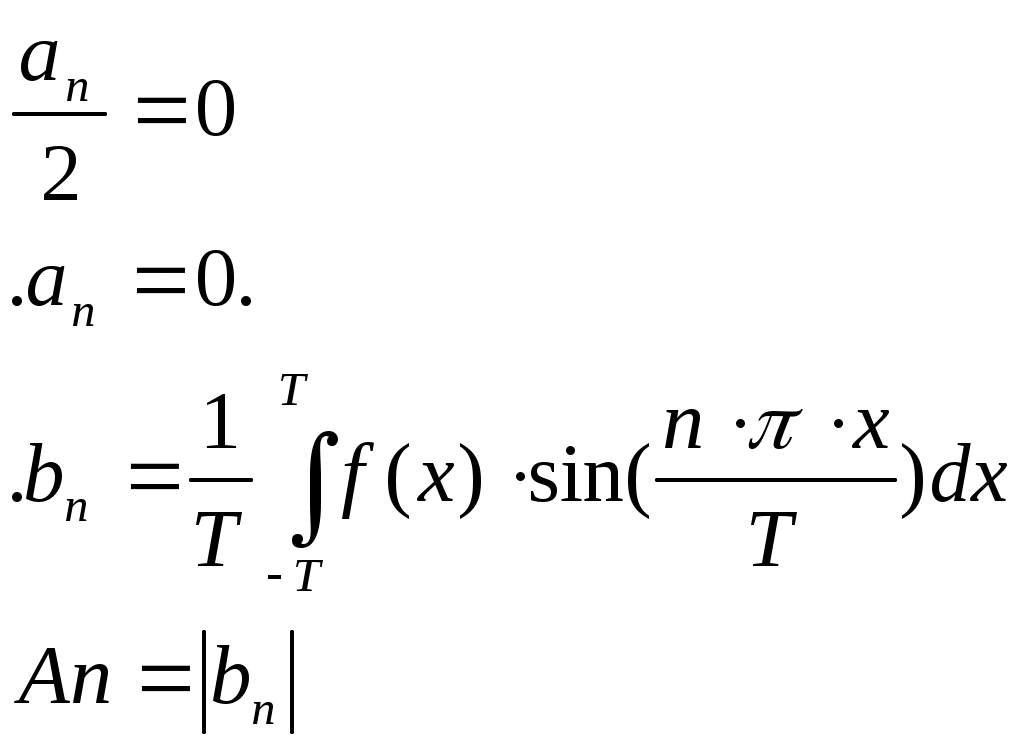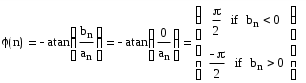



    Результаты расчетов. Таблица 1.

    n
    0
    1
    2
    3
    4
    5
    6
    7
    8
    9

    an
    a0/2=0
    0
    0
    0
    0
    0
    0
    0
    0
    0

    bn
    0
    -0,597
    1,019
    -1,159
    1,019
    -0,696
    0,34
    -0,085
    0
    -0,066

    An
    a0/2=0
    0,597
    1,019
    1,159
    1,019
    0,696
    0,34
    0,085
    0
    0,066

    φn
    0
    π/2
    - π/2
    π/2
    - π/2
    π/2
    - π/2
    π/2
    - π/2
    π/2




    1. Построение оценки сигнала


    Произведем восстановление сигнала по его спектру




    Спектр коэффициентов b(n)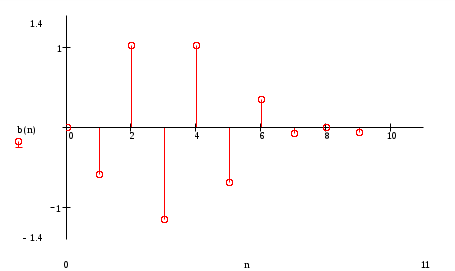


    Спектр амплитуд А(n)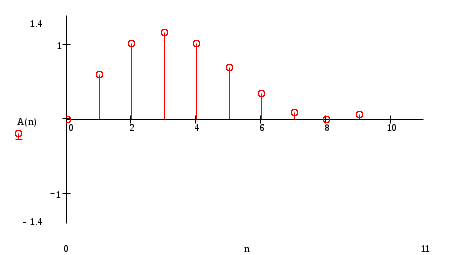



    Спектр фаз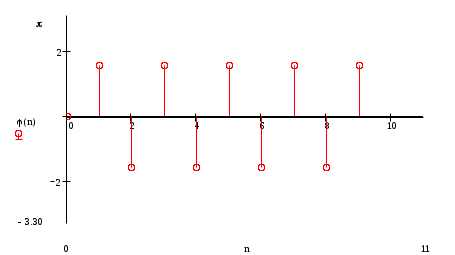


    Спектр коэффициентов, С(n)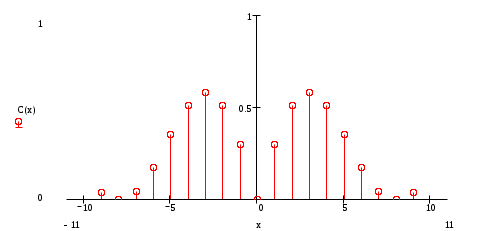



    Спектр коэффициентов, ф(n)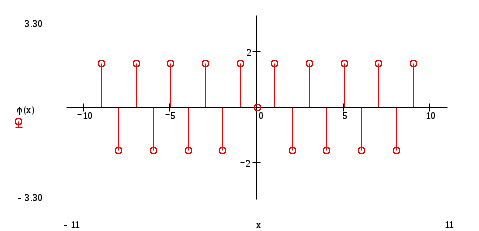




    При n=3, получим

    S3(t)= - 0,597*cosw1t+1,019*cos2w1t+(- 1,159)*cos3w1t
    w1= - угловая частота.

    В соответствии с последней формулой производим расчет компонент оценки и их

    суммы.
    Таблица 2. Поведение оценки в интервале (0,T/2)


    t

    0
















    -0,597*cosw1t
    -0,597
    -0,457
    -0,561
    0,41
    -0,588
    0,429
    0,236
    0,561
    0

    1,019*cos2w1t
    1,019
    0,78
    0,957
    -0,7
    1,003
    -0,733
    -0,403
    -0,958
    0

    -1,159*cos3w1t
    -1,159
    -0,887
    -1,089
    0,796
    -1,141
    0,834
    0,459
    1,089
    0

    S3(t)
    -0,737
    -0,564
    -0,693
    0,506
    -0,726
    0,53
    0,292
    0,692
    0


    График оценки сигнала для трех гармонических колебаний.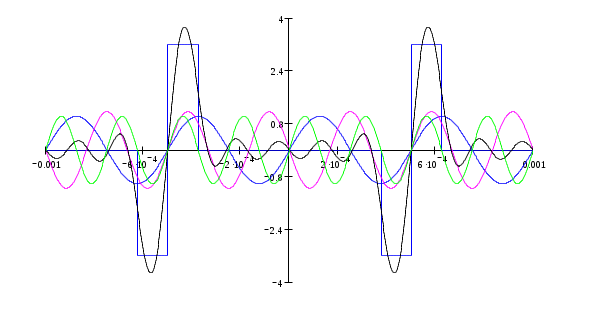








    Рис. 2. –Оценка сигнала из трех гармонических колебаний.



    1. Расчет относительного значения квадрата среднеквадратической

    погрешности представления сигнала оценкой из трех

    гармонических колебаний.
    Если s(t) представляет собой напряжение или ток, тогда квадрат сигнала численно равен мгновенной мощности p(t), рассеиваемой на сопротивление нагрузки 1 Ом.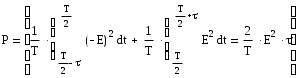


    =

    Определим среднюю мощность n-го гармонического сигнала.


    Уравнение погрешности имеет вид



    где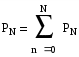


    Таблица 3. Результаты расчета погрешности



    n
    0
    1
    2
    3
    4
    5
    6
    7
    8
    9

    An, B
    0
    0,597
    1,019
    1,159
    1,019
    0,696
    0,34
    0,085
    0
    0,066

    Pn, Bт
    0
    0,178
    0,519
    0,672
    0,519
    0,242
    0,058
    3,613E-3
    0
    2,178E-3

    PN, Bт
    0
    0,178
    0,697
    1,369
    1,888
    2,13
    2,188
    2,191
    2,191
    2,193

    , %
    100
    93
    72,8
    46,5
    26,3
    17,2
    14,5
    14,4
    14,4
    14,3


    График зависимости величины погрешности от количества слагаемых ряда Фурье.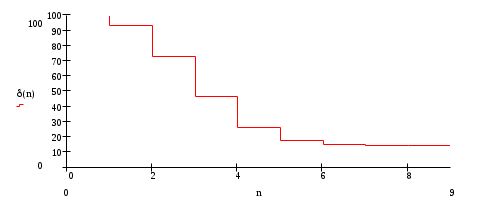



    1. Определение комплексной спектральной плотности непериодического сигнала. Совпадающего с заданным периодическим на протяжении одного периода в симметричных пределах (-T/2, T/2) и равного нулю при других временах.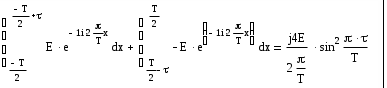




    1. Полученная спектральная плотность является мнимой функцией частоты,

    т.к. действительная равна нулю.
    2. Структура сигнала такова, что суммарная площадь под его временным

    графиком равна нулю.

    3. Размерность


    1. Построение графика модуля спектральной плотности и фазового спектра непериодического сигнала.



    Запишем выражение спектральной плотности для построения графика.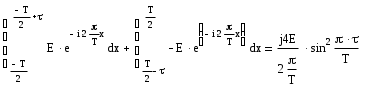

    Анализируя последнее выражение с учетом sin(nп)=0 для n=0,1,2,3….,

    получаем точки, в которых график функции S(w) пересекает частотную ось,

    Результаты расчетов запишем в таблицу 4.

    ωτ/π


    SA(w)

    0,5
    1,019
    1,019

    1
    0,509
    1,018

    1,5
    0,34
    0,34

    2
    0,255
    0

    2,5
    0,204
    0,204

    3
    0,169
    0,338

    3,5
    0,455
    0,455

    4
    0,127
    0

    4,5
    0,113
    0,113

    5
    0,102
    0,204

    5,5
    0,093
    0,093

    6
    0,085
    0

    6,5
    0,078
    0,078

    7
    0,073
    0,146

    7,5
    0,068
    0,068

    8
    0,064
    0


    На рисунке ниже изображена спектральная плотность исследуемого сигнала.

    АЧХ спектра и ФЧХ спектра.

    S(w)=A(w)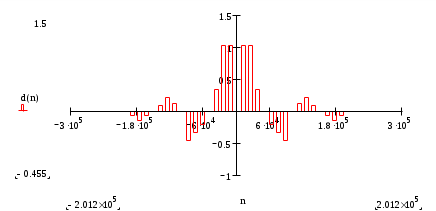


    |S(w)|=|A(w)|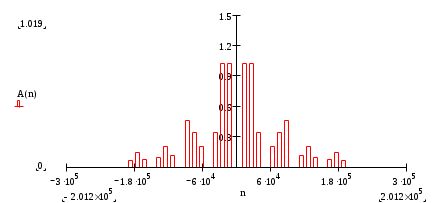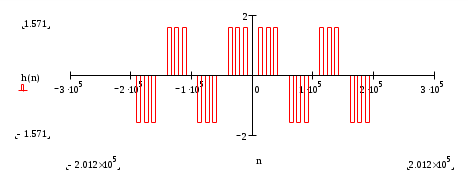






    1. Сопоставление спектров периодического и не периодического сигналов.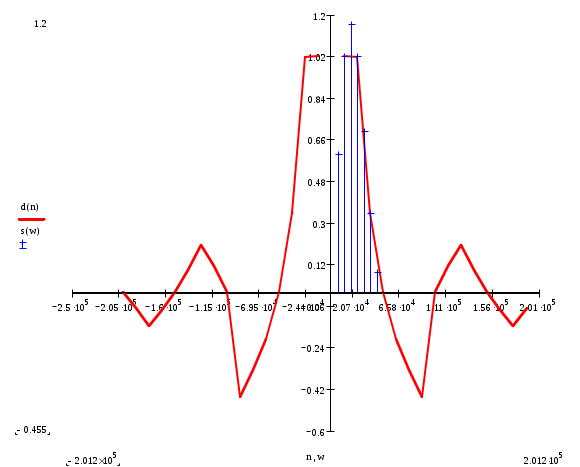




    Рис. 3. Сравнение спектров периодического и непериодического сигналов.
    Сравнение спектров периодического и непериодического сигналов показывают, что гармоники, построенные на частотах, кратных w1 и ограниченные спектральной плотностью непериодического сигнала, совпадают со значениями Сn на спектральных диаграммах периодического сигнала.


    1. Определение энергии и средней мощности заданного сигнала на участке цепи с сопротивлением 1 Ом.

    Э=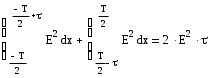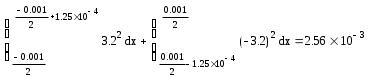




    Тогда согласно данным c и средняя мощность равна
    Bт.

    10. Выводы

    В настоящей работе проведено исследование спектральных свойств двух сигналов - периодического и непериодического. Периодический сигнал представляет собой знакочередующуюся последовательность импульсов прямоугольной формы.

    Сигнал описывается аналоговой функцией времени с двумя видами симметрии

    Нечетная симметрия относительно t=0.

    Функция общего вида относительно t=T/4


    Эти особенности временных свойств сигнала определяют характер его спектра:

    1. Спектр периодического сигнала дискретный, полностью характеризуется рядом Фурье.

    2. Нечетность функции, описывающей сигнал, определяет наличие только синусоидальных составляющих.

    3. Наличие разрывов в функции приводит к достаточно медленной сходимости ряда Фурье.

    Особенностью исследуемого непериодического сигнала является наличие в его составе импульсов различной длительности.

    Кроме того на интервале(-T/2,T/2) он полностью совпадает с непериодическим

    сигналом, исследованным в начале работы.

    Могут быть выделены следующие особенности спектра непериодического сигнала:

    1. Спектр непериодического сигнала сплошной, полностью характеризуется комплексной спектральной плотностью.

    2. Нечетность сигнала во времени определяет мнимый характер спектральной плотности.

    3. Спектральная плотность равна нулю на нулевой частоте вследствие нулевого среднего значения сигнала.

    4. Ограниченность сигнала во времени определяет пульсирующий характер его спектра.

    5. Энергия непериодического сигнала- конечная величина. Энергия периодического сигнала бесконечна и физического смысла не имеет.

    Модуль спектральной плотности одиночного импульса и огибающей линейчатого спектра периодической последовательности, полученной путем повторения заданного импульса, совпадают по форме и отличаются только масштабом.

    написать администратору сайта