шапагат. нурбол. Содержание Задание на курсовую работу 3 Спектральный анализ непериодического сигнала. 4 Спектральный анализ периодического сигнала. 5

• Название: Содержание Задание на курсовую работу 3 Спектральный анализ непериодического сигнала. 4 Спектральный анализ периодического сигнала. 5
• Анкор: шапагат
• Дата: 11.01.2021
• Размер: 324 Kb.
• Имя файла: нурбол.doc
• Тип: Документы; #167108

Содержание:
Задание на курсовую работу 3

1. Спектральный анализ непериодического сигнала. 4

2. Спектральный анализ периодического сигнала. 5

3. Спектральный анализ одиночного радиоимпульса. 7

4. Спектральный анализ периодической последовательности

радиоимпульсов. 9

5. Корреляционный анализ непериодического сигнала. 10

6. Спектральный анализ линейной цепи. 11

Список литературы 13

Задание на курсовую работу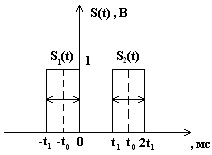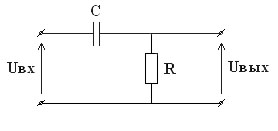





Рис. 1. Заданный сигнал Рис.2. Заданная цепь

В курсовой работе требуется:
1.Определить амплитудный спектр видеоимпульса и построить его график.

2.Определить амплитудный спектр периодической последовательности видеоимпульсов со скважностью Q=5, построить его график.

3.Определить амплитудный спектр радиоимпульса, построить его график.

4.Определить амплитудный спектр периодической последовательности радиоимпульсов, построить его график.

5.Определить автокорреляционную функцию заданного видеоимпульса, построить её график.

6.Записать выражение для спектра видеосигнала на выходе цепи заданного вида.

1. 
   Спектральный анализ непериодического сигнала.
   

Аналитическое описание заданного сигнала: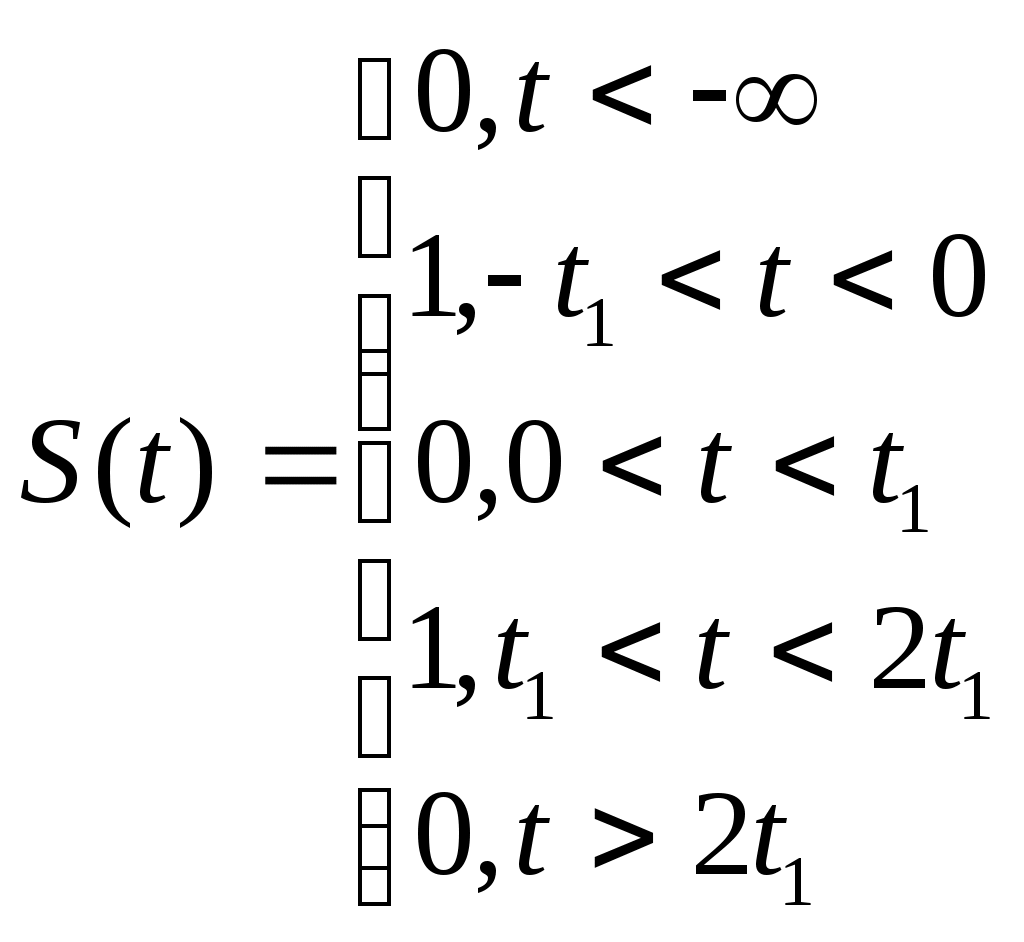

Длительность прямоугольных импульсов, составляющих сигнал:



Представим пачку заданных видеоимпульсов двумя одиночными видеоимпульсами (рис.3 а,б)
Рис.3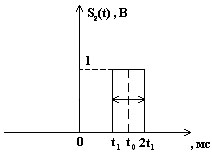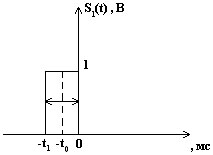



а) б)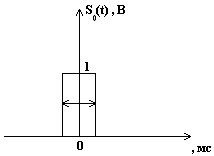
, ,

- одиночный видеоимпульс с амплитудой V₀=1В и длительностью τ_и=3мс, относительно которого рассматриваются импульсы, составляющие сигнал (рис.3 в).


в)

Таким образом, в аналитическом виде заданный сигнал (рис.1) будет иметь вид: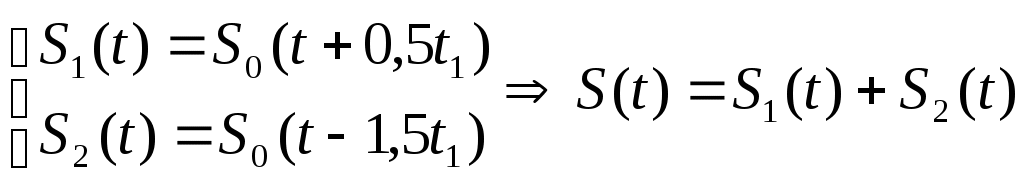



Спектральная плотность определяется преобразованием Фурье:



Функция S(ω) в общем случае является комплексной:



S(ω) – амплитудный спектр

φ(ω) – фазовый спектр
Задачу определения спектральной плотности заданного сигнала можно упростить, воспользовавшись свойствами преобразования Фурье:
, (1)

V₀ – амплитуда.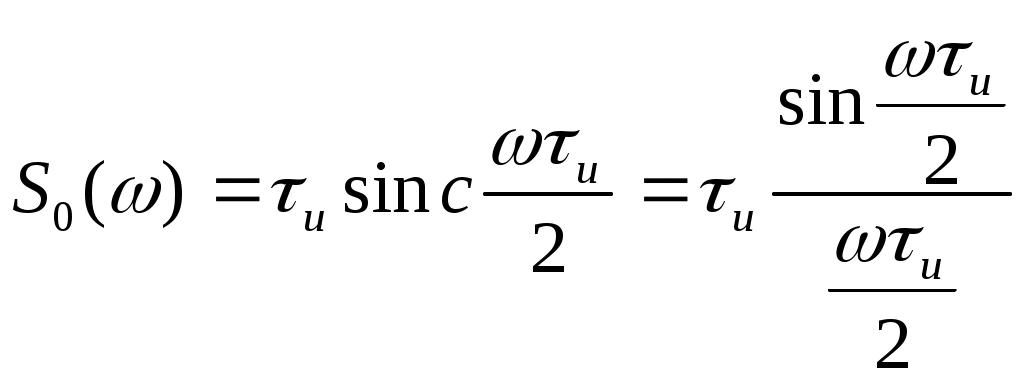

, (2) – для прямоугольного видеоимпульса

Согласно (1) и (2) получаем следующие спектральные плотности для видеоимпульсов, составляющих сигнал (τ_и=t₁ ,V₀=1):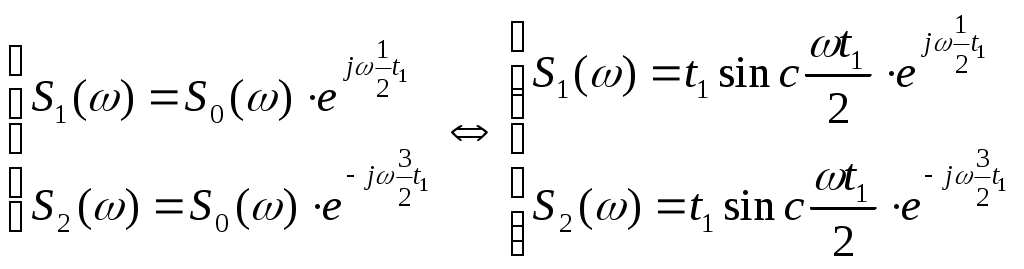



Таким образом, спектральная плотность заданного сигнала (рис.1):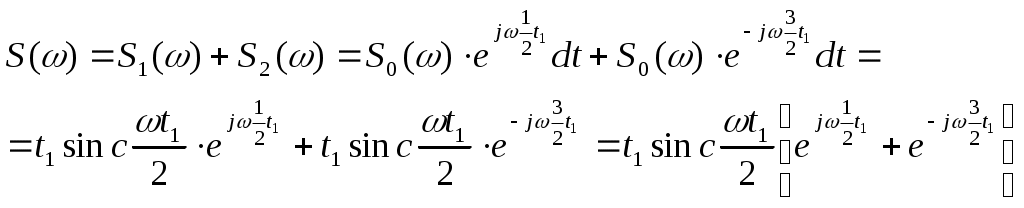


2.Спектральный анализ периодического сигнала.
Спектральный анализ периодических сигналов основан на разложении временной функции, описывающей сигнал, с периодом T и частотой ω₁=2π/T, по ортогональной системе тригонометрических функций (ряд Фурье для периодической последовательности):
, (3) ;
Совокупность амплитуд {A_n} определяет амплитудный спектр, а совокупность начальных фаз {φ_n} – фазовый спектр сигнала.

При определении амплитудного спектра периодических сигналов полезно использовать следующее равенство
, (4)
которое определяет взаимосвязь между спектрами периодических и непериодических сигналов.
Спектры периодических сигналов являются дискретными и линейчатыми, интервал дискретизации по частоте равен частоте сигнала ω₁.
Определим период T заданного сигнала получаемого периодическим повторением прямоугольного видеоимпульса (рис.) по формуле:
,
где Q=5 – заданная скважность, τ_сигн.=3τ_и= 3t₁

Аналитическое выражение для полученного сигнала: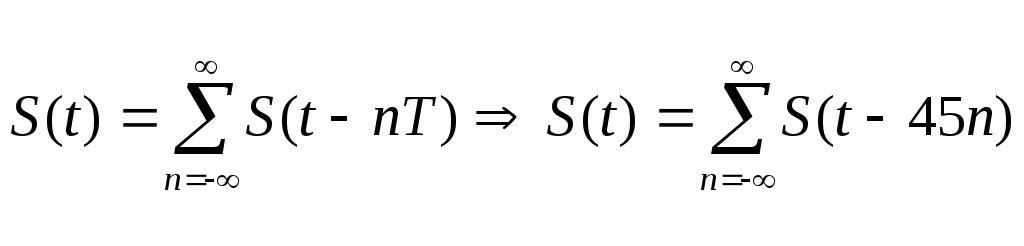

,

где S(t) – заданный сигнал
Преобразуем круговую частоту ω₁ в f1 (ω₁ [рад/с] => f₁[Гц])




f₁– интервал дискретизации по частоте.
По формуле (4) определим амплитудный спектр периодической последовательности заданного сигнала: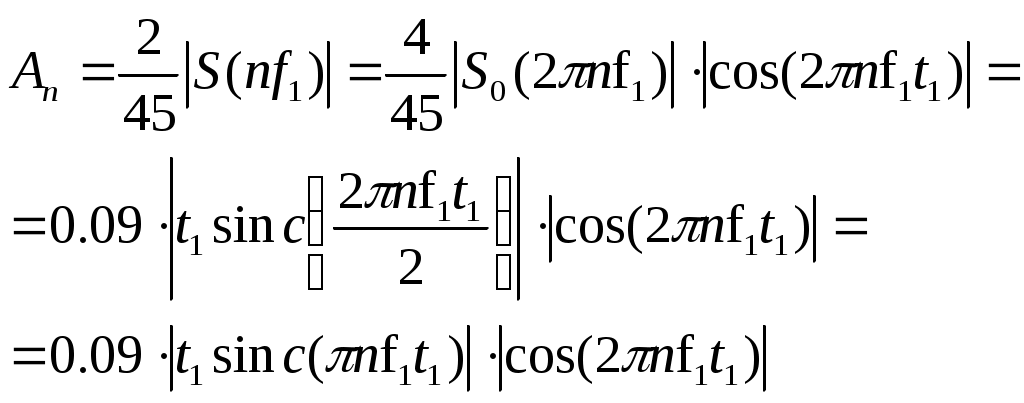

– из пункта 1 курсовой работы


Временная диаграмма периодической последовательности заданного сигнала и график её амплитудного спектра представлены на рис.6 и 7.

3. Спектральный анализ одиночного радиоимпульса
Несущая частота радиоимпульса (частота заполнения):
, ,
Определим ширину спектра Δf:

f_max– определена по графику амплитудного спектра одиночного прямоугольного видеоимпульса (рис.5), по 10% уровню от |S(f)| _max , т.е. по уровню 0.1|S(f)| _max .

К узкополосным сигналам (радиосигналам) относятся сигналы, спектры которых сосредоточены в относительно узкой по сравнению со средней частотой полосе. Узкополосный сигнал описывается выражением:
, (5)
ω₀ – частота несущего колебания

V(t), Φ(t) – амплитуда и фаза сигнала
В частном случае, когда , а V(t)=s(t) – непериодический видеосигнал, (5) описывает радиоимпульс:
, (6)
Таким образом, аналитическое выражение для полученного радиоимпульса:
,
где S(t) – заданный сигнал (см.. п.1)
Временная диаграмма одиночного радиоимпульса представлена на рис.8.


Спектральная плотность радиоимпульса определяется спектральной плотностью его огибающей: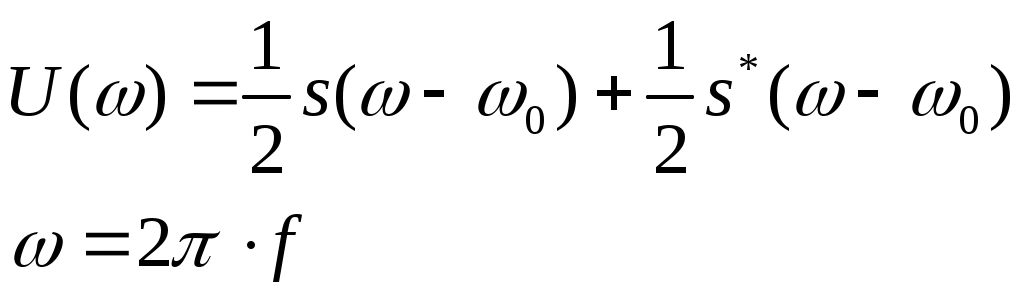



Спектр радиоимпульса U(ω) получается путём переноса спектра его огибающей S(ω) из окрестности нулевой частоты в окрестность несущей частоты ±ω₀ (с коэффициентом 1/2):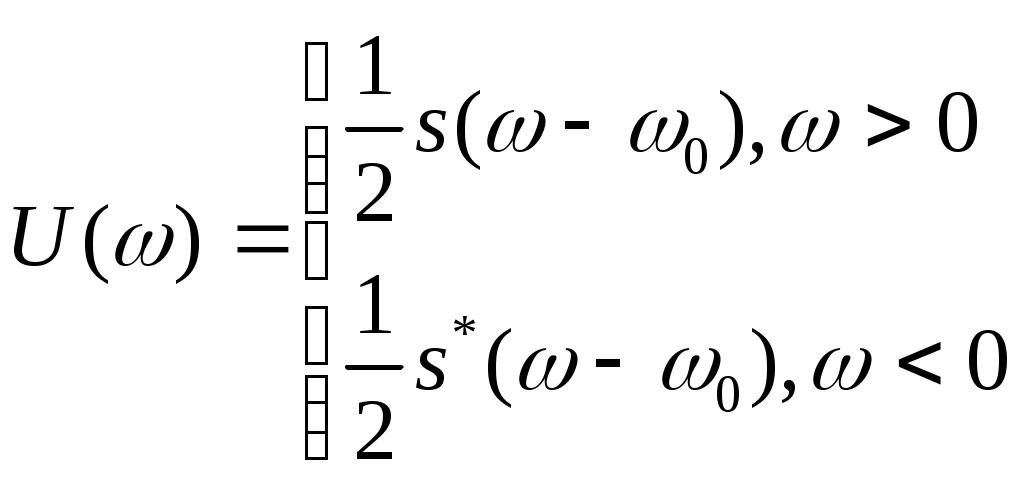

S(2π( f–f₀ )) и S(2π( f+f₀ )) – спектральные плотности видеоимпульса, составляющих заданный сигнал, определённые в п.1.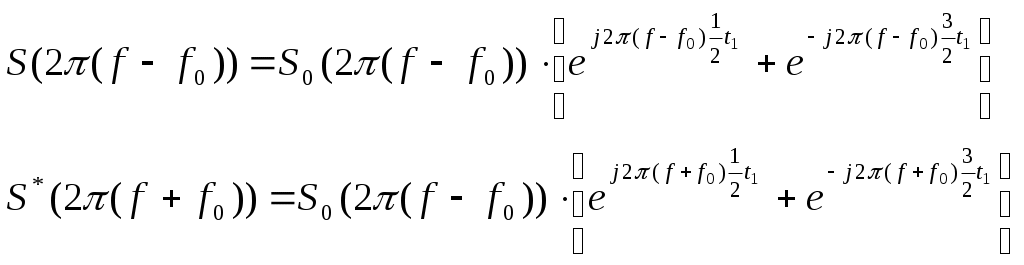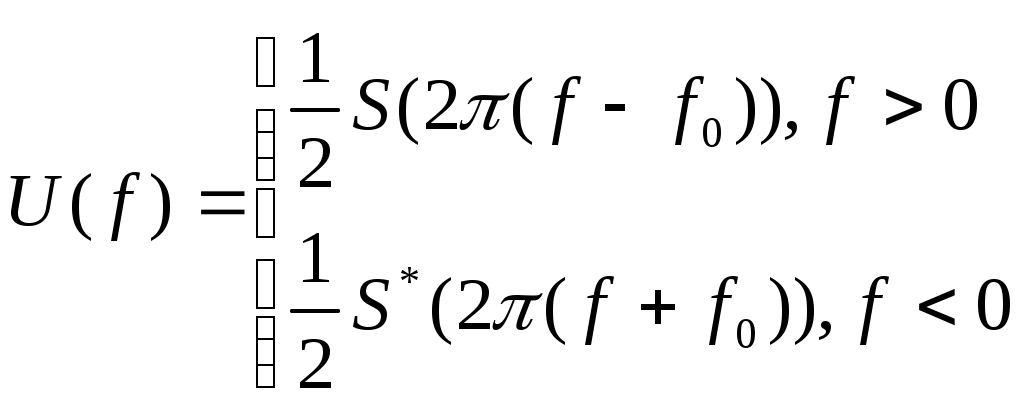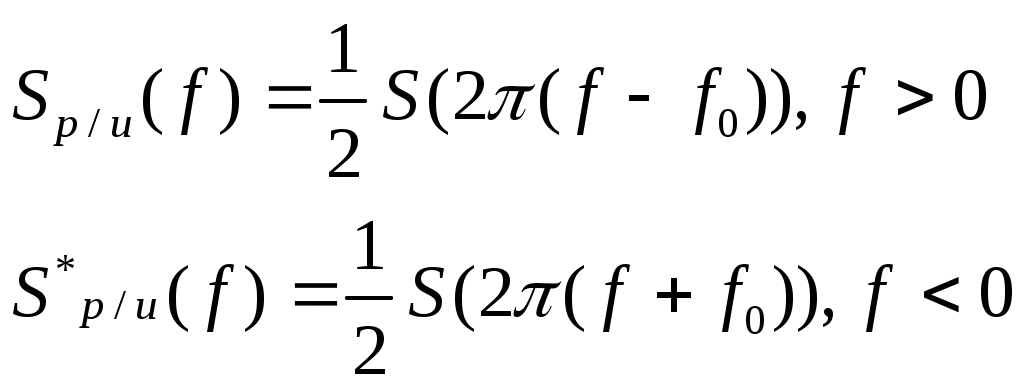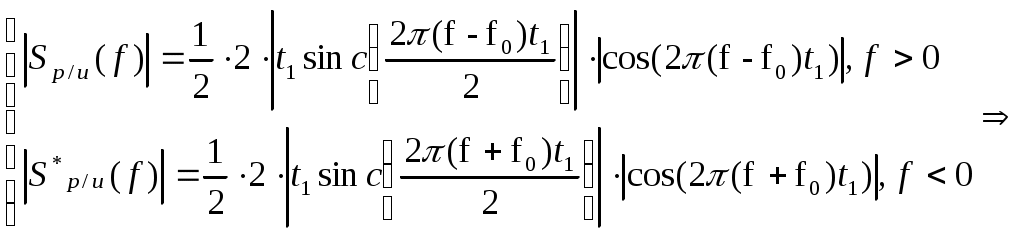







4. Спектральный анализ периодической последовательности радиоимпульсов.
Спектральный анализ сигнала в виде периодической последовательности радиоимпульсов основан на его представлении в виде ряда Фурье:

,

коэффициенты которого связаны с коэффициентами ряда Фурье периодического видеосигнала (3) соотношением:



V_n– амплитудный спектр периодической последовательности радиоимпульсов.
Аналитическое выражение для последовательности радиоимпульсов: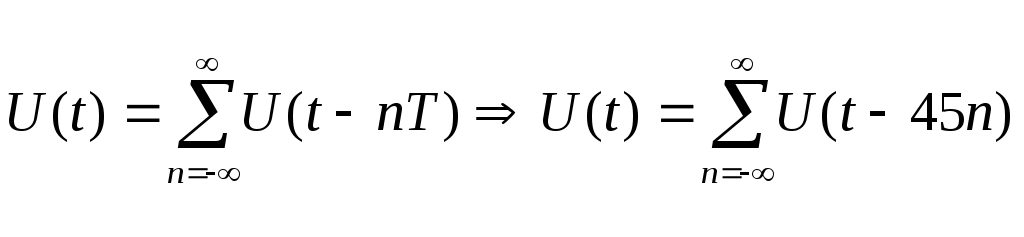



U(t) – одиночный радиоимпульс

или



Временная диаграмма периодической последовательности радиоимпульсов представлена на рис.10.
,



Определим амплитудный спектр периодической последовательности радиоимпульсов по: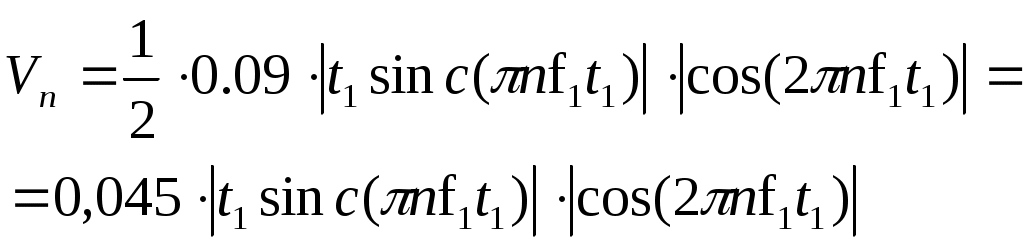

График амплитудного спектра периодической последовательности радиоимпульсов V_n представлен на рис.11
5. Корреляционный анализ непериодического сигнала

Автокорреляционная функция определяется следующим интегралом:
, (7)
и характеризует взаимосвязь между значениями сигнала в различные моменты времени.

Для действительного сигнала корреляционная функция является действительной чётной функцией

Максимального значения, равного энергии сигнала корреляционная функция достигает при τ=0:



Непосредственное интегрирование в формуле (7) даёт выражение для правой ветви автокорреляционной функции (рис.)

Замена в полученном выражении τ =| τ | позволяет перейти к аналитическому описанию автокорреляционной функции, как для положительных значений τ>0, так и для отрицательных τ<0.
По свойствам автокорреляционной функции
S(t±t₀), t₀>0 => R(τ)=R(τ)
Корреляционная функция пачки импульсов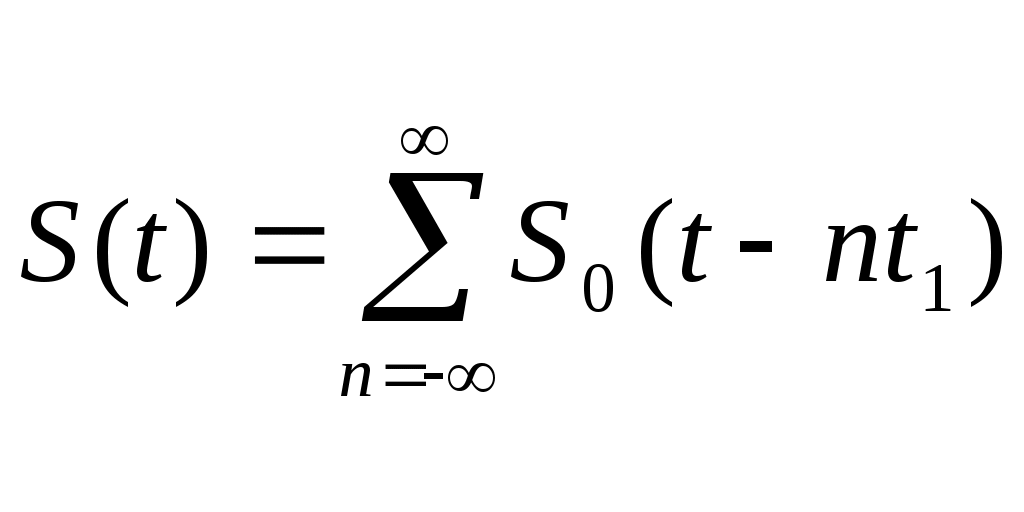

, где S(t) – 1-й импульс в пачке,

при условии, что интервал следования в пачке t₁ больше или равен τ₀ – длительность 1-го импульса в пачке S₀(t), взаимосвязана с корреляционной функцией R₀(τ) соотношением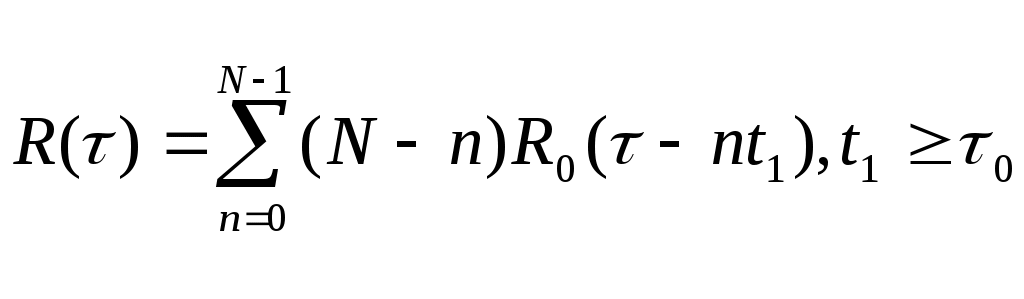

, (8)

6.Спектральный анализ линейной цепи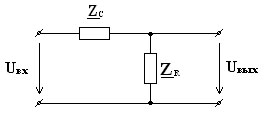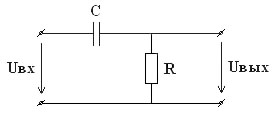


рис.13. Заданная схема цепи рис.14. Эквивалентная схема замещения
КЧХ определяется по следующей формуле:



Согласно эквивалентной схеме замещения:
;
По формуле делителя напряжения [5]: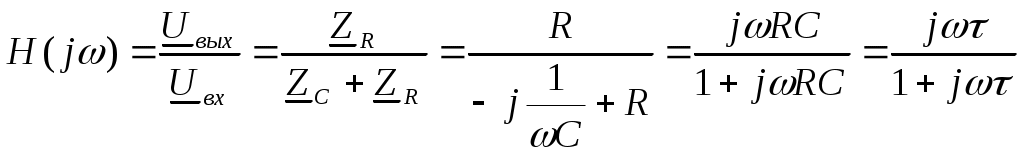




– постоянная RC цепи [5].

Определим АЧХ:



Определим ФЧХ:




Определим значения H(ω) и Ψ(ω) на частотах ω=0 и ω= ,



Графики АЧХ и ФЧХ приведены на рис.15
Аналитическое выражение для спектральной плотности сигнала на выходе цепи (рис.13), при воздействии в виде заданного сигнала S(t) (рис.1):



Амплитудный спектр сигнала на выходе цепи (рис.13), при воздействии в виде заданного сигнала S(t):



График амплитудного спектра сигнала на выходе цепи (рис.13) при воздействии в виде заданного сигнала S(t) представлен на рис.16


Список литературы.
1. Денисенко А.Н., Стеценко О.А. Теоретическая радиотехника: Справочное пособие ч.1: Детерминированные сигналы (методы анализа). – М.: Издательство стандартов, 1993. - 215с.

2. Денисенко А.Н., Стеценко О.А. Спектральный анализ сигналов: Учеб. пособие / Моск. ин-т радиотехники, электроники и автоматики.­– М., 1991. – 76 с.

3. Денисенко А.Н., Стеценко О.А. Линейные радиотехнические цепи: Учеб. пособие / Моск. ин-т радиотехники, электроники и автоматики. – М., 1992. – 78 с.

4. Нефёдов В.И. Основы радиоэлектроники и связи: Учебник для вузов –

2-е изд., перераб. и доп. – М.: Высш.шк., 2002. – 510 с.: ил.

5. Попов В.П. Основы теории цепей: Учеб. для вузов. – 3-е изд., испр.– М.: Высш. шк., 2000 – 575с.: ил.

6. Конспект лекций и семинарских занятий по курсу РТЦ и С.

7. Конспект лекций и семинарских занятий по курсу ОТЦ (2 курс).