Курсовая 3318113. 1 Спектральный анализ дискретизируемого сигнала
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
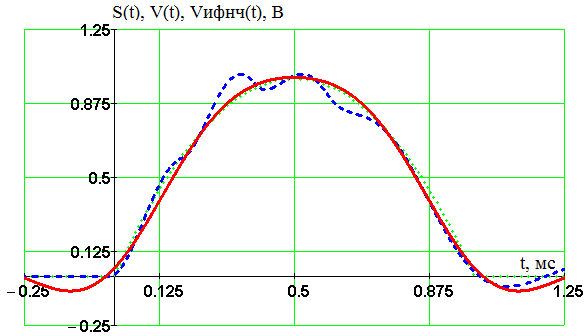 Рисунок 20 - временные диаграммы исходного непрерывного (пунктирная линия) и восстановленных реальным (штриховая линия) и идеальным (сплошная линия) фильтрами нижних частот сигналов Рисунок 20 наглядно иллюстрирует улучшение формы восстановленного сигнала при теоретическом восстановлении с помощью идеального фильтра нижних частот. Это происходит потому, что АЧХ идеального фильтра равномерная на всех частотах полосы пропускания, то есть все спектральные составляющие усиливаются в одинаковое число раз, а спектральные составляющие ненужных копий не попадают на выход за счет равенства нулю АЧХ вне полосы пропускания. К тому же при восстановлении идеальным фильтром нет погрешности, связанной с неодинаковым запаздыванием во времени разных частотных составляющих спектра сигнала, так как для идеального фильтра нижних частот время запаздывания не зависит от частоты. 7 Исследование качества восстановления сигнала при разных значениях длительности исходного сигнала В данном разделе предполагается, используя реальный фильтр нижних частот, проследить зависимость погрешности восстановления от длительности исходного непрерывного сигнала. Пусть частота среза фильтра постоянна и равна Fc=2 кГц. Построим график зависимости погрешности восстановления от длительности исходного сигнала и от частоты дискретизации. Рассчитаем к нему таблицу значений. Методика расчета изложена в пункте 5. При этом следует иметь в виду, что частота среза фильтра теперь является константой. Тогда погрешность восстановления рассчитывается по формуле (29). 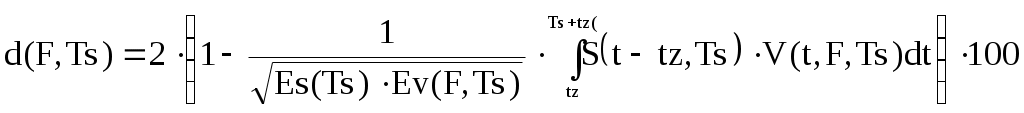 (29) (29)На рисунке 21 изображена полученная зависимость, результаты расчета занесены в таблицу 3. 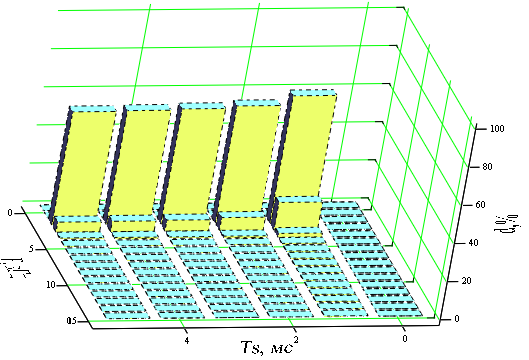 Рисунок 21 – Зависимость погрешности восстановления от частоты дискретизации и от длительности исходного сигнала при оптимальной частоте среза Таблица 3 – Зависимость погрешности восстановления от частоты дискретизации и от длительности исходного непрерывного сигнала при частоте среза Fc=2 кГц.
Таким образом, находим, что для восстановления сигнала с погрешность d= 1% можно использовать частоту дискретизации четыре килогерца, для этого достаточно увеличить длительность исходного сигнала до двух миллисекунд, причем частоту среза надо взять, равной двум килогерцам. Временная диаграмма восстановленного сигнала, соответствующая данным преобразованиям, изображена на рисунке 22. 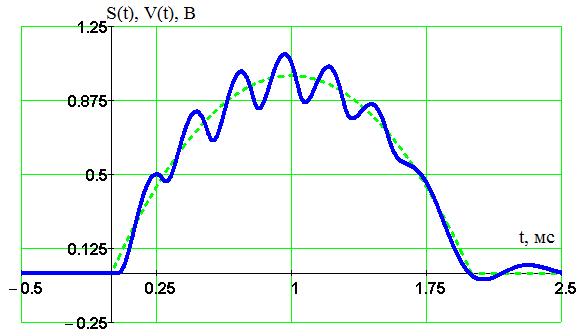 Рисунок 22 - Временные диаграммы исходного непрерывного сигнала, длительностью две миллисекунды (пунктирная линия) и восстановленного с погрешностью d=1% сигнала (сплошная линия) при частоте дискретизации четыре килогерца и частоте среза фильтра два килогерца Теперь частоту дискретизации возьмем постоянной и равной F=5 кГц, и будем исследовать зависимость погрешности восстановления сигнала от длительности импульса и от частоты среза АЧХ реального фильтра. Соответствующие результаты отображены на рисунке 23 и в таблице 4. Расчет произведен по формуле 30. 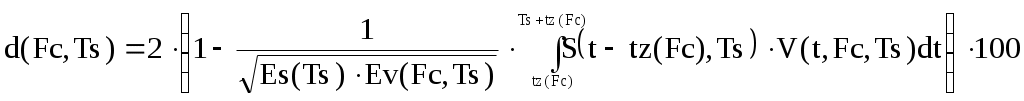 (30) (30)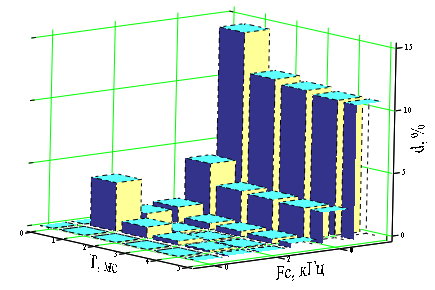 Рисунок 23 – зависимость погрешности восстановления от частоты среза АЧХ фильтра и от длительности исходного сигнала при оптимальной частоте дискретизации Таблица 4 – Зависимость погрешности восстановления от частоты среза АЧХ фильтра и от длительности исходного непрерывного сигнала при оптимальной частоте дискретизации
Таким образом, получаем, что для восстановления сигнала с погрешность d=1% можно нельзя использовать фильтр с частотами среза большими двух килогерц, если не менять частоту дискретизации. Таким образом, в ходе проведенного на данном этапе исследования, приходим к выводу, что погрешность восстановления, требуемую техническим заданием, можно обеспечить, меняя длительность исходного непрерывного сигнала. При этом можно варьировать одновременно частотами среза фильтра и дискретизации, выбирая подходящий в зависимости от условий практической реализации вариант. 8 Проверка основных результатов работы с помощью схемотехнического моделирования Структурная схема установки представлена на рисунке 24. 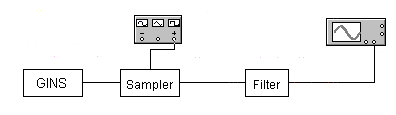 Рисунок 10 - Структурная схема установки 8.1 Моделирование сигнала подлежащего дискретизации (блок GINS) Генератор сигнала показан на рисунке 25. Для его создания были применены метод интегрирования и коммутаций сигнала включения в моменты времени, лежащие в диапазоне от 0 до 0.0005 мс. 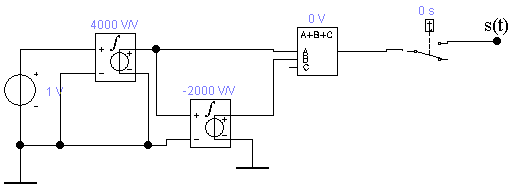 Рисунок 25 - Схема генератора сигнала (блок GINS) На рисунке 26 изображен сигнал, моделируемый схемой. 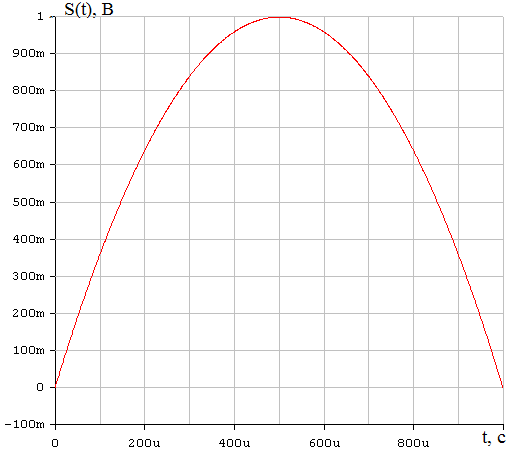 Рисунок 26 – исходный непрерывный сигнал Сопоставляя рисунок 26 с рисунком 1, приходим к выводу, что эти сигналы совпадают. С помощью команды "Fourier Analysis…" построим спектральную плотность амплитуд исходного сигнала (рисунок 27). 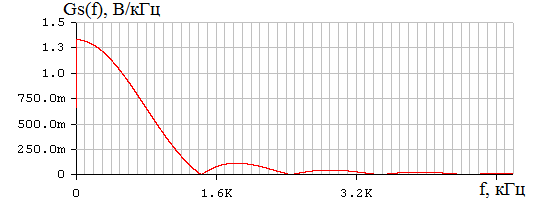 Рисунок 27 - спектральная плотность амплитуд исходного непрерывного сигнала Поскольку анализ спектральных характеристик в программе Electronic Workbench ориентирован преимущественно на исследование периодических сигналов, то при сопоставлении спектральных плотностей, моделированной и рассчитанной теоретически (рисунок 2), будем получать отличие их масштабов в два раза. В симуляторе спектральная плотность амплитуд строится на основе амплитудного спектра, который всегда вдвое больше комплексного. Следует заметить, что данное отличие не играет важной роли, так как изменение масштаба не есть искажение. Таким образом, первый этап моделирования завершен – схема, реализующая заданный сигнал собрана. 8.2 Моделирование процедуры дискретизации Дискретизированный сигнал можно реализовать путем стробирования исходного непрерывного сигнала периодической последовательность малых по длительности импульсов, повторяющихся с частотой дискретизации. Тогда получим схему, представленную на рисунке 28. 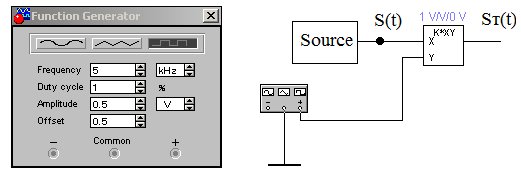 Рисунок 28 – Схема дискретизатора На рисунках 29 и 30 изображены соответственно временные диаграммы исходного и дискретизированного сигналов и спектральная плотность амплитуд дискретизированного сигнала. Частота дискретизации равна 5 кГц. 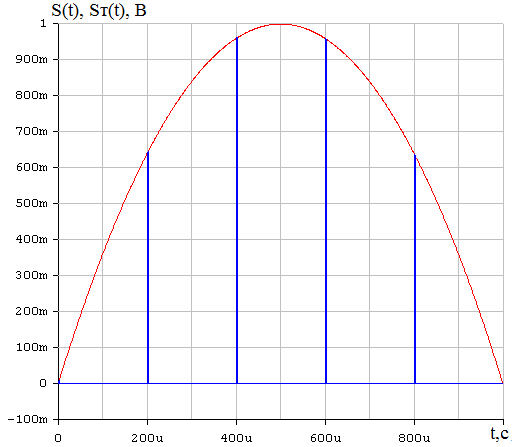 Рисунок 29 - Временные диаграммы исходного и дискретизированного сигналов 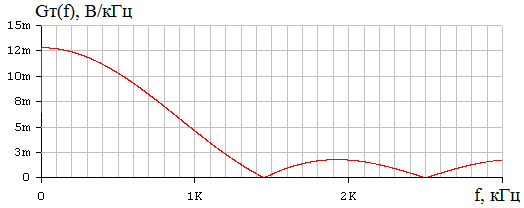 Рисунок 30 - Спектральная плотность амплитуд дискретизированного сигнала Таким образом, анализируя рисунки 29 и 30, приходим к выводу, что моделирование совпадает с расчетом. Второй этап моделирования завершен. 8.3 Имитация процесса восстановления непрерывного сигнала по его дискретным отсчетам Процесс восстановления сигнала обеспечивается путем его фильтрации фильтром нижних частот. Смоделируем ФНЧ по заданной передаточной функции фильтра, определяемой выражением 31. Для этого можно использовать два звена Transfer Function Block. Значения коэффициентов первого и второго звеньев приведены ниже. А10= B10= B11= B12=0 B12= 0 А20= B20= B21= B22=1 B22= 1 На рисунке 31 приведена структурная схема фильтра, на рисунке 32 – его АЧХ. 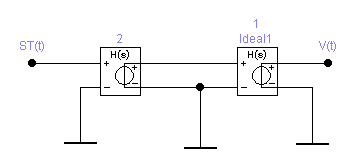 Рисунок 31 – Cхема восстанавливающего фильтра 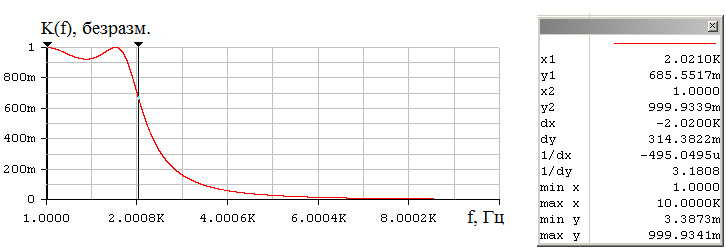 Рисунок 32 – АЧХ восстанавливающего фильтра Рисунок 32 – АЧХ восстанавливающего фильтраПолученная АЧХ совпадает с рассчитанной теоретически. Это подтверждает правильность исследований. Таким образ, полная виртуальная лабораторная установка смоделирована и изображена на рисунке 33. 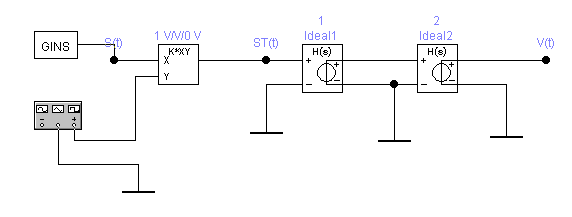 Рисунок 33 – Виртуальная лабораторная установка С помощью собранной установки проверим теоретические расчеты восстановленного сигнала, пронаблюдав сигнал на выходе фильтра. Временные диаграммы восстановленного и исходного сигналов изображена на рисунке 34. 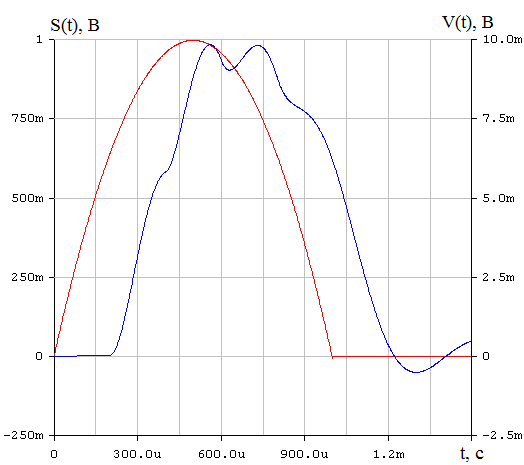 Рисунок 34 - Временные диаграммы восстановленного и исходного сигналов Если сравнивать рисунки 34 и 17, то различия в формах восстановленных сигналов не наблюдаются. Таким образом, моделирование подтверждает правильность расчетов. Данная установка позволяет также исследовать погрешность восстановления при изменении частоты дискретизации. Для этого сначала увеличим в два раза, а затем уменьшив в такое же количество раз, частоту дискретизации и пронаблюдаем осциллограммы входного и выходного сигналов. Результаты изображены на рисунках 35 и 36. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
