экзамен. 1. Строим уравнение регрессии, используя Анализ данных Регрессия
 Скачать 0.97 Mb.
|
 1. Строим уравнение регрессии, используя Анализ данных - Регрессия Получили уравнение: Y=-190,708+138,164X Коэффициент регрессии b=138,164 показывает, что при увеличении дохода на 1 тыс.у.е. величина сбережений увеличивается в среднем на 138,164 у.е. 2. 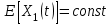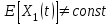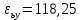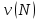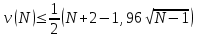Проведем проверку предпосылок МНК Проверим гипотезу Н0 и ее альтернативу Н1: H0:  H0:  Проверка гипотезы с помощью критерия серий: Находим значение медианы:  Составляем последовательность знаков Найдем статистики  и  и проверим неравенства: 1)  2) 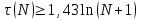 .Имеем число серий: v(n) = 8, длина самой длинной серии K(n) =3. Правые части неравенств равны: 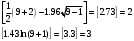 Так как 6>2, первое неравенство не выполнено. Из этого делаем вывод: в рассматриваемом ряде динамики присутствует случайная составляющая 2. Математическое ожидание возмущения равно нулю Данная предпосылка всегда выполняется для линейных моделей 3. Дисперсия возмущения одинакова для всех наблюдений результата Y Это условие называется условием гомоскедастичности или равноизменчивости возмущений. Проверка данной предпосылки методом Голдфельда–Квандта. Сортируем данные по возрастанию Х и разбиваем на две совокупности по 4 наблюдения Находим уравнение регрессии для каждой совокупности используя функцию ЛИНЕЙН() и выписываем суммы квадратов остатков
Так как SS1>SS2 , то F-статистику рассчитываем по формуле: Fрасч=SS1/SS2=6,88 Fтабл=19,00 Т.к. 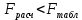 , следовательно возмущение модели гомоскедастично4. Проверяем наличие автокорреляции в остатках. Наличие (отсутствие) автокорреляции в отклонениях проверяют с помощью критерия Дарбина-Уотсона. Численное значение коэффициента равно  где 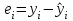 . Т.к. du=0.998 5. Проверим нормальность остатков Строим гистрограмму с помощью Анализ-данных – Гистограмма  Не подтверждается нормальность ряда остатков получим точечный прогноз подставив в модель значение Х= 2,2 (т.к. исходные данные в тысячах у.е.), затем построим интервальную оценку, применяя формулы 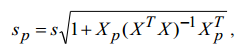  Значение стандартной ошибки получено из итогов регрессии  Отразим графически результаты моделирования  Отметим, что сбережения не могут быть отрицательными, поэтому можем говорить о низкой точности прогноза |