Тестирование предпосылок теоремы Гаусса-Маркова. Пермякова ПЕ_ДЭКФ21-1М. Тестирование предпосылок теоремы ГауссаМаркова
 Скачать 114.44 Kb. Скачать 114.44 Kb.
|
𝑁(0, 𝜎2). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Страна | Индекс человеческого развития, y | Суточная калорийность питания, тыс. ккал на душу населения, x |
| Индия | 0,545 | 2,415 |
| Россия | 0,747 | 2,704 |
| Украина | 0,721 | 2,753 |
| Китай | 0,701 | 2,844 |
| Финляндия | 0,913 | 2,916 |
Продолжение таблицы 1
| Австралия | 0,922 | 3,001 |
| Канада | 0,932 | 3,056 |
| Белоруссия | 0,763 | 3,101 |
| Швеция | 0,923 | 3,16 |
| Чехия | 0,833 | 3,177 |
| Великобритания | 0,918 | 3,237 |
| Нидерланды | 0,921 | 3,259 |
| Швейцария | 0,914 | 3,28 |
| Испания | 0,894 | 3,295 |
| Германия | 0,906 | 3,33 |
| Австрия | 0,904 | 3,343 |
| Польша | 0,802 | 3,344 |
| Норвегия | 0,927 | 3,35 |
| Италия | 0,9 | 3,504 |
| Бельгия | 0,923 | 3,543 |
| Франция | 0,918 | 3,551 |
| США | 0,927 | 3,642 |
| Дания | 0,905 | 3,808 |
Процедуры проведения расчетов:
1. При помощи функции «ЛИНЕЙН» получим таблицу оценок:
Таблица 2
Оценки, полученные с помощью функции «ЛИНЕЙН»
| 0,227 | 0,134 |
| 0,045 | 0,146 |
| 0,544 | 0,069 |
| 25,022 | 21,000 |
| 0,120 | 0,101 |
Оцененная модель: 𝑦𝑡 =0,134+0,227∙𝑥𝑡 + 𝜀̃𝑡, 𝑡=1, ..., 23.
(0,146) (0,045) (0,069)
2. Значения 𝐹 = 25,02 и 𝑅2 = 0,54 также выписываются из результатов, получаемых с помощью «ЛИНЕЙН».
𝐹кр(𝛼 = 0,05, 𝑑𝑓1 = 1, 𝑑𝑓2 = 21) = 4,325 получаем с помощью функции «𝐹. ОБР. ПХ».
Далее выполняется проверка неравенства: 𝐹>𝐹крит: 25,02> 4,32, следовательно, нет оснований принять нулевую гипотезу о незначимости коэффициента детерминации, т.е. коэффициент детерминации признается статистически значимым.
Смысл полученного значения коэффициента детерминации: 𝑅2 = 0,54 – доля дисперсии эндогенной переменной, объясненная уравнением регрессии.
Проверка статистической значимости оценок коэффициентов модели:
𝐻0: 𝑎0=0
𝐻1: 𝑎00
|𝑡0| = a0/Sao = 0,134/0,146 ≈ 0,919
Значение 𝑡крит. получаем с помощью функции «СТЬЮДЕНТ.ОБР.2Х». 𝑡крит(𝛼 = 0,05, 𝑑𝑓2 = 21) = 2,08
0,919<2,08, следовательно, нет оснований отвергнуть гипотезу о незначимости свободного члена, коэффициент 𝑎0 признается незначимым.
𝐻0: 𝑎1=0
𝐻1: 𝑎10
|𝑡1| = a1/Sa1 =0,227/0,045≈ 5,002
5,002>2,08, следовательно, нет оснований принять гипотезу о незначимости коэффициента 𝑎1, коэффициент 𝑎1 признается значимым.
3. Для проведения теста Голдфелда-Квандта необходимо упорядочить выборку по возрастанию значений регрессора – суточной калорийности питания. Воспользуемся инструментом «Сортировка и фильтр» вкладки «Главная» (предварительно выделив всю выборку, включая данные по эндогенной переменной и заголовки): выберем пункт выпадающего меню «Сортировка и фильтр», в открывшемся окне установим «Сортировать по» – «Суточная калорийность питания...» (рис.1).
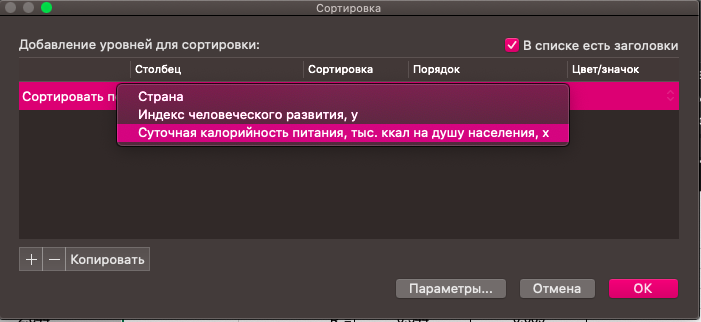
Рисунок 1. Инструмент «Сортировка и фильтр»
Далее разделим выборку на 3 части: 𝑛’=n/3=23/3≈ 8, - и оценим две модели с исходной спецификацией, т.е. 𝑦𝑡 = 𝑎0 + 𝑎1 ∙ 𝑥𝑡 + 𝜀𝑡, где 𝑦 – индекс человеческого развития (отсортированные данные), 𝑥 – суточная калорийность питания населения (отсортированные данные), 𝑡 = 1, ... ,8 – для первой трети выборки, 𝑡 = 16, ... ,23 – для последней трети.
Таблица 3
Оценки, полученные с помощью функции «ЛИНЕЙН», по двум отсортированным частям выборки
| Первая выборка | | Вторая выборка | ||||
| 0,484 | -0,597 | | 0,094 | 0,571 | ||
| 0,146 | 0,416 | | 0,095 | 0,334 | ||
| 0,648 | 0,086 | | 0,140 | 0,041 | ||
| 11,040 | 6,000 | | 0,976 | 6,000 | ||
| 0,082 | 0,045 | | 0,002 | 0,010 | ||
Вычислим наблюдаемые значения статистик:
𝐺𝑄 = 𝑅𝑆𝑆1/RSS2 = 4,36;
𝐺𝑄-1= 𝑅𝑆𝑆2/RSS1=0,229.
Гипотеза о гомоскедастичности принимается в том случае, если одновременно выполняются оба неравенства:
𝐺𝑄<𝐹крит(𝛼, 𝑑𝑓1=n’-(𝑘+1), 𝑑𝑓2=n’-(𝑘+1)),
𝐺𝑄-1<𝐹крит(𝛼, 𝑑𝑓1=n’-(𝑘+1), 𝑑𝑓2=n’-(𝑘+1)).
𝐹крит(0,05, 6, 6) = 𝐹.ОБР.ПХ(0,05; 6; 6) = 4,284.
Таким образом, в данной задаче: 4,36> 4,284, значит, одно из неравенств не выполняется, и нет оснований принять гипотезу о постоянстве дисперсии случайных возмущений, остатки признаются гетероскедастичными.
Список использованных источников
1. Галочкин, В.Т. Учебное пособие по эконометрике для бакалавров // М.: Финансовый университет, департамент анализа данных, принятия решений и финансовых технологий, 2019. – 199 с.;
2. Костромин, А.В. Эконометрика: учебное пособие / А.В. Костромин, Р.М. Кундакчян. – Москва: КНОРУС, 2021. – 228 с.;
3.Бакушева, Г.В. Задачи для подготовки к практической части экзамена по дисциплине «Эконометрика» // М.: Финансовый университет при Правительстве Российской Федерации, 2019. – 38 с..

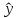 = 𝑏0 + 𝑏1𝑥,
= 𝑏0 + 𝑏1𝑥,