Задачи ТД. 1 техническая термодинамика

• Название: 1 техническая термодинамика
• Дата: 22.01.2022
• Размер: 266.5 Kb.
• Имя файла: Задачи ТД.doc
• Тип: Решение; #338669

1 ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА

1. Параметры состояния тела

Примеры решения задач

1. Давление воздуха по ртутному барометру равно 770 мм при 0° С. Выразить это давление в барах и Па.

Решение

1мм рт. ст. = 133,3 Па, 770 мм рт. ст. =102700 Па = 1,027 бар.
2. Определить абсолютное давление пара в котле, если манометр показывает Р = 1,3 бар, а атмосферное давление по ртутному барометру составляет 680 мм при t = 25° С.

Решение

Показание барометра получено при температуре t = 25° С. Это показание необходимо привести к 0 ºС по уравнению (5):

Р_о = Р_t (1 - 0,000172 t) = 680 · 0,9957 = 677,1 мм рт. ст.

Абсолютное давление пара в котле по формуле (3) равно

Р_абс = 130000 + 677,1 * 133,3 = 0,22 МПа.
3. Давление в паровом котле Р = 0,4 бар при барометрическом давлении 725 мм рт. ст. Чему будет равно избыточное давление в котле, если показание барометра повысится до 785 мм рт. ст., а состояние пара в котле останется прежним? Барометрическое давление приведено к 0 °С.

Решение

Абсолютное давление в котле

Р_абс = 400000 + 725 * 133,3 = 136642 Па

Избыточное давление при показании барометра 785 мм рт. ст.

Р_изб = 136642 – 785 * 133,3 = 32000 Па.
4. Ртутный вакуумметр, присоединенный к сосуду, показывает разрежение 420 мм при температуре ртути в вакуумметре t = 20 °С. Давление атмосферы по ртутному барометру 768 мм при температуре t = 18 °С. Определить абсолютное давление в сосуде.

Решение

Приводим показания вакуумметра и барометра к температуре ртути 0 °С (уравнение 5):

Р_вак = 420 (1—0,000172 * 20) = 418,5 мм рт. ст.

Р_атм = 768 (1—0,000172 * 18) = 765,6 мм рт. ст.

Абсолютное давление в сосуде по формуле (4)

Рабс = 765,6 – 418,5 = 347,1 мм рт. ст. = 46,3 кПа.
5. Водяной пар перегрет на 45 °С. Чему соответствует этот перегрев по термометру Фаренгейта?

Решение

При переводе разности температур, выраженной градусами шкалы Цельсия, в градусы Фаренгейта и наоборот надо исходить только из цены деления того и другого термометров. Поэтому формула (8) принимает следующий вид:



Следовательно, для нашего случая

Основные газовые законы

Примеры решения задач

6. Какой объем занимает 1 кг азота при температуре 70 °С и давлении 0,2 МПа.

Решение

Из характеристического уравнения для 1 кг газа (16) имеем


7. Во сколько раз объем определенной массы газа при -20 °С меньше, чем при +20°C, если давление в обоих случаях одинаковое?

Решение

При постоянном давлении объем газа изменяется по уравнению (10):

следовательно
8. Определить массу 5 м³ водорода, 5 м³ кислорода и 5 м³ углекислоты при давлении 6 бар и температуре 100 °С.

Решение

Характеристическое уравнение для произвольного количества газа

РV = mRT.

Значение газовой постоянной берем из табл. (приложение А). Получаем

Rн₂. = 4124 дж/(кг·град); Rо₂ = 259,8 дж/(кг·град);

Rco₂ = 188,9 дж/(кг·град).

Следовательно,



Отсюда:




9. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 15 °С. После расходования части кислорода давление понизилось до 7,6 МПа, а температура упала до 10 °С.

Определить массу израсходованного кислорода.

Решение

Из характеристического уравнения (15) имеем

m = P V / R T .

Следовательно, начальная и конечная масса кислорода соответственно равны



Таким образом расход кислорода:


10. Сосуд емкостью 10 м³ заполнен 25 кг углекислого газа. Определить абсолютное давление в сосуде, если температура в нем 27 °С.

Решение

Из характеристического уравнения (15) имеем



11. Определить подъемную силу воздушного шара, наполненного водородом, если объем его равен 1 м³ при давлении 750 мм рт. ст. и температуре 15 °С.

Решение

На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (весов) воздуха и водорода в объеме шара:

,

где g = 9,81 м/сек² — ускорение силы тяжести на уровне земли.

Значения плотностей воздуха и водорода могут быть определены из уравнения состояния (15) :



Значения газовых постоянных могут быть легко вычислены или взяты из табл. (приложение А): R_возд = 287 Дж/(кг·град); Rн₂ = 4124 Дж/(кг·град). Так как давление водорода и воздуха равно 750 мм рт. ст., то



Следовательно, подъемная сила шара


12. Какова будет плотность окиси углерода при 20 °С и 710 мм рт. ст., если при 0 °С и 760 мм рт. ст. она равна 1,251 кг/м³?

Решение

Согласно уравнению (22)

Следовательно,

Примеры решения задач 1 з-н т/д

24.В котельной электрической станции за 20 ч работы сожжены 62 т каменного угля, имеющего теплоту сгорания 28900 кДж/кг. Определить среднюю мощность станции, если в электрическую энергию превращено 18% тепла, полученного при сгорании угля.

Решение

Количество тепла, превращенного в электрическую энергию за 20 ч работы,

Q=62∙1000∙28900∙0,18 = 3,2∙10⁹ кДж.

Эквивалентная ему электрическая энергия или работа

.

Следовательно, средняя электрическая мощность станции

N=89590 / 20 = 4479 кВт.
25. Паросиловая установка мощностью 4200 кВт имеет КПД равный 0,2. Определить часовой расход топлива, если его теплота сгорания равна 25000 кДж/кг.

Решение

По формуле (67) находим выражение для расхода топлива



Часовой расход топлива составит

0,72 ∙ 4200 = 3024 кг/ч.
26. Найти изменение внутренней энергии 1 кг воздуха при изменении его температуры от 300°С до 50°С. Зависимость теплоемкости от температуры принять линейной.

Решение

Изменение внутренней энергии можно определить на основании формулы (53). Рассчитаем среднюю теплоемкость воздуха в данном интервале температур (табл. В.1 приложения):



Следовательно,


Примеры решения задач 2з-н т\д
46. 1 кг кислорода при температуре 127°С расширяется до пятикратного объема; температура его при этом падает до 27ºС. Определить изменение энтропии. Теплоемкость считать постоянной.

Решение

По уравнению (100)


47. 1 кг воздуха сжимается по адиабате так, что объем его уменьшается в 6 раз, а затем при V = const давление повышается в 1,5 раза. Определить общее изменение энтропии воздуха. Теплоемкость считать постоянной.

Решение

Изменение энтропии воздуха в адиабатном процессе будет равно нулю. Изменение энтропии в изохорном процессе определится по формуле (103):



следовательно


48. 10 м³ воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400°С. Сжатие производится: 1) изохорно, 2) изобарно, 3) адиабатно и 4) политропно с показателем политропы n = 2,2. Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, определить энтропию воздуха в конце каждого процесса.

Решение

Находим массу 10 м³ воздуха при нормальных условиях:



Определяем изменение энтропии в каждом из перечисленных процессов:

1) изохорное сжатие



2) изобарное сжатие



3) адиабатное сжатие



4) политропное сжатие


49. В процессе политропного расширения воздуха температура его уменьшилась от 25°С до - 37°С. Начальное давление воздуха 4 бар, количество его 2 кг. Определить изменение энтропии в этом процессе, если известно, что количество подведенного к воздуху тепла составляет 89,2 кДж.

Решение

Количество тепла, сообщаемого газу в политропном процессе на основании уравнения (85) составляет



Подставляя значения известных величин, получаем



Отсюда показатель политропы n = 1,2.

Из соотношения параметров политропного процесса определяем конечное давление: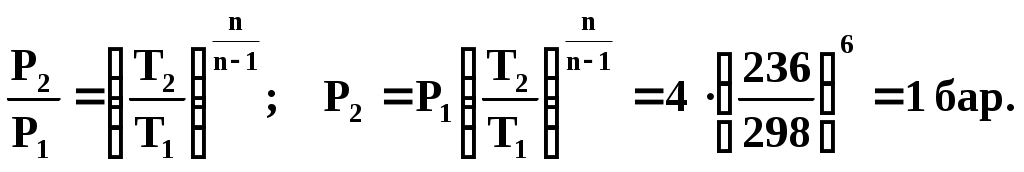



Изменение энтропии по уравнению (101)


50. В сосуде объемом 300 л заключен воздух при давлении 50 бар и температуре 20°С. Параметры среды: Р₀ = 1 бар, t₀ = 20°С. Определить максимальную полезную работу, которую может произвести сжатый воздух, находящийся в сосуде.

Решение

Так как температура воздуха в начальном состоянии равна температуре среды, то максимальная работа, которую может выполнить воздух, может быть получена лишь при условии изотермического расширения воздуха от начального давления Р₁ = 50 бар до давления среды Р₂= 1 бар. Максимальная полезная работа определяется на основании формулы (109):

L_{max (полезн)} = T₀ ∙ (s₂ — s₁) – Р₀ ∙ (V₂ – V₁)

или

L_{max (полезн)} = m∙Т₀ ∙ (s₂ — s₁) — P₀ ∙ (V₂ – V₁).

Определяем массу воздуха, находящегося в сосуде, и объем воздуха после изотермического расширения:



.

Так как изменение энтропии в изотермическом процессе определяется по формуле (106)

то


51. Определить максимальную полезную работу, которая может быть произведена 1 кг кислорода, если его начальное состояние характеризуется параметрами t₁ = 400°С и Р₁ = 1 бар, а состояние среды — параметрами t₀ = 20ºС,Р₀ = 1 бар.

Решение

Максимальная работа, которую произведет при данных условиях кислород, может быть получена лишь при условии перехода его от начального состояния к состоянию среды обратимым путем. Так как температура кислорода в начальном состоянии выше температуры среды, то прежде всего необходимо обратимым процессом снизить температуру кислорода до температуры среды. Таким процессом может явиться только адиабатное расширение кислорода. При этом конечный объем и конечное давление определяются из следующих соотношений: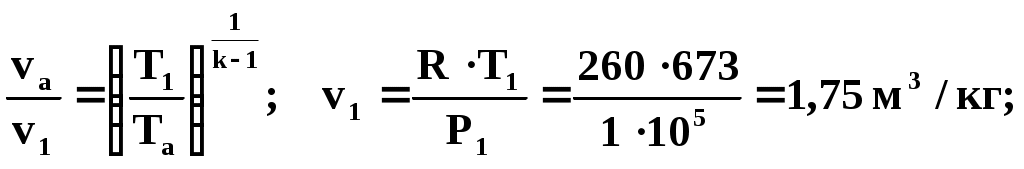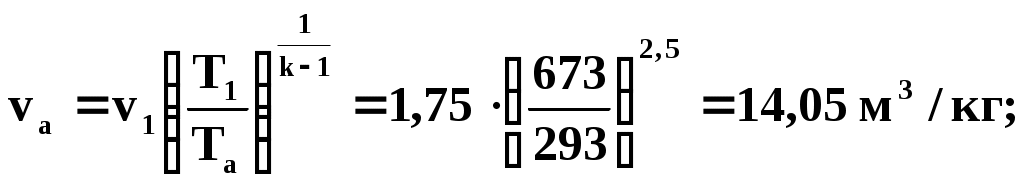

;





После адиабатного расширения необходимо обратимым путем при t = const сжать кислород от давления 0,0542 бар до давления окружающей среды, т. е. осуществить изотермическое сжатие кислорода до 1 бар. При этом конечный объем кислорода



Максимальная полезная работа определяется по формуле (110):



Задача может быть решена также и графическим способом –через площади на PV-диаграмме.
Круговые процессы

Примеры решения задач

52. 1 кг воздуха совершает цикл Карно (см. рис. 2) в пределах температур t₁ = 627°С и t₂ = 27^oС, причем наивысшее давление составляет 60 бар, а наинизшее — 1 бар.

Определить параметры состояния воздуха в характерных точках цикла, работу, термический КПД цикла и количество подведенного и отведенного тепла.

Решение

Точка 1: Р₁ = 60 бар; Т₁ = 900 К. Удельный объем газа определяем из характеристического уравнения (16)



Точка 2: Т₂ = 900 К. Давление находим из уравнения адиабаты (процесс 2-3)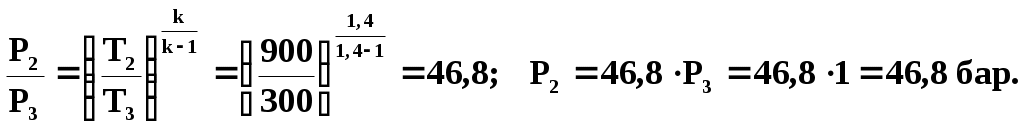



Удельный объем находим из уравнения изотермы (процесс 1-2)



Точка 3: Р₃ = 1 бар; Т₃ = 300 К;



Точка 4: Т₄ = 300 К. Давление воздуха находим из уравнения адиабаты (процесс 4 - 1), удельный объем – из уравнения изотермы (процесс 3 - 4):



Термический КПД цикла



Подведенное количество тепла



Отведенное количество тепла



Работа цикла



Для проверки можно воспользоваться формулой (111):


53. Для идеального цикла поршневого ДВС с подводом тепла при V = const определить параметры в характерных точках, полученную работу, термический КПД, количество подведенного и отведенного тепла, если: Р₁=1 бар; t₁=20^оC, = 3,6; = 3,33; k = 1,4. Рабочее тело - воздух. Теплоемкость принять постоянной.

Решение

Расчет ведемдля I кгвоздуха.

Точка 1: P₁=1бар; t₁=20^oС. Удельный объем определяем из уравнения состояния (15):



Точка 2. Удельный объем находим исходя из степени сжатия



Температура в конце адиабатного сжатия определяется из соотношения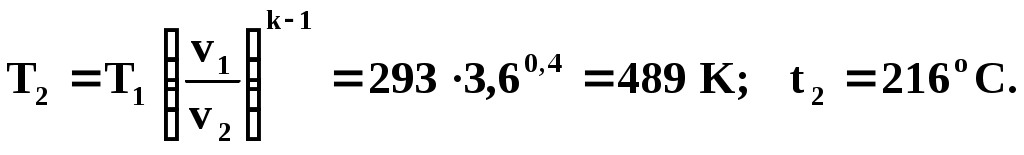



Давление в конце адиабатного сжатия определяем по характеристическому уравнению (15)



Точка 3. Удельный объем v₃=v₂=0,233 м³/кг. Из соотношения параметров в изохорном процессе (линия 2-3) получаем



Следовательно,



Точка 4. Удельный объем v₄=v₁=0,84 м³/кг. Температура в конце адиабатного расширения – уравнение (78)



Давление в конце адиабатного расширения определяем из соотношения параметров в изохорном процессе (линия 4-1):



Определяем количество подведенного и отведенного тепла





Термический КПД цикла определяем по формуле (111)



или по формуле (115)



Работа цикла


54. В идеальном одноступенчатом компрессоре массовой производительностью G=180 кг/чсжимается воздух до давления Р₂=4,9 бар. Определить теоретически необходимую мощность электродвигателя компрессора, отведенное в рубашку цилиндра компрессора тепло и расход охлаждающей воды, если сжатие происходит политропно (п=1,3), а охлаждающая вода нагревается на 25°С. Начальное давление воздуха Р₁=0,98 бари температура t₁=0С.

Решение

Работа, расходуемая на сжатие 1 кг газа в одноступенчатом компрессоре при политермическом режиме, определяется по формуле (125)



Мощность, расходуемая на сжатие газа в компрессоре, определяем по формуле (129)



Удельное количество отведенной теплоты определяем по формуле (85)



Температуру в конце политропного сжатия определяем из соотношения (83)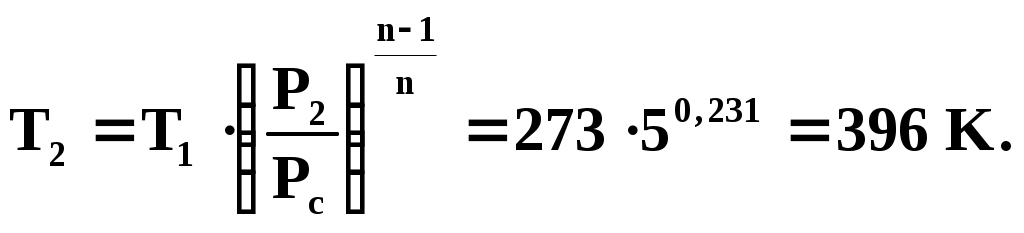



Определяем полное количество отведенной теплоты



Расход охлаждающей воды составляет


55. Определить расход воды на охлаждение воздуха в рубашке двухступенчатого компрессора производительностью 10 м³/мин. в промежуточном и концевом холодильниках, если в холодильниках воздух охлаждается до начальной температуры, а вода нагревается на 15С. Воздух перед компрессором имеет давление Р₁=0,98 бари температуру t₁=10С, сжатие воздуха в компрессоре происходит политропно (п=1,3) до конечного давления Р₂=8,8 бар.

Решение

Количество тепла, отводимого в рубашке компрессора

от 1 кгвоздуха,

;

от G кгвоздуха

.

Количество тепла, отводимого в промежуточном и концевом холодильниках: от 1 кгвоздуха

;

от G кг воздуха

.

Массовую производительности компрессора определяем из характеристического уравнения (15)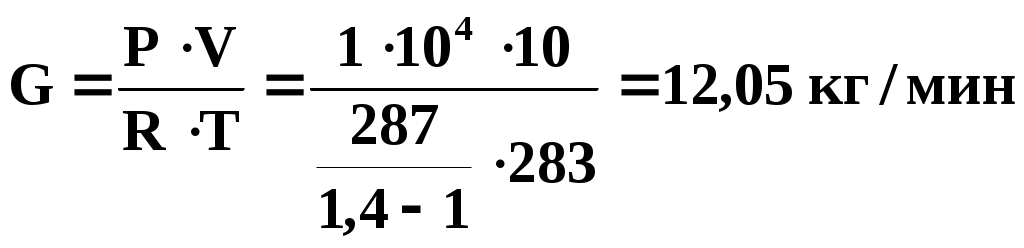

.

Промежуточное давление – уравнения (132) и (133)

.

Температура в конце сжатия – уравнение (83)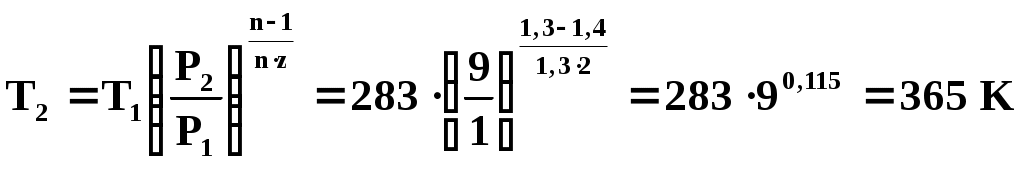

.

Количество тепла, отводимого в рубашке .компрессора,

.

Количество тепла, отводимого в промежуточном и концевом холодильниках,

.

Расход охлаждающей воды

.
Истечение газов и паров. Дросселирование

Опасные и вредные продукты при аллергии

Опасные продукты с высоким уровнем аллергенов:

• 
  морепродукты, большинство сортов рыб, красная и черная икра;
  
• 
  свежее коровье молоко, сыры, цельномолочные продукты; яйца; полукопченые и сырокопченые мясо, колбаса, сардельки, сосиски;
  
• 
  продукты промышленного консервирования, маринованные продукты; соленые, острые и пряные продукты, соусы, приправы и специи; отдельные виды овощей (тыква, красный перец, помидоры, морковь, квашеная капуста, баклажаны, щавель, сельдерей);
  
• 
  большинство фруктов и ягод (клубника, красные яблоки, земляника, малина, ежевика, облепиха, черника, хурма, виноград, вишня, гранаты, дыня, слива, ананасы), соки, кисели, компоты из них;
  
• 
  все виды цитрусовых; сладкая или фруктовая газированная вода, жевательные резинки, ароматизированные ненатуральные йогурты; некоторые виды сухофруктов (курага, финики, инжир);
  
• 
  мед, орехи и все виды грибов; алкогольные напитки, какао, кофе, шоколад, карамель, мармелад; продукты с пищевыми добавками (эмульгаторы, консерванты, ароматизаторы, красители);
  
• 
  экзотические продукты.
  

Полезные продукты при аллергии

Продукты с низким уровнем аллергенов:


кисломолочные продукты (ряженка, кефир, натуральный йогурт, творог); отварное или тушеное нежирное свиное и говяжье мясо, курица, рыба (морс-кой окунь, треска), субпродукты (почки, печень, язык); гречневые, рисовые, кукурузные хлебцы; зелень и овощи (капуста, брокколи, брюква, огурцы, шпинат, укроп, петрушка, зеленый салат, патиссоны, кабачки, репа); овсяная, рисовая, перловая, манная каша; постное (оливковое и подсолнечное) и сливочное масло; некоторые виды фруктов и ягод (зеленые яблоки, крыжовник, груши, белая черешня, белая смородина) и сухофрукты (сушеные груши и яблоки, чернослив), компоты и узвары из них, отвар шиповника, чай и минеральная вода без газа.

•