Случ.велич.№1нов.рус. 1. Тема Случайные величины

• Название: 1. Тема Случайные величины
• Анкор: 13156
• Дата: 05.12.2022
• Размер: 333 Kb.
• Имя файла: Случ.велич.№1нов.рус.doc
• Тип: Документы; #829984

1. Тема: Случайные величины

2. Количество учебных часов – 3 часа (120 мин.)

3. Актуальность темы ( мотивация изучения).

Теория вероятности служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей. Случайные величины являются числом, характеризующим явления случайных событий. Такие характеристики случайных величин, как математическое ожидание, дисперсия, среднее квадратическое отклонение очень важно для решения различных задач математического прогнозирования заболеваний человека.
4. Цели занятия.

Ознакомиться со случайными величинами, их видами и основными характеристиками. Рассмотрение закона распределения случайной величины, функции распределения.

- Студент должен знать:

1. 
   Что такое случайные величины.
   
2. 
   Виды случайных величин.
   
3. 
   Как определяется математическое ожидание дискретной случайной величины.
   
4. 
   Свойства математического ожидания.
   
5. 
   Что такое дисперсия дискретной случайной величины. Что она характеризует.
   
6. 
   Смысл среднего квадратического отклонения случайной величины.
   
7. 
   Как определяется интегральная функция распределения.
   
8. 
   Связь между плотностью распределения вероятности непрерывной случайной величины и функцией распределения.
   
9. 
   Как определяется математическое ожидание для непрерывной случайной величины.
   
10. 
    Среднее квадратическое отклонение непрерывной случайной величины.
    
11. 
    Определение моды, медианы.
    

- Студент должен уметь:

1. 
   Различать виды случайных величин.
   
2. 
   Вычислять математическое ожидание дискретной случайной величины по закону распределения.
   
3. 
   Применять свойства математического ожидания при определении числовой характеристики случайной величины.
   
4. 
   Вычислять дисперсию дискретной случайной величины.
   
5. 
   Определять среднее квадратическое отклонение дискретной случайной величины.
   
6. 
   Строить интегральную функцию распределения.
   
7. 
   Строить дифференциальную функцию распределения.
   
8. 
   Вычислять математическое ожидание непрерывной случайной величины.
   
9. 
   Вычислять дисперсию непрерывной случайной величины.
   
10. 
    Вычислять среднее квадратическое отклонение непрерывной случайной величины.
    

11. Определять моду, медиану.

5. Вопросы для подготовки к занятию.

- по базисным знаниям:

Случайные события. Основные формулы вычисление вероятностей случайных событий. Числовые ряды. Определенный интеграл. Несобственные интегралы.
- по теме занятия:

1. 
   Дайте определение случайной величины.
   
2. 
   Виды случайных величин.
   
3. 
   Дайте определение математического ожидания дискретной случайной величины.
   
4. 
   Назовите свойства математического ожидания.
   
5. 
   Дисперсия дискретной случайной величины.
   
6. 
   Формула для вычисления дисперсии.
   
7. 
   Свойства дисперсии.
   
8. 
   Среднее квадратическое отклонение.
   
9. 
   Функция распределения.
   
10. 
    Свойства функции распределения.
    
11. 
    График функции распределения.
    
12. 
    Плотность распределения.
    
13. 
    Нахождение функции распределения по известной плотности распределения.
    
14. 
    Свойства плотности распределения.
    
15. 
    Математическое ожидание непрерывной случайной величины.
    
16. 
    Дисперсия непрерывной случайной величины.
    
17. 
    Среднее квадратическое отклонение непрерывной случайной величины.
    

6. Информационно- дидактический блок:

Краткая аннотация по теме. Числовые характеристики случайных величин. Функция распределения непрерывной случайной величины и ее график. Дифференциальная и интегральная функция распределения и их графики.
Случайная величина
Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения 0, 1, 2,…, 100.

Будем обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами х, у, z.

Например, если случайная величина Х имеет три возможных значения, то они будут обозначены так: х₁, х₂, х₃.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Например, число посетителей аптеки в течение дня, количество яблок на дереве и др.

Непрерывнойвеличинойназывают случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

К непрерывным случайным величинам можно отнести температуру больного в фиксированное время суток, массу наугат выбранной таблетки некоторого препарата и т.д.
Дискретные случайные величины.
Наиболее полную информацию о дискретной случайной величине дает закон распределения этой величины.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

Х	х1	х2	…	хп
Р			…

Пример 2. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 тыс. тенге и десять выигрышей по 1тыс. тенге. Найти закон распределения случайных величин Х- стоимости возможного выигрыша для владельца одного лотерейного билета.

Решение: Напишем возможные значения х: х₁=50, х₂=1, х₃=0. Вероятности этих возможных значений таковы: Р₁=1/100=0,01, Р₂=10/100=0,1, Р₃=89/100=0,89.

Напишем искомый закон распределения:

Х	50	1	0
Р	0,01	0,1	0,89

Контроль: 0,01+0,1+0,89=1.

Математическое ожидание дискретной

случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина Х может принимать только значения вероятности которых соответственно равны . Тогда математическое ожидание М(х) случайной величины Х определяется равенством



Если дискретная случайная величина Х принимает счетное множество возможных значений, то

(1)

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Пример 4. Найти математическое ожидание случайной величины Х, зная законы ее распределения:

Х	3	5	2
Р	0,1	0,6	0,3

Решение: Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:

М(х)=3 .
Свойства математического ожидания
1⁰. Математическое ожидание постоянной величины равно самой постоянной:

М(С)=С.

2⁰. Постоянный множитель можно выносить за знак математического ожидания:

.

3⁰. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

.

4⁰. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых:

.

Пример 5. Независимые случайные величины заданы следующими законами распределения:

Х	5	2	4
Р	0,6	0,1	0,3

Y	7	9
Р	0,8	0,2

Найти математическое ожидание случайной величины Х, Y.

Решение: Найдем математическое ожидание каждой из данных величин:



Теорема. Математическое ожидание М(х) числа появлений событий А в независимых испытаниях равно произведению этих испытаний на вероятность появления событий в каждом испытании:
.

Отклонение случайной величины от ее

математического ожидания
Пусть Х- случайная величина и М(Х) – ее математическое ожидание. Рассмотрим в качестве новой случайной величины разность Х-М(Х).

Отклонением называют разность между случайной величиной и ее математическим ожиданием.

Отклонение имеет следующий закон распределения:

Х-М(х)	Х1-М(х)	Х2-М(х)	…	Хп-М(х)
Р			…

Теорема. Математическое ожидание отклонения равно нулю:

.
Пример 6. Задан закон распределения дискретной случайной величины Х:

Х	1	2
Р	0,2	0,8

Доказать, что математическое ожидание отклонения равно нулю.
Решение: Найдем математическое ожидание Х: .

Найдем возможные значения отклонения, для чего из возможных значений Х вычтем математическое ожидание .

Напишем закон распределения отклонения:

	-0,8	0,2
Р	0,2	0,8

Найдем математическое ожидание отклонения:



На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.

Дисперсией(рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

(2)

Пример 7. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

Х	1	2	5
Р	0,3	0,5	0,2

Решение: Найдем математическое ожидание:

.

Найдем всевозможные значения квадрата отклонения :







Напишем закон распределения квадрата отклонения:

	1,69	0,09	7,29
Р	0,3	0,5	0,2

По определению, .

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:

(3)

Пример 8. Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

Х	2	3	5
Р	0,1	0,6	0,3

Решение: Найдем математическое ожидание М(х):



Напишем закон распределения случайной величины Х ²:

Х2	4	9	25
Р	0,1	0,6	0,3

Найдем математическое ожидание М(х²):



Искомая дисперсия
Свойства дисперсии
1⁰. Дисперсия постоянной величины С равна нулю: .

2⁰. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

3⁰. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.

Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании .

Среднее квадратическое отклонение
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины Х называют квадратный корень из дисперсии:

(4)

Пример 9. Случайная величина Х задана законом распределения

Х	2	3	10
Р	0,1	0,4	0,5

Найти среднее квадратическое отклонение .

Решение: Найдем математическое ожидание Х:



Найдем математическое ожидание Х ²:

.

Найдем дисперсию:

.

Искомое среднее квадратическое отклонение



Теорема. Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

(4)
Непрерывные случайные величины.
В отличие от дискретной случайной величины непрерывные случайные величины невозможно задать в виде таблицы ее закона распределения поскольку невозможно перечислить и выписать в определенной последовательностей все ее значения. Одним из возможных способов задания непрерывной случайной величины является использование функции распределения.

Функция распределения
Функцией распределения называют функцию , определяющую вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х, т.е. (5)

Иногда вместо термина «Функция распределения» используют термин «Интегральная функция».

Свойства функции распределения
Свойство 1. Значения функции распределения принадлежит отрезку [0;1]:

.

Свойство 2. - неубывающая функция, т.е. если х₂>x₁.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a,b), равна приращению функции распределения на этом интервале

(6).

Пример 10. Случайная величина Х задана функцией распределения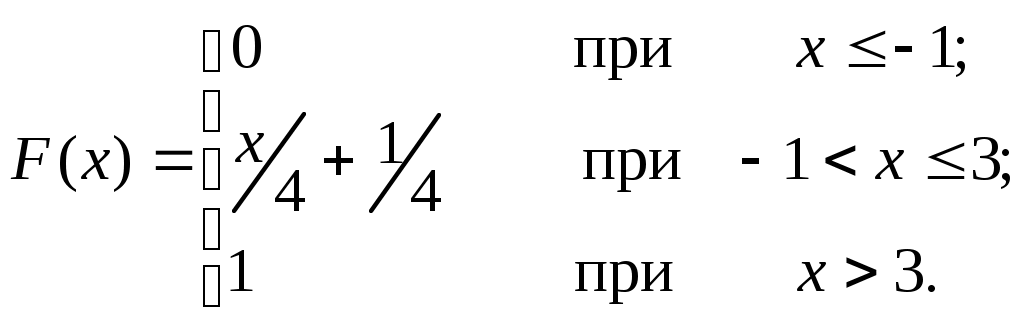



Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0;2):

.

Решение: Так как на интервале (0;2) по условию, ,

то . Итак, .

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Следствие 3. Если возможные значения случайной величины принадлежат интервалу (а;b), то:

1. 
   
   
2. 
   
   

Справедливы следующие предельные соотношения:


График функции распределения
График расположен в полосе, ограниченной прямыми у=0, у=1 (первое свойство). При возрастании х в интервале (а;b), в котором заключены все возможные значения случайной величины, график «подымается вверх».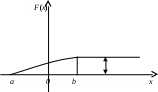




Рисунок 1.
При ординаты графика равны нулю; при ординаты графика равны единице

Пример 11. Дискретная случайная величина Х задана таблицей распределения:

Х	1	4	8
Р	0,3	0,1	0,6

Найти функцию распределения и построить ее график.

Решение: Функция распределения аналитически может быть записана так: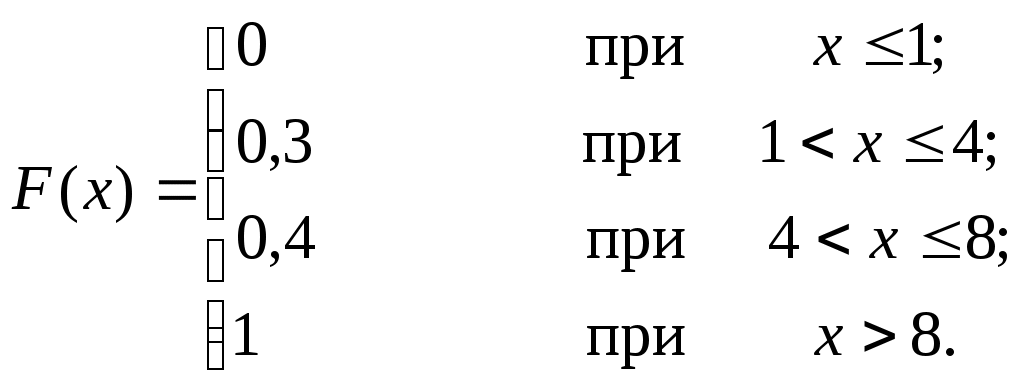



Рисунок 2.


1

Плотность распределения вероятностей непрерывной случайной величины
ОПРЕДЕЛЕНИЕ: Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию - первую производную от функции распределения :

= .

Из этого определения следует, что функция распределения является первообразной для плотности распределения.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а;b) равна определенному интегралу от плотности распределения, взятому в пределах от а доb:

(8)

Свойства плотности распределения вероятностей:

1. 
   Полтность вероятностей является неотрицательной функцией:
   

.

2. 
   Определенный интеграл от до от плотности распределения вероятностей непрерывной случайной величины равен 1.
   

.

3. 
   Определенный интеграл от до от плотности распределения вероятностей непрерывной случайной величины равен функции распределения этой величины:
   

.
Пример 12. Задана плотность распределения вероятностей случайной величины Х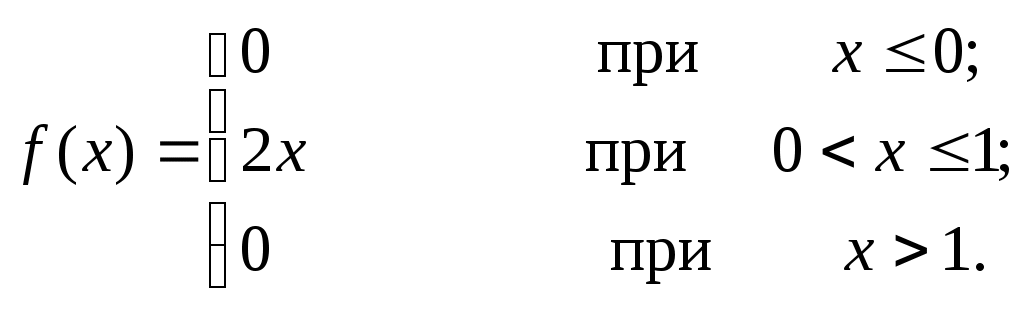



Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5;1).

Решение: Искомая вероятность: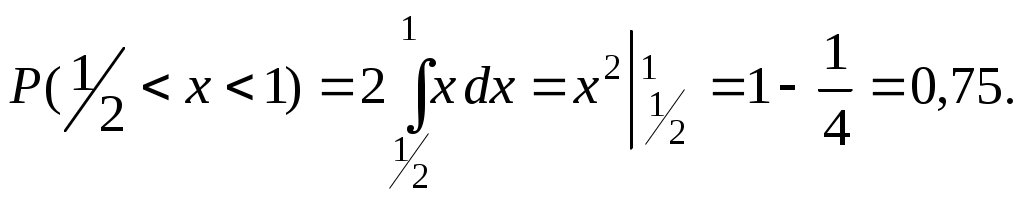



Числовые характеристики непрерывных случайных величин.
Распространим определение числовых характеристик дискретных величин на величины непрерывные.

Пусть непрерывная случайная величина Х задана плотностью распределения .
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a;b], называют определенный интеграл

(8)

Если возможные значения принадлежат всей оси Ох, то

(9)

Модой непрерывной случайной величины X называют то ее возможное значение, которому соответствует локальный максимум плотности распределения.

Медианой непрерывной случайной величины X называют то ее возможное значение, которое определяется равенством:


Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х принадлежат отрезку [a;b], то

(10)

или (10*)

Если возможные значения принадлежат всей оси х, то

(11)

Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

(12)

Пример 13. Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения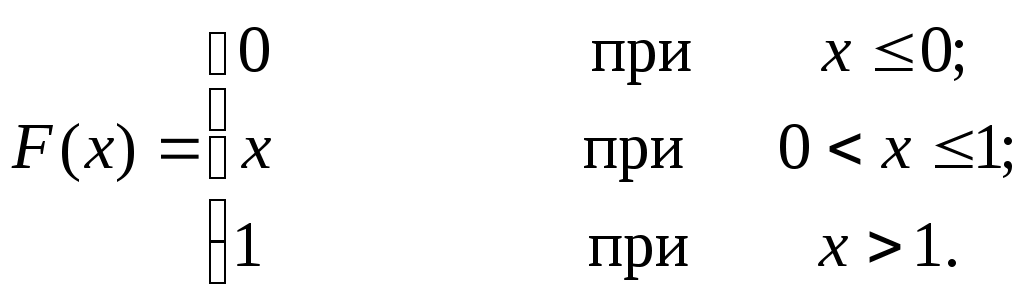



Решение: Найдем плотность распределения: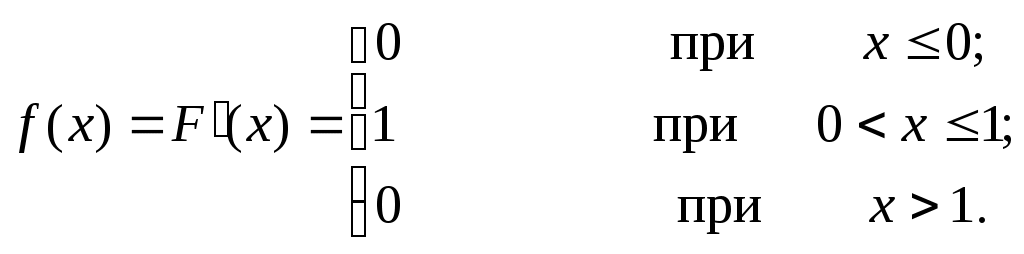



Найдем математическое ожидание по формуле (8):

.

Найдем дисперсию по формуле (10*):



Пример 14. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины, заданной плотностью распределения вероятностей , равной ½ на отрезке [1,3] и 0 во всех остальных точках оси абцисс, т.е на интервалах и .

Решение. Используя формулу (9), для математического ожидания и разбивая первоначальный интеграл на 3 интеграл, последовательно получим:



Используя формулу (10) найдем дисперсию аналогично:

.

И по формуле (12) вычислим среднее квадратическое отклонение

.

7. Содержание знятия.

- Самостоятельная работа.

1. 
   Возможные значения случайной величины: Известны вероятности первых двух возможных значений: Найти вероятность х₃.
   
2. 
   Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:
   

Х	6	3	1
Р	0,2	0,3	0,5

3. Вероятность отказа детали за время испытания на надежность равна 0,2. Найти математическое ожидание числа отказавших деталей, если испытанию будут подвергнуты 10 деталей.

4. Найти дисперсию случайной величины, зная закон ее распределения:

Х	0,1	2	10	20
Р	0,4	0,2	0,15	0,25

5. Случайная величина Х может принимать два возможных значения: х₁ с вероятностью 0,3; и х₂ с вероятностью 0,7; причем х₂> х₁. Найти х₁ и х₂, зная, что и .

6. Случайная величина Х задана функцией распределения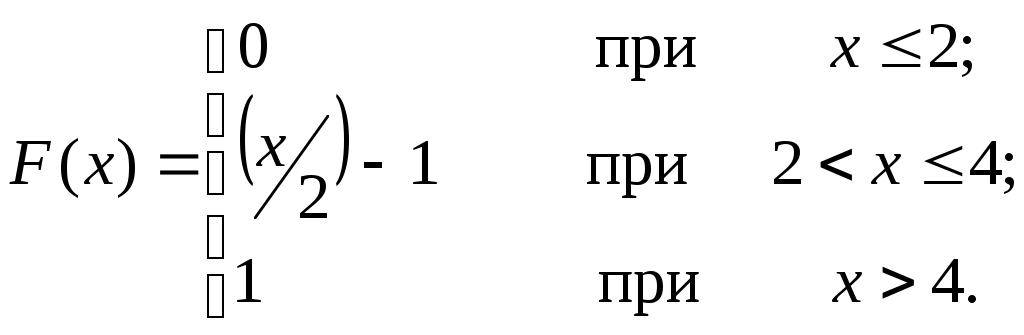



Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (2;3).

7. Случайная величина задана плотностью распределения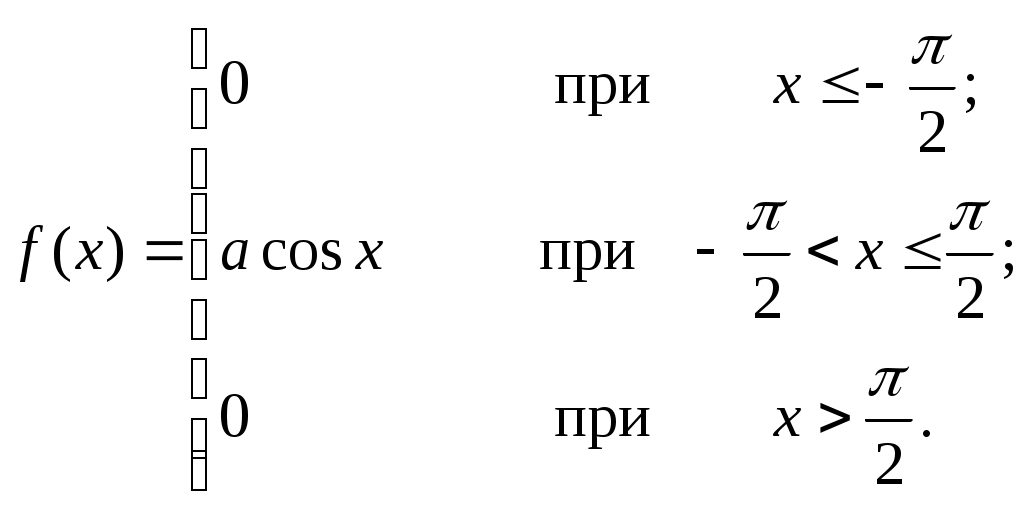



Найти: а) функцию распределения,

б) коэффициент а,

в) вероятность того, что в результате испытания случайная величина примет значение, заключенное в интервале .

8. 
   Найти математическое ожидание и дисперсию случайной величины Х, заданной функцией распределения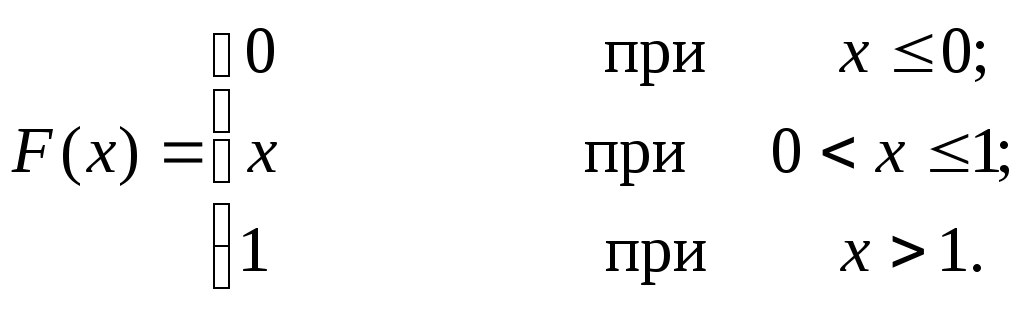
   

Ремизов А.Н. «Сборник задач по медицинской и биологической физике»

Задачи №1.71 - 1.83.

- Работа с преподавателем.

Преподаватель делает разбор общих ошибок студентов при выполнении заданий, останавливается на основных моментах темы.
- Контроль исходного и итогового уровня знаний

Анализ и итог практического занятия по результатам устных, тестовых вопросов по случайным величинам, а также индивидуальных вариантов (карточки) по числовым характеристикам случайных величин.
8. Литература.

1. 
   В. Е. Гмурман. Теория вероятностей и математическая статистика. М., «Высшая школа», 1972 г.
   
2. 
   В. Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистики. М., «Высшая школа», 2001г.
   
3. 
   В.Н.Калинина, В.М. Панкин, Математическая статистика, 2002г.
   
4. 
   Адибаев Б.М. Элементы математической статистики и основы теории верятностей. Учебное пособие, Алматы 2004г.