Курсовая работа на тему Расчет показателей разработки нефтяной залежи при упругом режиме разработки. КУРСОВАЯ. 1. Теоретическая часть Теория упругого режима
 Скачать 5.55 Mb. Скачать 5.55 Mb.
|
|
Содержание Введение 1. Теоретическая часть……………………….…………………………………...3 1.1 Теория упругого режима………………………………………………….......3 1.2 Методика расчета упругого запаса жидкости в пласте……………….……4 1.3 Методика расчета падения пластового давления по времени при режиме постоянного отбора жидкости……………………………………………………7 2. Расчетная часть…………………………………………...…………...………13 2.1 Расчет упругого запаса жидкости в пласте…………………………...……13 2.2 Расчет падения пластового давления по времени при режиме постоянного отбора жидкости…………………………………………………………………16 2.3 Расчет динамики отбора жидкости и пластового давления при режиме постоянной депрессии на пласт………………….……………………………..19 Вывод…...………………………………………………………………………...20 Список использованной литературы………………...…………………………21 Введение В практике разработки и эксплуатации нефтяных и газовых месторождений в пластах часто возникают неустановившиеся процессы, связанные с пуском и остановкой скважин, с изменением темпов отбора флюида из скважин. Характер этих процессов проявляется в перераспределении пластового давления, в изменениях во времени скоростей фильтрационных потоков, дебитов скважин и т.д. Особенности этих неустановившихся процессов зависят от упругих свойств пластов и насыщающих их жидкостей. Это означает, что основной формой пластовой энергии, обеспечивающей приток жидкости к скважинам в этих процессах, является энергия упругой деформации жидкостей (нефти и воды) и материала пласта. Первыми исследователями, разрабатывавшими теорию упругого режима в 30-х годах 20-го века, были Маскет, Шилсуиз, Херст, Тсейс и Джекоб. Однако они не учитывали объемную упругость пласта. Наиболее полно теория упругого режима с учетом упругих свойств твердого скелета пласта и насыщающих жидкостей была разработана В.Н.Щелкачевым. В данной работе поставлены следующие задачи: изучить теорию упругого режима пласта, рассчитать падение пластового давления во времени при режиме постоянного отбора жидкости, рассчитать динамику отбора жидкости и пластового давления при режиме постоянной депрессии на пласт. 1. Теоретическая часть 1.1 Теория упругого режима Одной из основных сил действующий в пластовой системе, является сила горного давления, представляющая вес горных пород (ГП) расположенных над пластом. Под действием этой силы породы пласта- коллектора нефти и газа деформируются и находятся в напряженном состоянии. Согласно молекулярно-кинетической теории строения вещества напряжение состояния ГП характеризуется запас внутренней энергии твердого скелета породы. Показателями этой внутренней энергии могут служить коэффициент упругости.[1] Профессор В. Н. Щелкачев, разработавший суждение об упругом расширении и движении жидкости в упругих пористых средах, ввел понятие «модуль упругости коллектора». Этот коэффициент указывает на отношение объема жидкости к объему породы из-за упругости породы и самой жидкости при падении давления на одну единицу. Когда давление в зоне скважины и пласте уменьшается, порода, нефть и вода расширяются и увеличиваются в объеме, помогая выталкивать нефть на забой скважины. Этот режим известен как упругий.[2] В условиях упругого режима движение жидкости начинается за счет использования потенциальной энергии упругой деформации пласта и жидкости сначала в ближайших окрестностях забоя, затем во все более удаленных областях пласта. В самом деле, при снижении пластового давления упругое противодействие пласта вышележащему горному массиву уменьшается, и это приводит к уменьшению объема порового пространства, что, в свою очередь, увеличивает сжатие жидкости. Все это способствует вытеснению жидкости из пласта в скважину. И несмотря на то, что коэффициенты объемной упругой деформации жидкости и твердого скелета пласта очень малы, из-за того, что очень велики объемы пласта и насыщающих его флюидов, объемы жидкости, извлекаемой из пласта за счет упругости пласта и жидкости, могут быть весьма значительным 1.2 Методика расчета упругого запаса жидкости в пласте Упругий запас жидкости в пласте можно подсчитать следующим образом. Выделим мысленно элемент объема пласта 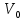 . Пусть . Пусть 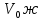 есть объем жидкости, насыщающей этот элемент объема пласта есть объем жидкости, насыщающей этот элемент объема пласта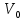 при начальном давлении при начальном давлении 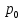 . Упругий запас жидкости будем определять по ее объему, замеряемому при начальном пластовом давлении. Обозначим через . Упругий запас жидкости будем определять по ее объему, замеряемому при начальном пластовом давлении. Обозначим через 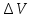 , изменение упругого запаса жидкости внутри объема пласта , изменение упругого запаса жидкости внутри объема пласта 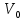 при изменении давления во всех его точках на величину при изменении давления во всех его точках на величину 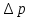 . Тогда, получим: . Тогда, получим: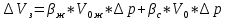 (1) (1)Учтем, что начальный объем жидкости, насыщающей элемент объема пласта 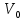 , равен полному объему пор в этом элементе: , равен полному объему пор в этом элементе: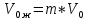 (2) (2)Где m-пористость пласта. Тогда формулу (1) с учетом равенства (2) можно переписать в следующем виде: 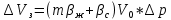 (3) (3)Или 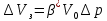 (4) (4)Где 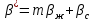 (5) (5)Коэффициент 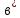 называется коэффициентом упругоемкости пласта. На основании формулы (4) коэффициент упругоемкости пласта называется коэффициентом упругоемкости пласта. На основании формулы (4) коэффициент упругоемкости пласта 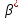 численно равен изменению упругого запаса жидкости в единице объема пласта при изменении пластового давления в нем на единицу. численно равен изменению упругого запаса жидкости в единице объема пласта при изменении пластового давления в нем на единицу.Если формулы (3) или (4) относить к разрабатываемому в условиях замкнуто-упругого режима нефтяному месторождению, то под 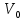 следует понимать объем пласта, в котором к данному моменту времени произошло изменение давления на величину следует понимать объем пласта, в котором к данному моменту времени произошло изменение давления на величину 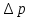 , при этом , при этом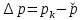 (6) (6)где 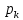 - начальное пластовое давление; - начальное пластовое давление; 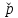 - средневзвешенное по объему возмущенной части пласта - средневзвешенное по объему возмущенной части пласта 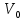 давление. давление.Вычислить средневзвешенное пластовое давление 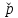 можно, если известна геометрия возмущенной части пласта и конкретное распределение давления в ней. можно, если известна геометрия возмущенной части пласта и конкретное распределение давления в ней.Дифференцируя равенство (4), получим: 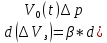 ], ],С другой стороны, изменение упругого запаса жидкости в пласте за время dt равное объему отобранной жидкости: 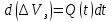 , ,где 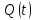 -дебит всех скважин, эксплуатирующих данную нефтяную залежь. -дебит всех скважин, эксплуатирующих данную нефтяную залежь.Приняв правые части двух последних равенств, получим дифференциальное уравнение истощения нефтяной залежи в условиях замкнуто упругого режима 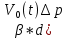 = = 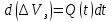 (7) (7)1.3 Методика расчета падения пластового давления по времени при режиме постоянного отбора жидкости Пусть в неограниченном горизонтальном пласте постоянной толщины И имеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пласте одинаково и равно 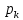 В момент времени t =0 скважина пущена в эксплуатацию с постоянным объемным дебитом В момент времени t =0 скважина пущена в эксплуатацию с постоянным объемным дебитом 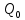 . В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Распределение давления в пласте (в любой его точке в любой момент времени) p (r, t) определяется интегрированием уравнения (8): . В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Распределение давления в пласте (в любой его точке в любой момент времени) p (r, t) определяется интегрированием уравнения (8):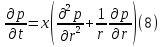 , ,Начальные и граничные условия задачи следующие p(r,t)= 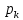 при t=0; при t=0;p(r,t)= 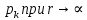 ; ;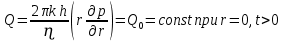 (9) (9)Последнее условие запишем в виде 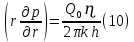 , ,Так же, как в предыдущем случае, проведем анализ размерностей. Искомое распределение давления в пласте зависит от пяти определяющих параметров: r, t, x, 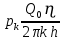 , размерности которых следующие: , размерности которых следующие:[r]=L; [t]=T; [x]=L2T-1; [ 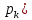 =[p]; [ =[p]; [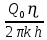 ,]=[p], ,]=[p],где [р]- размерность давления. Тогда давление, приведенное к безразмерному виду, Р=p/ 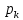 зависит от двух безразмерных параметров (так как из пяти параметров три имеют независимые размерности (r, t, зависит от двух безразмерных параметров (так как из пяти параметров три имеют независимые размерности (r, t,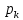 ): n = 5, k = 3, n-k = 2. ): n = 5, k = 3, n-k = 2.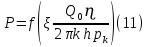 , ,Где 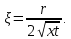 , ,Таким образом задача автомодельна и уравнение (8) можно свести к обыкновенному. Продифференцировав (11), найдем аналогично предыдущему: 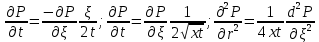 , ,Подставив эти выражения в уравнение (8), получим обыкновенное дифференциальное уравнение вида 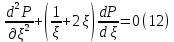 , ,которое нужно проинтегрировать при условиях, полученных из (9):P=1 при 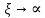 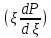 = = 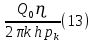 Воспользуемся подстановкой 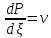 , ,тогда вместо уравнения (12) будем иметь 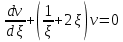 , ,Или 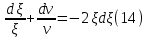 , ,Проинтегрировав (14), получим: 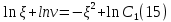 , ,Где 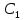 - постоянная интегрирования. - постоянная интегрирования.Потенцируя (15), получим: 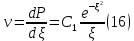 , ,Проинтегрировав (16), и учтя первое из условий (13), получим: 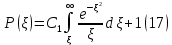 , ,Умножая равенство (16) на 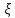 устремляя устремляя 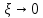 и используя второе условие (13), найдем, что и используя второе условие (13), найдем, что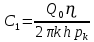 , ,Тогда из (17) получим: 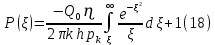 , ,Интеграл в последней формуле легко свести к табличному следующей подстановкой: 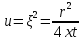 , ,Тогда 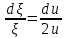 , ,Перейдя также от безразмерного давления P к размерному р =P 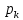 получим: получим: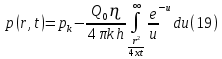 , ,Интеграл в формуле (19) называется интегральной показательной функцией, которая табулирована и обозначается 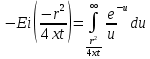 , ,Следовательно, давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется по формуле 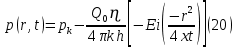 , ,Формула (20) получила название основной формулы теории упругого режима фильтрации. Она имеет широхое практическое применение и, в частности, используется при интерпретации результатов исследования скважин, в расчетах распределения давления при фильтрации упругой жидкости и т. д. Интегральную показательную функцию можно представить в виде ряда 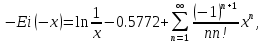 ; ;который сходится при всех значениях х 0 < х< 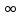 . При изменении аргумента х от 0 до . При изменении аргумента х от 0 до 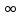 функция функция 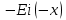 быстро убывает от быстро убывает от 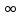 до 0. График этой функции приведен на рис.1. При малых значениях х суммой ряда можно пренебречь, тогда до 0. График этой функции приведен на рис.1. При малых значениях х суммой ряда можно пренебречь, тогда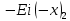 , ,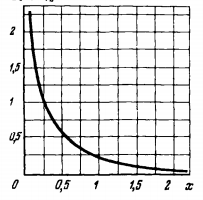 Рис. 1. График интегральной показательной функции 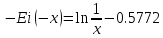 , ,При этом погрешность не превосходит: 0,25% если x =[ 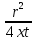 ] ≤0,01; ] ≤0,01;1% если x ≤ 0,03; 5,7% если х ≤ 0,1; 9,7% если х ≤ 0,14. Следовательно, для значений 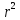 /(4xt) ≤ 1 давление можно определять по формуле /(4xt) ≤ 1 давление можно определять по формуле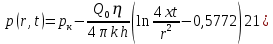 , ,Из формулы (21) выводим Q(t) формула для определения изменения дебита при постоянной депрессии. пластовый интегральный нефть 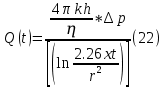 , ,2. Расчетная часть
2.1 Расчета упругого запаса жидкости в пласте 1) Объем рассматриваемой нефтяной залежи 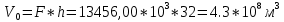 , ,2) Объем нефти без учета сжимаемости 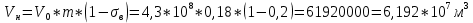 , ,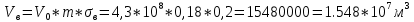 , ,3) Коэффициент β* с учетом сжимаемости воды нефти и породы: 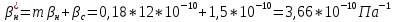 , ,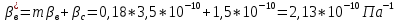 , ,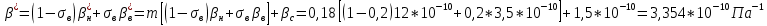 , ,4) Средневзвешенное пластовое давление 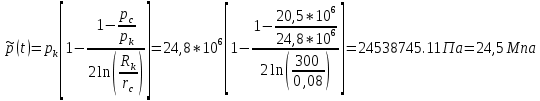 , ,5) Изменение упругого запаса в пласте при учете сжимаемости воды, нефти и породы 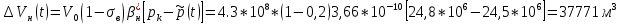 , ,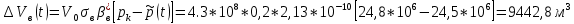 , ,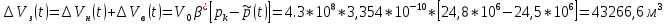 , ,2.2 Расчет падения пластового давления по времени при режиме постоянного отбора жидкости 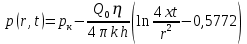 , ,При t=86400 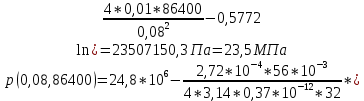 , ,При t=86400 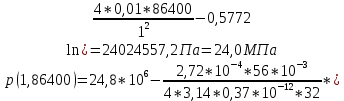 , ,При t=86400 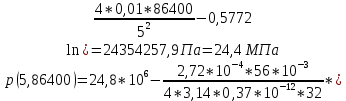 , ,При t=4320000 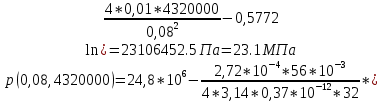 , ,При t=4320000 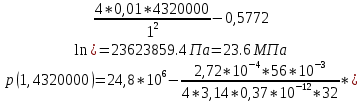 , ,При t=4320000 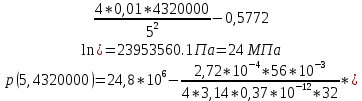 , ,При t=25920000 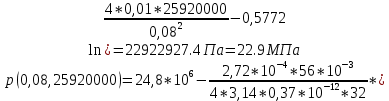 , ,При t=25920000 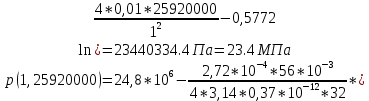 , ,При t=25920000 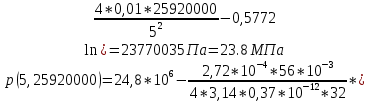 , ,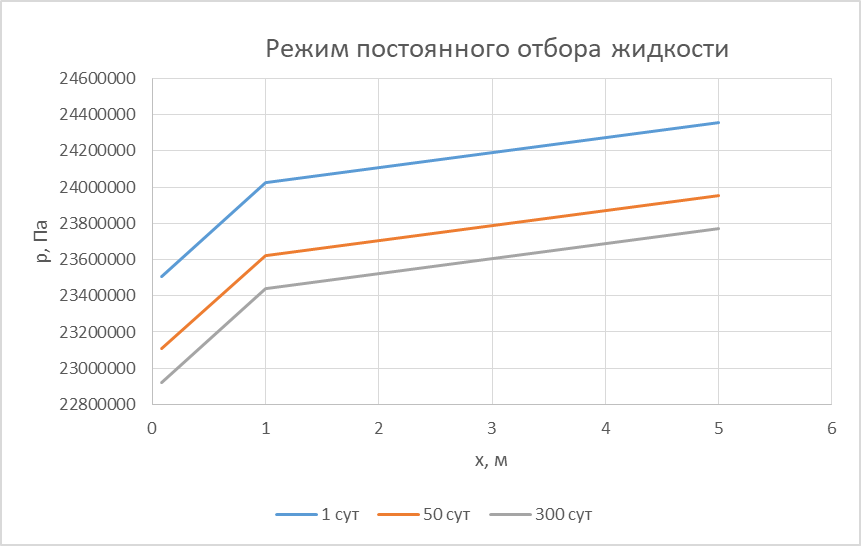 Рис. 2 Вывод: Эти кривые имеют такой же характер, как и при установившейся фильтрации – они очень крутые в близи скважины. При изменении значения r, изменяется давление в данной точке с течением времени, т.е. давление будет понижаться 2.3 Расчет динамики отбора жидкости и пластового давления при режиме постоянной депрессии на пласт 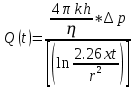 , ,При t=1сут 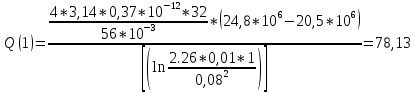 , ,При t=50сут 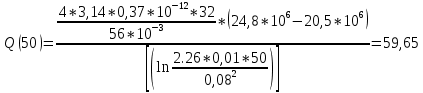 , ,При t=300сут 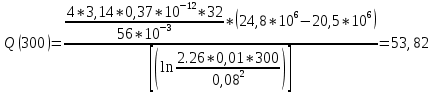 , ,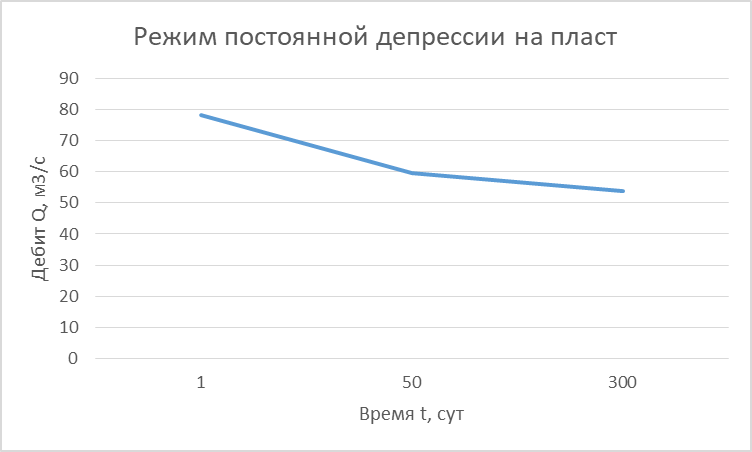 Рис. 3 Вывод: Из графика видно, что стечением времени дебит уменьшается, т.е. количество нефти, извлеченного из пласта за некоторый промежуток времени, равно изменению запасов нефти в пласте, т.к. пласт замкнут,то запасы ограничены и не пополняются из вне. Список использованной литературы 1. Подземная гидромеханика: Учебно-методическое пособие / сост. С.Ю. Борхович, И.В. Пчельников, С.Б. Колесова – Ижевск: Издательский центр « Удмуртский университет» 2017 2. Основы нефтегазопромыслового дела: Авторы В. Д. Гребнев, Д. А. Мартюшев Г. П. Хижняк 3. Подземная гидромеханика Басниев 1993: Авторы Басииев К. С, Кочина И. Н., Максимов В. М 4. Нефтегазовая гидромеханика: Учебное пособие для вузов. — М.-Ижевск: Институт компьютерных исследований, 2005: Авторы Басниев К. С., Дмитриев Н. М., Розенберг Г.Д. |

 4
4
 5
5 6
6 9
9 10
10 11
11