ekonomicheskiy-rost курсовая макроэкономики. 1. теория экономического роста 5 Понятие экономического роста 5

• Название: 1. теория экономического роста 5 Понятие экономического роста 5
• Дата: 16.11.2022
• Размер: 87.58 Kb.
• Имя файла: ekonomicheskiy-rost курсовая макроэкономики.docx
• Тип: Документы; #792428
• страница: 2 из 3

2.2. Неокейнсианская модель

Неокейнсианскими называют модели роста, в которых кейнсианские предпосылки и методы анализа экономической конъюнктуры в коротком периоде используются для описания экономических процессов в длинном периоде.

Эти модели возникли как развитие и критическая переработка кейнсианской теории макроэкономического равновесия⁸.

Данные модели были сформулированы (почти одновременно) американским экономистом польского происхождения Е. Домаром и английским экономистом Р. Харродом. Полученные ими результаты оказались настолько близки между собой, что их впоследствии стали именовать в науке как модель Харрода — Домара. Однако поскольку в моделях есть свои особенности, то рассмотрим каждую из них в отдельности, а в заключение обратим внимание на то, что их объединяет.

Е. Домар открыто признавал, что его модель следует в русле кеинсианской традиции и покоится на кейнсианском фундаменте, но в то же время подчеркивал свой вклад в развитие кеинсианской теории в той части, которая касается роли инвестиций в экономической динамике.

Для Дж. Кейнса инвестиции были важны как расходы (купля), которые рассматривались односторонне, без связи с предложением (продажей).

У Е. Домара же инвестиции являются фактором не только образования доходов, но и создания мощностей, и, следовательно, развития производства, и предложения товаров.

Таким образом, Е. Домар исходил из сбалансированного состояния экономики, когда национальный доход, представляющий общий спрос, равняется производственным мощностям, которые, в свою очередь, представляют общее предложение.

Далее Е. Домар поставил вопрос: как должны расти инвестиции, чтобы темп прироста дохода равнялся темпу прироста производственных мощностей? И для ответа на этот вопрос он составил три уравнения:

• 
  уравнение предложения;
  
• 
  уравнение спроса;
  
• 
  уравнение, выражающее равенство предложения и спроса.
  

Уравнение предложения показывает, какой прирост производственных мощностей (производства) создают инвестиции.

Прирост производства ∆Q, получаемый за счет созданных производственных мощностей, можно определить путем умножения общих капиталовложений I на их среднюю производительность β:

Символ β, характеризующий влияние инвестиций на развитие производства, получил название капиталоотдачи (увеличение занятости рабочей силы, научно-технический прогресс, совершенствование организации производства и т. д.). Так, если для производства продукции на 1 млрд. руб. в год требуется 4 млрд. руб. капитала, то (3 составит четверть, или 25%, в год. Следовательно, выражает величину нового продукта, созданного единицей инвестиций.

Уравнение спроса показывает, на какую величину должен возрасти спрос, чтобы занять дополнительные мощности. Согласно теории мультипликатора, при любой предельной склонности к сбережению, а прирост национального дохода ∆Y является результатом мультипликационного воздействия дополнительных инвестиций ∆I:



где — мультипликатор.

Если сравнить уравнение предложения и уравнение спроса то нетрудно заметить, что в уравнении предложения выступают общие инвестиции, в то время как в уравнении спроса — только прирост инвестиций по сравнению с предыдущим периодом. Это объясняется тем, что прирост производства обеспечивается производительностью всего капитала, тогда как прирост дохода — лишь мультипликационным воздействием дополнительных капиталовложений.

Уравнение равенства темпов прироста дохода и производственных мощностей достигается, когда



Решением этого уравнения устанавливается, что



В левой части уравнения стоит годовой темп роста инвестиций, которые для поддержания полной занятости с помощью увеличения производственных мощностей должны расти с годовым темпом αβ. Доход должен расти с тем же темпом.

Из полученной формулы следует, что сбалансированный темп роста инвестиций является произведением склонности к сбережениям и степени 26 производительности инвестиций. Например, если бы склонность к сбережениям α = 20%, а производительность капитала β = 33%, то норма сбалансированного роста инвестиций должна была бы составлять 6,6%:



Таким образом, модель Домара позволяет определить тот темп, с которым должны постоянно расти инвестиции. Этот темп находится в прямой зависимости от доли сбережений в национальном доходе (предельной склонности к сбережениям) и средней эффективности инвестиций.

Отсюда следовал важный вывод для экономической политики: только постоянно растущая аккумуляция капитала (рост инвестиций) обеспечивает в масштабе общества динамичное равновесие между совокупным спросом и совокупным предложением. Для поддержания сбалансированного роста инвестиций государство может воздействовать на долю сбережений (накопления) в национальном доходе или на темпы технического прогресса (производительность капитала).

Модель Р. Харрода сходна с моделью Е. Домара, однако у нее есть свои особенности.

Целью модели является исследование траектории роста экономики. Поэтому ее основу составляет теория акселератора, позволившая определить отношение прироста инвестиций к вызвавшему его приросту дохода.

Принцип акселератора показывает, что возросшие доход и спрос, в свою очередь, ускоряют инвестиционный процесс, Это означает, что новые капиталовложения — функция прироста дохода, умноженного на коэффициент акселерации δ:



Коэффициент акселерации — техническая величина, зависящая от типа технического прогресса:

• 
  при капиталоемком техническом прогрессе, требующем больших объемов капитала, значение 5 растет;
  
• 
  при техническом прогрессе, экономящем капитал (капиталосберегающий тип), значение б становится меньше.
  

При создании модели экономического роста Р. Харрод ввел в анализ три уравнения:

• 
  уравнение фактического темпа роста:
  
• 
  уравнение гарантированного темпа роста;
  
• 
  уравнение естественного темпа роста.
  

Уравнение фактического темпа роста — исходное уравнение модели Р. Харрода. Оно показывает, какой должна быть доля сбережений в национальном доходе, чтобы обеспечить накопление части прироста продукции, идущей на производственные цели:

Gc = S

G – фактический прирост общего выпуска за какой-либо период, например за год: G = ∆Y/Y;

c - соотношение «капитал-выпуск» (коэффициент капиталоемкости): c = I/∆Y;

s - доля сбережений в национальном доходе или склонность к сбережению: s=S/Y.

Уравнение гарантированного темпа роста выражает равновесие непрерывного поступательного движения, т. е. прогнозируемую линию развития, на которую настраиваются предприниматели и которой они в целом удовлетворены:

G_wcr = s

Р. Харрод считал, что гарантированный (warranted) темп роста G_w является линией динамического равновесия. Вместе с тем cr (требуемый коэффициент капиталоемкости) также является категорией динамического равновесия: он выражает потребность в новом капитале, деленную на прирост выпуска продукции, для обеспечения которого требуется этот новый капитал.

Сравнивая оба уравнения, он отмечает, что на практике фактический темп роста всегда выше или ниже гарантированного.

Вместо приспособления фактического темпа развития производства к равновесному на практике имеет место обратная тенденция — к все большему удалению производства от линии динамического равновесия либо в сторону повышения, либо в сторону понижения. Это дало основание Р. Харроду сделать вывод о том, что рыночная экономика "балансирует на острие ножа", что ей внутренне присуща динамическая нестабильность.

Уравнение естественного темпа роста в модели Р. Харрода имеет следующий вид:

G_ncr = или ≠ s

где G_n —максимально возможный темп движения экономики при полном использовании ресурсов.

Для поддержания такого темпа роста в экономике может не хватить сбережений, поэтому в уравнении естественного темпа роста предусматривается отсутствие обязательного равенства между левой и правой частями.

В ходе анализа Р. Харрод пришел к выводам, аналогичным тем, которые получил Е. Домар. Часто их модели, как уже отмечалось, объединяют в одну модель Харрода-—Домара. Из нее следует, что при данных технических условиях производства темп экономического роста определяется величиной предельной склонности к сбережению, а динамическое равновесие в рыночной системе по своей природе неустойчиво и для его поддержания в условиях полной занятости требуются активные и целенаправленные действия государства.

Ограниченность модели Харрода—Домара определялась не только предпосылками ее анализа, но и историческими условиями: она более или менее адекватно описывала реальные процессы экономического роста в 1930-е гг. и в послевоенный (восстановительный) период, когда главные усилия в развитии производства сосредотачивались на увеличении инвестиций и создании новых производственных мощностей при постоянстве капиталоемкости (капиталоотдачи). В более поздний период (вторая половина 50-х — 70-е гг.) перспективы развития производства во все большей мере стали определяться воздействием на него качественных изменений, что нашло отражение в неоклассических теориях экономического роста.

2.3. Неоклассическая модель

В центре неоклассического направления стоит идея равновесия, основанного на оптимальной рыночной системе, рассматриваемой как совершенный саморегулирующийся механизм, позволяющий наилучшим образом использовать все производственные факторы не только отдельному экономическому субъекту, но и экономике в целом.

В реальной экономической жизни общества это равновесие нарушается. Однако моделирование равновесия позволяет найти отклонение реальных процессов от идеала.

Основными характеристиками неоклассических моделей экономического роста являются⁹:

• 
  предположение о функционировании экономики в условиях совершенной конкуренции, обеспечивающей гибкую систему цен и равенство цен факторов производства их предельной производительности;
  
• 
  отсутствие функции совокупного спроса, поскольку гибкая система цен постоянно приравнивает объем совокупного спроса к объему совокупного предложения;
  
• 
  отсутствие функции инвестиций, так как при равновесии на рынке благ I = S;
  
• 
  представление технологии в виде производственной функции с взаимозаменяемыми факторами производства и постоянным эффектом масштаба.
  

Американцы Чарльз Кобб и Пол Дуглас в 20-е гг. ХХ века разработали многофакторную модель экономического роста, получившую название производственной функции или модели Кобба-Дугласа.

Она показывает, что объем совокупного продукта при данном уровне технологий зависит от двух факторов: капитала и трудовых ресурсов.

У = F (K, L)

где У - объем совокупного продукта; K- капитал; L- трудовые ресурсы.

В последующем производственная функция была усовершенствована. В частности, при ее расчете предлагалось учитывать фактор времени, поскольку уровень технологий постоянно повышается. Впервые расчет производственной функции с учетом фактора времени осуществил Ян Тинберген. В результате производственная функция приняла следующий вид:

У (t) = A(t) F [Ka(t), LP(t), Ny (t)]

где У (t) - объем производства за период времени t; A (t) - коэффициент, отражающий развитие научно-технического прогресса за период времени t; Ka(t), Lfi(t), Ny (t) - затраты соответственно капитала, труда, природных ресурсов за период времени t; а, в, y - коэффициенты эластичности производства соответственно по капиталу, труду, природным ресурсам.

Они показывают, как возрастает объем производства, вызванный приростом на 1% соответствующих факторов экономического роста.

Затем лауреат Нобелевской премии американец Роберт Солоу модифицировал производственную функцию Кобба-Дугласа путем ввода еше одного фактора — уровня развития технологий.

При этом он исходил из того, что изменение технологии приводит к одинаковому увеличению K и L:

Q = T * F (K, L),

Где Q – выпуск продукции; K – основной капитал; L – вложенный труд (в виде заработной платы); T – уровень развития технологий; F(K, L) – производственная функция Кобба-Дугласа.

Если доля капитала в выпуске продукции измеряется такими показателями, как капиталовооруженность (или фондовложенность) на одного работающего, и фондоотдача (количество продукции на одну денежную единицу производственных фондов); доля труда — на основе производительности труда, то вклад технического прогресса представляется как остаток после вычета из прироста выпуска продукции доли, полученной за счет прироста труда и капитала. Это так называемый остаток Солоу, который выражает долю экономического роста за счет технического прогресса, или «прогресса в знаниях».

Предпосылками анализа в модели Р. Солоу является: взаимозаменяемость труда и капитала (как в модели Кобба-Дугласа), убывающая предельная производительность капитала; постоянная отдача от масштаба, постоянная норма выбытия основных фондов; отсутствие инвестиционных лагов.

При неизменной численности занятых динамика объема выпуска зависит от объема капитала (в данном случае в расчете на одного занятого, т.е. капиталовооруженности (фондовооруженности). В свою очередь, объем капитала меняется под воздействием инвестиций и выбытия основных фондов. Размеры инвестиций зависят от нормы сбережения, с ростом которой они увеличиваются, превышая выбытие капитала, и фондовооруженность возрастает. С ростом фондовооруженности темп роста инвестиций (сбережений) естественно падает. Инвестиции увеличивают запас капитала, выбытие уменьшает. Уровень запаса капитала, при котором инвестиции равны его выбытию, есть равновесный уровень фондовооруженности труда. При достижении этого экономика будет находиться в состоянии долгосрочного равновесия.

В случае, когда рост становится сбалансированным, его дальнейший темп зависит только от роста населения и технического прогресса.

Рост населения при том же объеме капитала снижает фондовооруженность. Привлекаемые при этом инвестиции должны не только покрыть выбытие капитала, но и обеспечить капиталом новых рабочих в прежнем объеме.

Для того чтобы фондовооруженность оставалась постоянной и при роете населения, капитал должен возрастать таким же темпом, что и население: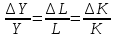



Технологический прогресс в модели Солоу является единственным условием непрерывного повышения уровня жизни, так, как только при его наличии наблюдается устойчивый рост фондовооруженности и выпуска продукции в расчете на одного занятого, т.е. фондоотдачи.

Однако по мере роста фондовооруженности (К/Д) количество продукции на одного занятого (Q/L) возрастает в меньшей степени, чем фондовооруженность, так как падает предельная производительность капитала.

Обозначим производство продукции на одного занятого (Q/L) q, количество капитала на одного работающего (K/L) через к (капитало- или фондовооруженность), тогда производственная функция примет следующий вид:

q = TF(k)

Как видно из рис. 1, по мере роста фондовооруженности происходит рост   (количество продукции на одного занятого), но оно возрастает в меньшей степени, так как падает предельная производительность капитала (фондоотдача), согласно закону убывающей отдачи.

В модели Солоу объем производства   определяется инвестициями   и потреблением  . Предполагается, что экономика носит закрытый от мирового рынка характер и отечественные инвестиции   равны национальным сбережениям, или объему валового сбережения   т.е.  .



Рис 1 Производственная функция в расчете на душу населения

В настоящее время в западных странах получила распространение концепция «экономического развития без роста» или «нулевого экономического роста». Это связано, с одной стороны, с тем, что на основе НТР уже достигнут высокий уровень подушевого производства, а с другой — значительно уменьшились темпы роста населения. Кроме того, сторонники этой концепции считают, что экономический рост приводит к нарушению биосферы жизни человека и ограничен в силу недостаточности сырьевых и топливных ресурсов планеты.

В частности, группа исследователей под руководством Дениса и Донеллы Медоуз предупреждают об опасности «глобальной катастрофы», которая грозит человечеству вследствие технического прогресса, разрушающего окружающую среду.

Полемизируя с ними, другие специалисты и ученые (известный теоретик и историк экономической мысли, российский ученый Ю. Ольсевич; германский экономист и политик Э. Пестель и др.) считают, что нужно изменить тенденции роста, ввести ограничения на использование природных ресурсов, загрязнение среды. С помощью современных технологий вполне можно смягчить противоречия между растущими потребностями и ограниченными ресурсами.