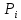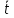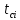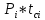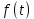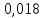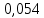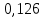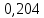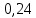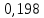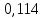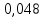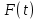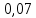ргр. 1. Упорядочивание выборки (массива) Составляем сводную таблицу
 Скачать 0.9 Mb. Скачать 0.9 Mb.
|
 1. Упорядочивание выборки (массива) 1. Упорядочивание выборки (массива)Составляем сводную таблицу Таблица 1
2. Составление статистического ряда информации. Находим количество интервалов: 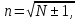 где N - общее количество показателей N=70 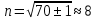 Находим длину интервала: 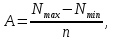 где 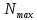 - максимальная наработка, а - максимальная наработка, а 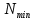 - минимальная наработка. - минимальная наработка.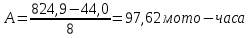 Сами интервалы будут иметь вид: 1. 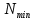 ... ... 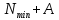 2. 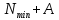 ... ... 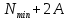 3. 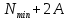 ... ...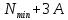 . . 8. ... ... 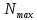 . . Также найдем середину каждого i-го интервала: 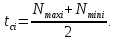 Определим опытную частоту показателя надежности 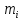 - сколько чисел массива попало в i-й интервал. - сколько чисел массива попало в i-й интервал.Определим опытную вероятность для каждого i-го интервала: 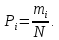 Отсюда находим накопленную опытную вероятность 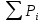 Полученные результаты заносим в таблицу 2. Таблица 2
Определим среднее значение показателя надежности: 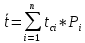 Тогда 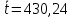 Определим среднее квадратичное отклонение: 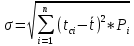 Тогда 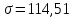 3. Проверка информации на выпадающие точки Нижняя точка: 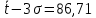 Верхняя точка: 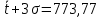 По результатам проверки 2 числа из выборки не попадают в интервал : 44,0 и 824,9. Поэтому производим расчет по 2 разделу без этих чисел, т. е. N=68.  2.1 Составление статистического ряда информации. Находим количество интервалов: 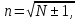 где N - общее количество показателей N=68 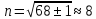 Находим длину интервала: 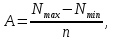 где 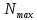 - максимальная наработка, а - максимальная наработка, а 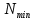 - минимальная наработка. - минимальная наработка.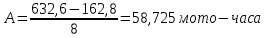 Остальные величины также считаем по 2 разделу. Сводим полученные данные в таблицу 3. Таблица 3
Определим среднее квадратичное отклонение: 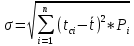 Тогда 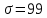  3.1 Проверка информации на выпадающие точки Нижняя точка: 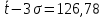 Верхняя точка: 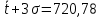 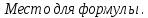 По результатам проверки все значения выборки попадают в интервал. 4. Выполнение графического изображения опытного распределения показателя надежности. Гистограмма накопленных опытных вероятностей 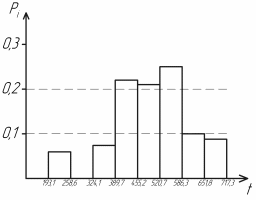 Полигон распределения ресурсов  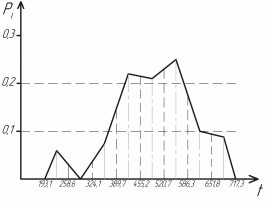  Кривая накопленных опытных вероятностей 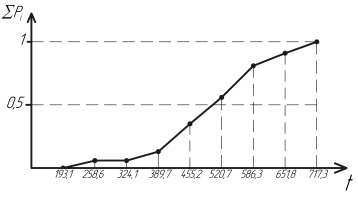 5. Определение коэффициента вариации 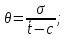 где c - смещение рассеяния показателя надежности 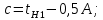 где 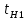 - начало первого интервала - начало первого интервала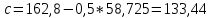 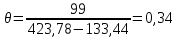 6. Выбор теоретического закона распределения для выравнивания опытной вероятности 6.1. Использование для выравнивания распределения опытной информации закона нормального распределения. Дифференциальная функция распределения: 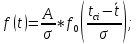 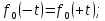 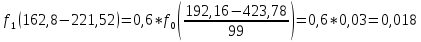 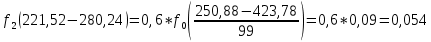 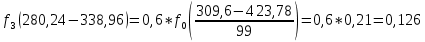 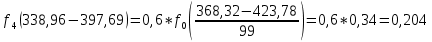 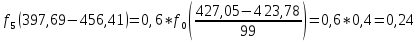  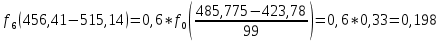 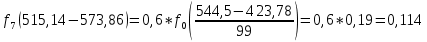 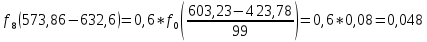 Интегральная функция распределения: 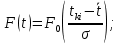 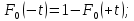 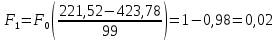 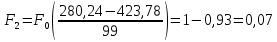 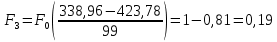 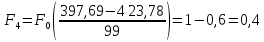 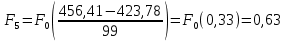 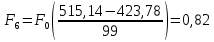 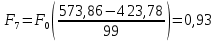 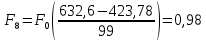 Сводим полученные данные в таблицу 4 Таблица 4
6.2. Использование для выравнивания опытной информации для закона Вейбула. Используя таблицу параметров и коэффициентов распределения Вейбула находим эти коэффициенты при 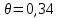 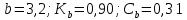 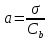 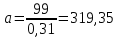  Дифференциальная функция распределения: Дифференциальная функция распределения: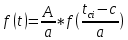 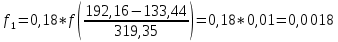 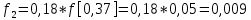 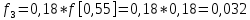 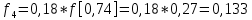 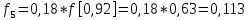 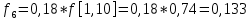 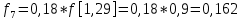 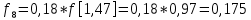 Интегральная функция распределения: 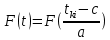 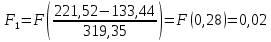 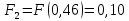 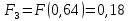 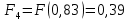 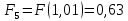 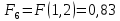 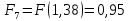 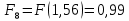 Сводим полученные данные в таблицу 5 Таблица 5
7. Оценка совпадения опытного и теоретического законов распределения показателей надежности по критерию согласия. Критерия Пирсона. 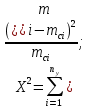 где 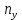 - количество интервалов укрупненного интервала; - количество интервалов укрупненного интервала;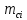 - теоретическая частота в i-ом интервале; - теоретическая частота в i-ом интервале;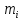 - опытная частота в i-ом интервале. - опытная частота в i-ом интервале.Условия для создания укрупненного интервала: 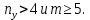  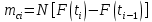 Сводим все расчеты в таблицу 6 Таблица 6
Для закона нормального распределения: 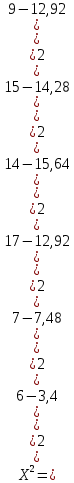 Для закона распределения Вейбулла: 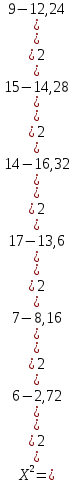 Выбираем меньшее значение, в данном случае при законе нормального распределения 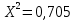 8. Определение доверительных границ рассеивания одиночного и среднего значений показателей надежности при законе нормального распределения. Доверительный интервал рассеивания одиночных показателей надежности: 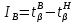 Нижняя доверительная граница: 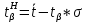 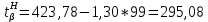 Верхняя доверительная граница: 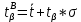 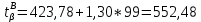 Доверительный интервал: 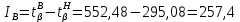 Доверительный интервал рассеивания средних значений показателей надежности: 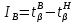 Нижняя доверительная граница: 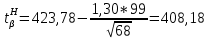 Верхняя доверительная граница: 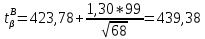 Доверительный интервал: 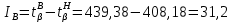 Удельная относительная ошибка показателя: 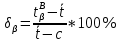 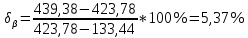  Вывод: пользуясь статистическим методом исследования надежности, Вывод: пользуясь статистическим методом исследования надежности, просчитали данную выборку опытных значений. Выполнили графическое изображение опытного распределения показателя надежности( гистограмма, полигон и кривая накопленной опытной вероятности). Провели оценку совпадения опытного и теоретического законов распределения показателя надежности по критерию согласия.  Дифференциальная функция Вейбулла: 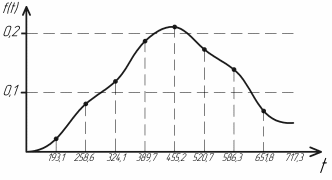 Интегральная функция Вейбулла: 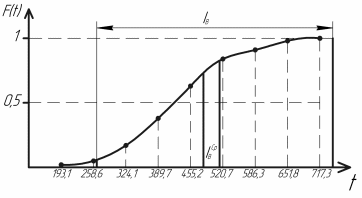 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||