геометрия пирамида. 1. в правильной треугольной пирамиде sabc медианы основания abc пересекаются в точке Площадь треугольника abc равна 9 объем пирамиды равен Найдите длину отрезка 2
 Скачать 121.1 Kb.
|
|
1. 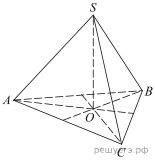 В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке  П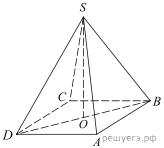лощадь треугольника ABC равна 9; объем пирамиды равен 6. Найдите длину отрезка  2.  В правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина,   Н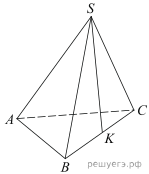айдите длину отрезка  3.  В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC. 4. 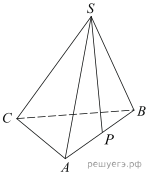 В правильной треугольной пирамиде SABC P – середина ребра AB, S – вершина. Известно, что BC=5, а SP=6. Найдите площадь боковой поверхности пирамиды. 5. 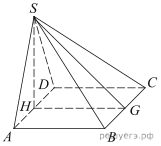 Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды. 6. 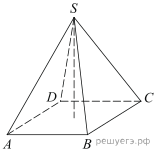 В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем. 7. 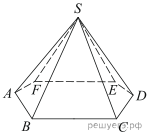 Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза? 8. 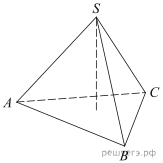 Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен  9. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна 10. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды. 11.  Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?12. 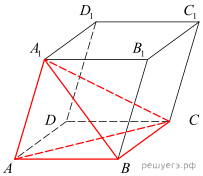 Объем параллелепипеда  ра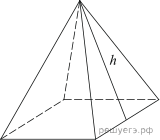вен 9. Найдите объем треугольной пирамиды  13.  Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды. 14.  Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.15. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S — вершина,   Найдите длину отрезка  |