Курсовой проект. 1 Выбор схемы расположения тросов на опоре. Определение габаритного весового и ветрового пролетов
 Скачать 65.84 Kb. Скачать 65.84 Kb.
|
|
Содержание
Введение Воздушные линии электропередач предназначены для передачи электроэнергии на расстояния. Основными элементами воздушных линий являются провода и тросы, опоры, изоляторы, линейная арматура и т.д. В курсовом проекте необходимо произвести расчет линии электропередач 100 кВ в анкерном пролете на механическую прочность. Напряжения в проводе 240/56 и тросе АС70/72 не должно превышать допустимых при любых погодных условиях, возможных в данной местности. Стрелы провеса провода и троса также не должны превышать допустимых значений в любом режиме. Проектирование механической части воздушных линий ЛЭП ставит своей главной задачей обеспечение высокой надежности работы ВЛ в естественных природных условиях. Это проектирование включает следующие основные этапы: Выбрать схему расположение провода на опоре, если известны: номинальное напряжение воздушной линии электропередачи; материал опор; количество цепей; районы по ветру и гололеду, где будет проходить трасса линий; минимальное, максимальное и среднегодовое значение температуры окружающего воздуха. Необходимо так же определить значения габаритного, весового и ветрового пролетов. Расчет механических нагрузок на элементы ВЛ; выбор элементов ВЛ; Цель выполнения курсового проекта является освоение основ проектирования механической части ВЛ. 1 Выбор схемы расположения тросов на опоре. Определение габаритного весового и ветрового пролетов При толщине стенки гололеда до 20мм провода на опоре могут располагаться по треугольнику, а при толщине стенки гололеда более 20 мм предпочтении следует отдавать горизонтальному расположению проводов. Для двух цепных линий (при вертикальном расположении проводов) расположение проводов в виде бочки, прямой или обратной елки необходимо выбирать схему, исходя из минимума суммарной длины траверса на опоре. Длина габаритного пролета, т.е. такая длина пролета, при которой соблюдается допустимый габарит от нижней точки провода до земли, определяется по формуле 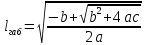 Где 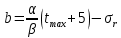 ; ; 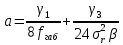 ; ; 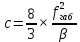 ; ;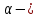 коэфициент температурного расширения провода, коэфициент температурного расширения провода, 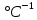 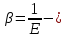 коэффициент упругого удлинения провода, коэффициент упругого удлинения провода, 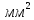 /даН; /даН;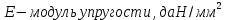 tmax – максимальная температура, °С; σг – допустимое напряжение в материале провода при наибольшей механической нагрузке, даН/мм2; γ1 – удельная механическая нагрузка от собственного веса провода, даН/м×мм2 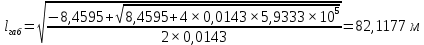 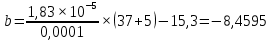 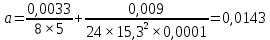 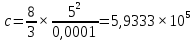
удельная механическая нагрузка от собственного веса провода γ1 и веса гололеда γ2 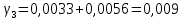 f_габ=h_n-λ-h_доп – габаритная стрела провеса провода, м; hn – расстояние от земли до нижней траверсы, м; может быть принято равным 12 – 15; м соответственно для линий напряжением до 110 кВ; λ – длина гирлянды изоляторов; принимается равной 1,0 м соответственно для линий номинальным напряжением 110 кВ; hдоп – допустимое расстояние (габарит от земли), принимается равным 6,0 м соответственно для линий 110 кВ. Удельная механическая нагрузка от собственного веса и гололеда вычисляется как
где G0 – вес единицы длины провода; даН/м; Fa, Fc – площадь поперечного сечения алюминиевой и стальной частей провода; d – диаметр провода, мм; b – толщина стенки гололеда, мм. 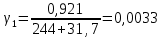 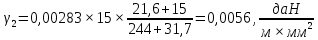 1.1Определение длины весового и ветрового пролетов Весовой пролет определяется только после расстановки опор по профилю трассы, когда известна разность Δh высот точек подвеса проводов на рассматриваемой опоре и смежных опорах. В качестве решения принимается, что длина весового и ветрового пролета равна 1,25 длины габаритного пролета, т.е. 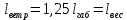 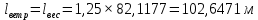 2 Выбор линейной изоляции и арматуры Изоляция для воздушных линий электропередачи выбирается по механической и электрической прочности. Количество m изоляторов в изолирующей подвеске линий напряжением 35–750 кВ определяется по формуле
где λу – удельная длина пути утечки по отношению к наибольшему рабочему напряжению, мм/кВ; для линий напряжением 110-220 кВ она равна соответственно 16 мм/кВ; Uраб – наибольшее рабочее линейное напряжение линии, кВ; при номинальном напряжении 110 кВ оно равно соответственно 126 кВ; lут – длина пути утечки одного изолятора, мм (измеряется расстоянием по поверхности между его шапкой и пестиком); для подвесных стеклянных изоляторов типа ПС 70А она равно соответственно 295 мм. 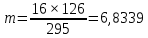 На линиях напряжением 220 кВ с металлическими опорами используется больше на один изолятор, определяемого по формуле (2.1). Длина гирлянды изоляторов определяется умножением количества изоляторов в гирлянде на строительную высоту Н одного изолятора. Для линий 110 кВ она равняется 1,0 м. По условию механической прочности механическая разрушающая нагрузка Рразр на изолятор должна быть больше максимальной из расчетных механических нагрузок нормального и аварийного режимов: 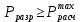 Расчетные нагрузки на изолятор нормального режима определяются по среднегодовым условиям и условиям работы при наличии гололеда на проводах и воздействии ветра:
где 5 и 2,7 – коэффициенты запаса прочности изоляторов в нормальных режимах; γ1 – удельная механическая нагрузка на провод от собственной массы провода, даН/ммм2 (формула (1.2)); lвес – длина весового пролета, м; n – количество проводов в фазе линии; gи– масса одного изолятора; для изоляторов типа ПС70-А, ПС120-А, ПС160-Б, ПС300-Б она равна 3,4; 5,7; 7,8; 11,5 кг соответственно; 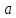 – коэффициент, учитывающий массу линейной арматуры; можно принять равным 1,5; 1,4 и 1,3 для линий напряжением 35, 110, и 220 кВ и выше; – коэффициент, учитывающий массу линейной арматуры; можно принять равным 1,5; 1,4 и 1,3 для линий напряжением 35, 110, и 220 кВ и выше;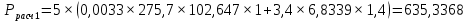 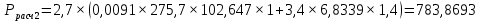 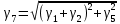 – удельная механическая нагрузка на провод от воздействия собственного веса провода γ1, гололеда γ2 и ветра γ5. – удельная механическая нагрузка на провод от воздействия собственного веса провода γ1, гололеда γ2 и ветра γ5. 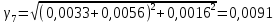 Удельная механическая нагрузка от давления ветра на провод, покрытый гололедом, вычисляется по формуле
где α – коэффициент, учитывающий неравномерность скорости ветра по длине пролета; равен 1,0; 0,76; 0,71; 0,7 при скоростном напоре ветра q до 20, 40 (скорость ветра 25 м/с); 50 (скорость ветра 29 м/с); 58 даН/мм2 и выше (скорость ветра 30 м/с и выше) и определяется для скоростного напора ветра, равного 0,25q; сx = 1,2 – коэффициент лобового сопротивления провода, покрытого гололедом; kl – коэффициент, учитывающий влияние длины пролета на ветровую нагрузку; равен 1,0; 1,05; 1,1; 1,2 соответственно при длине пролета 250; 150; 100; до 50 м; φ – угол между направлением ветра и осью линии; максимальное значение γ5 имеет место при угле φ = 90°, что и принимается в качестве нормативного значения; k – коэффициент, учитывающий возрастание скоростного напора ветра по высоте; при высоте расположения приведенного центра тяжести проводов до 15 м k = 1,0; 20 м – k = 1,25; 40 м – k = 1,50. Нормативное ветровое давление при гололеде, равное 0,25q, должно быть не менее 20, 16 даН/м2 соответственно для линий напряжением до 20 и 330–750 кВ. Для линий напряжением 35220 кВ значение 0,25q округляется до 12 даН/м2. 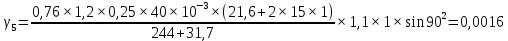 Если провод не покрыт гололедом, то соответствующая удельная нагрузка γ4 определяется как
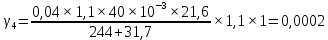 где α' определяется при нормативном скоростном напоре ветра, т. е. при qk; 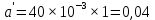 c'x = 1,1 при d ≥ 20 мм и c'x = 1,2 при d < 20 мм. Результирующая нагрузка от воздействия ветра на провод, не покрытый гололедом, определяется как 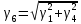 . .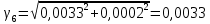 Значение разрушающих нагрузок указывается в типе изоляторов в килоньютонах. Расчетные механические нагрузки на изоляторы в аварийном режиме находятся по формуле
где k1 – коэффициент, учитывающий долю тяжения по проводу, приложенного к изолятору, при обрыве провода Т = эF – нормативное тяжение по проводу, даН; э – допустимое напряжение при среднегодовых условиях, даН/мм2. 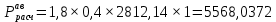 3 Систематический расчет проводов и тросов. Для заданной марки проводов и грозозащитных тросов (см. табл. 1.1) выполнить систематический расчет, т. е. построить зависимости напряжения и стрелы провеса провода от длины пролета при следующих сочетаниях климатических условий (режимов): – максимальной температуре tmax, гололед и ветер отсутствуют; – минимальной температуре , t_ гололед и ветер отсутствуют; – среднегодовой температуре tэ, гололед и ветер отсутствуют; – наибольшей гололедной нагрузке (температура –5 С, максимальная толщина стенки гололеда bmax, ветер отсутствует); – наибольшей ветровой нагрузке (температура –5 С, гололед отсутствует, максимальный скоростной напор ветра q); – наибольшей гололедной нагрузке bmax и скоростном напоре ветра, равном 0,25q или 12 даН/м2 (для линий напряжением 35–220 кВ) и 16 даН/м2 (для линий напряжением 330–750 кВ); температура –5 С; – грозовом режиме (температура +15 С; гололед отсутствует; скоростной напор ветра должен быть не менее 5 даН/м2; при скорости ветра 10 м/с, значение скоростного напора равно 6,25 даН/м2); – монтажном режиме (температура –15 С; гололед отсутствует; скоростной напор ветра 6,25 даН/м2); – расчетной нагрузке от тяжения проводов. Методические указания Зависимость напряжения σ в материале провода или троса от длины пролета l находится по основному уравнению состояния провода в пролете
где γ – удельная механическая нагрузка от действия собственного веса, ветра и гололеда; значение γ различно для отмеченных климатических режимов: для режимов (1–3) – γ1 (формула (1.3)); значение γ4 определяется по формуле (2.5); при скоростном напоре ветра, равном 6,25 даН/м2, γ’4 – по формуле (2.4); 5 – по формуле (2.5); β, – коэффициенты упругого удлинения и температурного расширения (см. тему 1); t – температура, характерная для рассчитываемого режима: 1 – tmax; 2 – t_ ; 3 – tэ; 4–6 – (–5) С; 7 – (+15) С; 8 – (–15); σм – допустимое напряжение в материале провода или троса в одном из режимов (см. табл. 1.1): или наибольшей нагрузки ( тогда 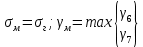 , tм = –5 C; или среднегодовых условий (тогда σм = σэ, γм = γ1; tм = tэ); или наименьших температур (тогда σм = _, γм = γ1; tм = t_); tэ, t_ – среднегодовая и наименьшая температура окружающей среды. , tм = –5 C; или среднегодовых условий (тогда σм = σэ, γм = γ1; tм = tэ); или наименьших температур (тогда σм = _, γм = γ1; tм = t_); tэ, t_ – среднегодовая и наименьшая температура окружающей среды. 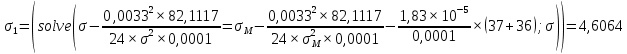 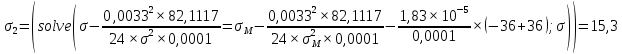 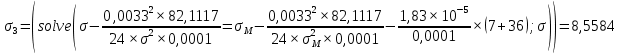 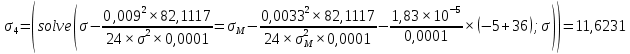 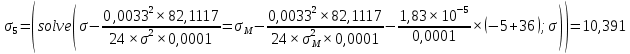 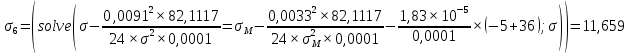 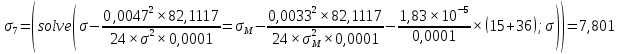 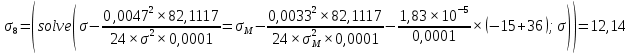 Чтобы правильно подставить значения σм, γм, tм в формулу (3.1), следует вычислить значения трех критических пролетов 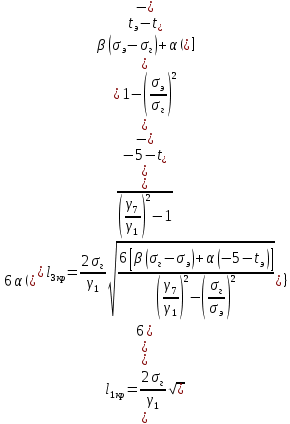 Если окажется, что l1кр < l2кр < l3кр, то при l < l1кр в качестве исходных температурных условий принимается режим минимальных температур, т. е. σм = σ-2; γм = γ1; tм = t_. При l1кр < l < l3кр в качестве исходных температурных условий принимается режим среднегодовых условий, т. е. σм = σэ ; γм = γ1; tм = tэ; при l > l3кр в качестве исходных температурных условий принимается режим наибольших нагрузок, т. е. σм = σг; γм = γ7; tм = –5 С. Если l1кр > l2кр > l3кр, то при l < l2кр в качестве исходных температурных условий принимается режим минимальных температур, т. е. σм = σ_; γм = γ1; tм = t_; при l > l2кр в качестве исходных температурных условий принимается режим наибольших нагрузок, т. е. σм = σг; γм = γ7; tм = –5 С. Если l1кр = Jm, l2кр < l3кр, то при l < l3кр в качестве исходных температурных условий принимается режим среднегодовых условий, т. е. σм = σэ; γм = γ1; tм = tэ; при l > l3кр в качестве исходных температурных условий принимается режим наибольших нагрузок, т. е. σм = σг; γм = γ7; tм = –5 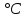 . . Если l3кр = Jm, l1кр < l2кр, то при l < l1кр в качестве исходных температурных условий принимается режим минимальных температур, т. е. σм = σ_ ; γм = γ1; tм = t_; при l > l1кр в качестве исходных температурных условий принимается режим среднегодовых условий, т. е. σм = σэ; γм = γ1; tм = tэ. Если l1кр = Jm, l3кр = Jm, то при любой длине пролета в качестве температурных исходных условий принимается режим среднегодовых условий, т. е. σм = σэ; γм = γ1; tм = tэ. 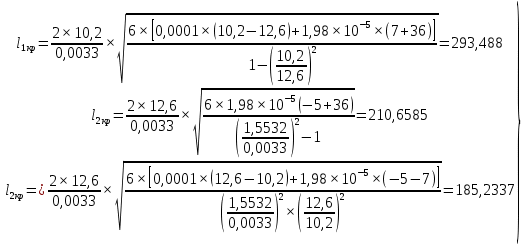 Неполное кубическое уравнение (3.1) решается относительно σ при вариации длины пролета l от минимального значения до габаритной длины пролета, включая точки критических пролетов. Стрела провеса провода вычисляется по выражению
где γ подставляется в соответствии с расчетным режимом климатических условий; σ – найденное по выражению (3.1) напряжение в проводе или тросе. 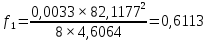 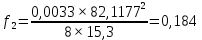 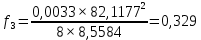 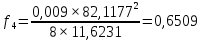 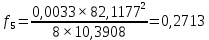 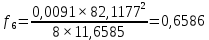 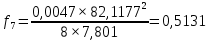 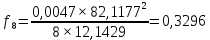 |

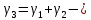
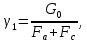
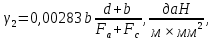
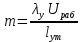
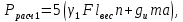
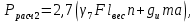
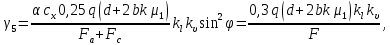
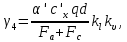
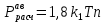 ,
,