Использование элементов комбинаторики на уроках математики. Проектная работа Шахмухамбетова Зауреш. 1 Введение Основная часть
 Скачать 193.4 Kb. Скачать 193.4 Kb.
|
 Содержание 1 Введение………………………………………………………………….. 2 Основная часть 2.1Основное правило комбинаторики……………………………… …… 2.2 Правило сложения………………………………………………........... 2.3 Размещение без повторений…………………………………………... 2.4 Перестановки без повторений………………………………………… 2.5 Сочетания без повторений……………………………………………. 2.6 Размещения с повторениями………………………………………….. 2.7 Сочетания с повторениями……………………………………………. 2.8 Перестановки с повторениями………………………………………... 2.9 Бином Ньютона………………………………………………………... 3.0 Треугольник Паскаля………………………………………………….. 3.1 Практические задания…………………………………………………. 3.2 Вывод…………………………………………………………………… 3.3 Список использованной литературы…………………………………. ВВЕДЕНИЕ Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Слово «комбинаторика» происходит от латинского слова «cоmbinаrе», что в переводе на русский означает – «сочетать», «соединять». Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным. Комбинаторика - ветвь математики, изучающая комбинации и перестановки предметов. Еще комбинаторику можно понимать как перебор возможных вариантов. Комбинаторика возникла в XII веке. Долгое время она лежала вне основной ветви математики. С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов - во время битвы, инструментов - во время работы. Комбинаторные навыки оказались полезными и в часы отдыха. Нельзя точно сказать, когда наряду с состязаниями в беге, метании диска, прыжках появились игры, требовавшие, в первую очередь, умения рассчитывать, составлять планы и опровергать планы противника. Со временем появились различные игры (нарды, карты, шашки, шахматы и т.д.). В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучил, знал выигрышные комбинации и умел избегать проигрышных. Не только азартные игры давали пищу для комбинаторных размышлений математиков. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв, заменах букв с использованием ключевых слов и т.д. Задачи, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называется комбинаторикой. Комбинаторику можно рассматривать как часть теории множеств - любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях Раздел комбинаторики, в котором рассматривается лишь вопрос о подсчете числа решений комбинаторной задачи, теорией перечислений. Комбинаторика как наука стала развиваться в XIII веке параллельно с возникновением теории вероятностей, так как для решения вероятностных задач необходимо было подсчитать число различных комбинаций элементов. Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж. Кардано, Н. Тарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б. Паскалю (1623-1662) и П. Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер. Решение комбинаторных задач развивает творческие способности учащихся. Области применения комбинаторики: учебные заведения (составление расписаний) -сфера общественного питания (составление меню) -лингвистика (рассмотрение вариантов комбинаций букв) -спортивные соревнования (расчёт количества игр между участниками) -агротехника (размещение посевов на нескольких полях) -география (раскраска карт) -биология (расшифровка кода ДНК) -химия (анализ возможных связей между химическими элементами) -экономика (анализ вариантов купли-продажи акций), азартные игры (подсчёт частоты выигрышей) -криптография (разработка методов шифрования) -доставка почты (рассмотрение вариантов пересылки) -военное дело (расположение подразделений) Цель проекта: Помочь в изучении формул комбинаторики и научить применять их при решении задач Задачи проекта:Сформировать навыки применения формул при решении комбинаторных задач Использование элементов комбинаторики на уроках математики В школьном разделе математики изучается перечислительный раздел комбинаторики. Данный раздел рассматривает задачи о перечислении или подсчёте количества различных комбинаций образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п. Количество комбинаций, образованных несколькими операциями над множеством, подсчитывается согласно правилам сложения и умножения. Рассмотрим их поподробнее…. Основное правило комбинаторики: Пусть по условию задачи задано выполнение k действий. Допустим, что первое действие можно выполнить 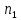 способами, второе действие – n2 способами и так далее до k-го действия, которое можно выполнить nk способами. способами, второе действие – n2 способами и так далее до k-го действия, которое можно выполнить nk способами. Тогда, если выполнение одного действия не влияет на выполнение остальных действий, то задача может быть решена n1·n2·…·nk способами. Другими словами здесь применяется правило умножения: Если элемент х 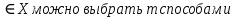 , а элемент y , а элемент y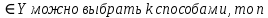 ару «х» и «у» можно выбрать m*k способами. ару «х» и «у» можно выбрать m*k способами.Например: Задача 1. В зоологическом магазине стоят два аквариума с рыбками. В одном плавает пять рыбок, а во втором - шесть. Покупатель решил купить по рыбке из каждого аквариума. Сколькими способами он может это сделать? Решение: Обозначим через 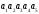 количество рыбок, плавающих в первом аквариуме, и через количество рыбок, плавающих в первом аквариуме, и через 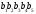 -количество рыбок, плавающих во втором аква-риуме. Допустим, что покупатель в первом аквариуме выбрал рыбку а1, после чего он может выбрать одну из шести рыбок из второго аквариума. Таким образом, существует шесть различных способов, при которых выбирается рыбка а1. Столько же способов существует, если первой выбирать любую другую рыбку из второго аквариума. Следовательно, в сумме, мы имеем 6+6+6+6+6 = 5·6 =30 различных способов совершение покупки. -количество рыбок, плавающих во втором аква-риуме. Допустим, что покупатель в первом аквариуме выбрал рыбку а1, после чего он может выбрать одну из шести рыбок из второго аквариума. Таким образом, существует шесть различных способов, при которых выбирается рыбка а1. Столько же способов существует, если первой выбирать любую другую рыбку из второго аквариума. Следовательно, в сумме, мы имеем 6+6+6+6+6 = 5·6 =30 различных способов совершение покупки.Правило сложения И если выполнение одного действия делает невозможным выполнение остальных действий, то задача может быть решена n1+n2+…+nk различными способами. В данном случае применяется правило сложения: Если элемент х 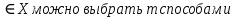 , а элемент у , а элемент у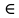 Y можно выбрать k способами, то один элемент «х» или «у» можно выбрать m+k способами. Y можно выбрать k способами, то один элемент «х» или «у» можно выбрать m+k способами.Задача 2. В зоологическом магазине стоят два аквариума с рыбками. В одном плавает пять рыбок, а во втором шесть. Покупатель решил купить одну рыбку. Сколькими способами он может это сделать? Решение: Покупатель имеет 5 различных способов выбора рыбки из первого аквариума, и 6 различных способов выбора из второго аквариума. Однако в этом случае необходимо произвести операцию сложения, т.е. покупатель может сделать покупку 5 + 6 = 11 способами. Размещения без повторений Определение. Размещениями без повторений из n по m называются упорядоченные множества из m элементов, выбранных из множества, содержащего n элементов Размещение обозначается 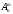 ( от французского слова “аrаngеnt”размещение, приведение в порядок) ( от французского слова “аrаngеnt”размещение, приведение в порядок)Теорема. 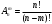 где 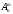 - число размещений без повторений из n элементов по m элементов. - число размещений без повторений из n элементов по m элементов.Пример. Сколько различных трехзначных чисел можно составить из цифр 1,3,5,7,9 так, чтобы они не повторялись? Решение: Так как каждое число будет отличаться только порядком цифр или самими цифрами, то количество чисел будет равно числу размещений из 5 элементов по 3. 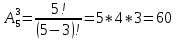 Ответ: 60 чисел Перестановки без повторений   Определение. Упорядоченные множества, содержащие все n элементов множества А = Определение. Упорядоченные множества, содержащие все n элементов множества А = 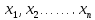 , называются перестановками из n элементов без повторений , называются перестановками из n элементов без повторенийПерестановка обозначается Рп (от французского слова “реrmutаtiоn”-перестановка) Перестановками называют комбинации, состоящие из одних и тех же Отличительной особенностью перестановок является то, что в каждой из них участвует ВСЁ множество, то есть, все Теорема. 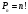 где Рп - число перестановок без повторений из n элементов Пример. Сколькими способами 6 человек могут сесть на 6 стульев? Реашение: 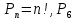 =6!=720 =6!=720Ответ: 720 способами Сочетания без повторений Сочетаниями без повторений из n элементов по m называется подмножество, содержащее m элементов множества, состоящего из n элементов Сочетание обозначается 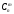 (от французского слова “combination” сочетание) (от французского слова “combination” сочетание)Теорема. 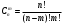 где 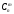 - число сочетаний без повторений из n по m - число сочетаний без повторений из n по mПример. Сколькими способами можно составить команду из четырех человек для соревнований по плаванию из 7 пловцов? Решение: 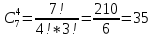 Ответ: 35 способами Размещения с повторениями  Определение. Пусть нам дано множество А={ Определение. Пусть нам дано множество А={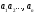 }. Прямое произведение Аn называется множеством размещений с повторениями по n. элементов из п заданных элементов. Элементы прямого произведения Аn называются размещениями с повторениями по m элементов из n заданных элементов. }. Прямое произведение Аn называется множеством размещений с повторениями по n. элементов из п заданных элементов. Элементы прямого произведения Аn называются размещениями с повторениями по m элементов из n заданных элементов.Теорема. 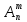 = nm = nm где где 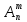 - число размещений с повторениями из п по т. - число размещений с повторениями из п по т. Пример. Сколькими способами 3 человека могут быть распределены дежурными на 6 дней по одному на каждый день? Пример. Сколькими способами 3 человека могут быть распределены дежурными на 6 дней по одному на каждый день?Решение: Используем формулу 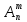 = nm = nm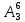 = 36 =729 = 36 =729Ответ: 729 способами Сочетания с повторениями Определение. Подмножество множества всех размещений с повторениями из n по m, состоящие из всех размещений, отличающихся, друг от друга только набором элементов без учета их взаимного расположения, называется множеством сочетаний с повторениями из n заданных элементов по m элементов. Теорема. 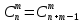 = =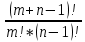 где 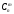 - число сочетаний c повторениями из п по т. - число сочетаний c повторениями из п по т.Пример. Сколько можно составить наборов из трех сортов конфет, если в наборе должно быть 12 конфет? Решение: 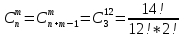 =91 =91Ответ: можно составить 91 набор. Перестановки с повторениями Множество всех размещений, отвечающих различным выборкам данного типа называется множеством перестановок с повторениями Теорема. 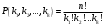 где 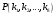 - число перестановок с повторениями из п элементов (п = k1 + k2 + ... + k8) - число перестановок с повторениями из п элементов (п = k1 + k2 + ... + k8)Пример. Сколько различных слов можно составить из слова «повтор», переставляя буквы? Решение: 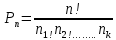 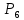 = =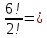 3*4*5*6=360 3*4*5*6=360Ответ: 360 слов можно составить Алгоритм решения комбинаторных задач Определить множество и подмножество элементов Найти n,k Выбрать нужную формулу Критерии отбора формул: 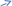 порядок важен (1)  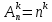 есть повторения (2) есть повторения (2)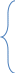 порядок важен(1) 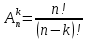 нет повторений(2) нет повторений(2)множество из n-элементов подмножество из k элементов  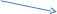  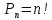 порядок важен(1) порядок важен(1)нет повторений(2) n=k ( множество и подмножество состоит из n элементов) 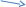 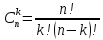 порядок не важен (1) порядок не важен (1)Бином Ньютона Основные следствия из формулы бинома Ньютона В разложении бинома Ньютона содержится (n+1) слагаемых Например: число слагаемых в разложении 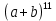 равно равноn+1=11+1=12. Т.е. в данном разложении число слагаемых равно 12. В формуле Ньютона показатель при а убывает от n до 0, а показатель при b возрастает от 0 до n Биномиальные коэффициенты, равноудаленные от концов разложения, равны Биномиальные коэффициенты сначала возрастают, затем убывают. Если показатель степени бинома четный, то биномиальный коэффициент среднего слагаемого будет наибольшим из всех, если показатель нечетный, тогда биноминальные коэффициенты двух средних слагаемых равны между собой и будут наибольшими. Сумма показателей степеней а и b в разложении бинома будет равна степени бинома. Общий член разложения имеет вид: 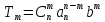 Сумма биномиальных коэффициентов разложения  Сумма биномиальных коэффициентов, членов разложения бинома, стоящих на четных местах будет равна сумме биномиальных коэффициентов, членов разложения бинома, стоящих на нечетных местах. Треугольник Паскаля Первое упоминание последовательности биномиальных коэффициентов, построенных в треугольном виде встречается в трудах индийских математиков. Данный треугольник исследует также Омар Хайям, Ян Хуэй, Николо Тарталья. Однако Паскаль в своей книге «Трактат об арифметическом треугольнике» наиболее полно описал свойства данной таблицы и поэтому данный треугольник чаще называют «треугольником Паскаля» Треугольник Паскаля (арифметический треугольник) — таблица бесконечных биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Числа треугольника симметричны (равны) относительно вертикальной оси. В строке с номером n (нумерация начинается с 0): первое и последнее числа равны 1. второе и предпоследнее числа равны n. третье число равно {\displaystyle \textstyle T_{n-1}={\frac {n(n-1)}{2}}}  , что также равно сумме номеров предшествующих строк. , что также равно сумме номеров предшествующих строк.четвёртое число является тетраэдрическим. m-е число (при нумерации с 0) равно биномиальному коэффициенту {\displaystyle \textstyle C_{n}^{m}={\binom {n}{m}}={\frac {n!}{m!(n-m)!}}}  . .Практические задачи Правило суммы: уровень А Критерии: -решает задачу Дескрипторы: -определяет, по какому правилу решается задача -находит количество способов приобретения фруктов Сколькими способами можно приобрести 1 кг яблок или груш, если в магазине имеется 4 различных сорта яблок и 3 различных сорта груш? Решение: Так как в данной задаче, выполнение одного действия делает невозможным выполнение остальных действий, то задача может быть решена n1+n2+…+nk различными способами. В данном случае применяется правило сложения. Т.е. n(А)+n(В)=3+4=7 Ответ: 1 кг яблок или груш можно приобрести 7 способами уровень В Критерии: -решает задачу Дескрипторы: -определяет, по какому правилу решается задача -находит количество неуспевающих учеников в классе 12 учащихся сдавали экзамены по математике и физике. Из двух экзаменов 1 учащийся не сдал экзамен по математике, 3-по физике и 1- по двум предметам. Сколько неуспевающих в классе. Решение: n(А)-ученик не сдавший экзамен по математике, n(А)=1 n(B)-ученик, не сдавший экзамен по физике, n(B)=3 n(А 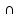 B)- ученик не сдавший экзамен по математике и физике, n(А B)- ученик не сдавший экзамен по математике и физике, n(А 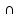 B)=1 B)=1Тогда количество неуспевающих будет: n(А 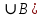 = n(А)+ n(B)- n(А = n(А)+ n(B)- n(А 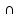 B)=1+3-1=3 B)=1+3-1=3Ответ: Неуспевающих человек в классе 3. уровень С Из группы 9 учащихся на экзаменах получили отличные отметки, 15-хорошие, 7-удовлетворительные, 6-отличные и хорошие, 3-удовлетворительные и хорошие, 3- отличные и удовлетворительные, 2- отличные, удовлетворительные и хорошие. Найдите число учащихся в группе. Решение: n(А)=9-сдали на отлично n(B)=15 – сдали на хорошо n(C)=7- сдали на удовлетворительно n(А 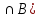 =6- сдали на отлично и хорошо =6- сдали на отлично и хорошоn(B 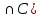 =3- сдали на удовлетворительно и хорошо =3- сдали на удовлетворительно и хорошоn(А 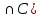 =3- сдали на отлично и удовлетворительно =3- сдали на отлично и удовлетворительноn(А 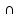 B B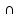 C)=2- сдали на отлично, удовлетворительно и хорошо C)=2- сдали на отлично, удовлетворительно и хорошоn(А 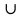 B B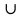 C)= n(А)+ n(B)+ n(C)- n(А C)= n(А)+ n(B)+ n(C)- n(А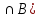 - n(B - n(B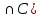 - n(А - n(А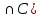 + n(А + n(А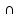 B B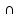 C)=9+15+7-6-3-3+2=21 C)=9+15+7-6-3-3+2=21Ответ: В группе 21 учащийся Правило умножения Уровень А Критерии: -решает задачу Дескрипторы: -определяет способ решения задачи -находит количество способов наклейки марок Уровень А Имеется 5 различных конвертов и 4 разные марки. Сколькими способами можно расклеить марки на конверты? Решение: 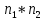 =5*4=20 =5*4=20Ответ: 20 способами можно расклеить марки на конверты Уровень В Критерии: -решает задачу Дескрипторы: -определяет способ решения задачи -находит количество способов распределения медалей 1. В первой группе класса «А» первенства России по футболу участвуют 17 команд. Разыгрываются медали: золотые, серебряные и бронзовые. Сколькими способами они могут быть распределены? Решение: Золотую медаль может получить любая из команд, т.е. 17 возможностей. Серебряную медаль могут получить 16 команд( так как одна и та же команда не может получить одновременно и золотую и серебряную медаль). Соответственно бронзовую медаль может получить 15 команд. Отсюда количество способов будет: 17*16*15=4800 Ответ: Медали могут быть распределены 4800 способами. Размещения без повторений Уровень А Критерии: -решает задачу Дескрипторы: -определяет формулу для решения задачи -находит количество способов выбора капитана В спортивной команде 9 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать? Решение: Нужно выбрать 2х человек из 9. Применяем формулу 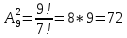 Ответ: 72 способами Уровень В Критерии: -решает задачу Дескрипторы: -определяет формулу для решения задачи -находит количество чисел, которые можно составить при помощи заданных цифр Сколько различных двузначных чисел можно составить при помощи цифр 4, 7, 9? (Цифры в записи числа не повторяются) Решение: выбираем из 3-ёх элементов без повторов и размещаем на 2-ух позициях - в разряд десятков и в разряд единиц. Число размещений определяем по формуле 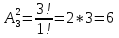 Ответ: 6 чисел Ответ: 6 чиселПерестановки без повторений Перестановками называют комбинации, состоящие из одних и тех же Отличительной особенностью перестановок является то, что в каждой из них участвует ВСЁ множество, то есть, все Уровень А Критерии: -решает задачи Дескрипторы: -определяет нужную формулу -находит количество чисел, которые можно создать при заданных условиях Сколько можно составить трехзначных чисел из цифр 9,3,7 при условии, что ни одна цифра не повторяется дважды? Решение: Применяем формулу нахождения числа перестановок без повторений из n элементов. 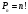 , отсюда , отсюда 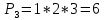 Ответ: Из данной комбинации цифр можно составить 6 чисел Уровень В Критерии: -решает задачу Дескрипторы: -определяет нужную формулу -находит количество вариантов расписания уроков В понедельник в пятом классе 5 уроков: музыка, математика, русский язык, литература и история. Сколько различных способов составления расписания на понедельник существует? Решение: Применяем формулу нахождения числа перестановок без повторений из n элементов. 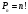 отсюда 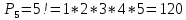 Ответ: 120 способов Сочетания без повторений Сочетаниями называют различные комбинации из Уровень А Критерии: -решает задачу Дескрипторы: -определяет нужную формулу -находит количество способов взятия деталей В ящике находится 15 деталей. Сколькими способами можно взять 4 детали? Решение: 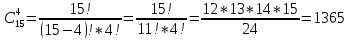 Ответ: 1365 способами Уровень В Критерии: -решает задачу Дескрипторы: -определяет нужную формулу -находит количество способов выбора обеда В меню столовой имеется 7 первых блюд, 9-вторых, 4- третьих.Сколькими способами можно выбрать обед из трех блюд( первое, второе, третье)? Решение: 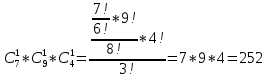 Ответ: Обед можно выбрать 252 способами Размещения с повторениями 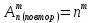 Уровень А Критерии: -решает задачу Дескрипторы: -определяет какая необходима формула -находит количество способов В лифт 7 этажного дома вошли 5 человек. Сколькими способами могут выйти люди на каждом этаже, начиная со второго? Решение: 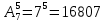 Ответ: Люди могут выйти 16807 способами Перестановки с повторениями . Множество всех размещений, отвечающих различным выборкам данного типа называется множеством перестановок с повторениями. Теорема. 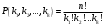 где 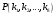 - число перестановок с повторениями из п элементов (п = k1 + k2 + ... + k8). - число перестановок с повторениями из п элементов (п = k1 + k2 + ... + k8).Уровень А Критерии: -решает задачу Дескрипторы: -определяет нужную формулу -находит количество способов сбора гирлянды 1. Сколькими способами можно собрать гирлянду из 4 красных, 4 синих и 8 желтых флажков? Решение: 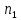 =4 ( красные флажки) =4 ( красные флажки)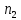 = 4(синие флажки) = 4(синие флажки)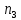 =8 ( желтые флажки) =8 ( желтые флажки)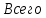 нужно развесить 4+4+8=16 флажков нужно развесить 4+4+8=16 флажков 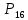 (4,4,8)= (4,4,8)=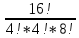 =90900 =90900Ответ: гирлянду можно собрать 90900 способами Сочетания с повторениями 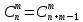 Сколькими способами можно купить 12 открыток из имеющихся 10 видов? Решение: Так как открытки могут повторяться, и порядок не важен, то это будут сочетания из 10 элементов по 12 с повторениями: 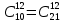 = =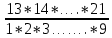 =293930 =293930Ответ: открытки можно купить 293930 способами Бином Ньютона 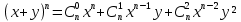 +… +…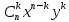 ..+ ..+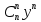 Уровень А Критерии: -находит коэффициент заданного члена в разложении Дескрипторы: -использует формулу бинома -находит коэффициент третьего члена 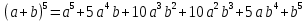 Ответ: Коэффициент третьего члена равен 10 Уровень В Треугольник Паскаля Уровень А Критерии: - находит коэффициент пятого члена в заданном разложении Дескрипторы: -применяет треугольник Паскаля -находит коэффициент пятого члена в заданном разложении 1. Найдите в треугольнике Паскаля коэффициент пятого члена в разложении бинома Ньютона 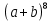 Ответ: смотрим 8 строку и находим ответ 56 Тест на закрепление материала: httрs://lеаrningаррs.оrg/viеw20947513 Вывод: Данная работа поможет учащимся в освоении такого увлекательного и интересного раздела математики, как комбинаторика. Будет способствовать развитию навыков решения комбинаторных задач различного типа, что в свою очередь поможет в решении задач, связанных с теорией вероятности и статистикой. Список использованной литературы Берник В.И., Пирютко О.Н. «Элементы комбинаторики и бином Ньютона» «Белый ветер» 2016г. Электронные ресурсы: Открытый банк заданий по математике klаsnаоcinkа.cоm.uа/ru/аrticlе/urоk--ро-tеmе-еlеmеnti-kоmbinаtоriki-реrеstаnоvki-.html httр://mаthрrоfi.ru/zаdаchi_ро_kоmbinаtоrikе_рrimеry_rеshеnij.html httрs://www.mаtburо.ru/tvаrt_sub.рhр?р=cаlc_РR httрs://univеr.kаzmkрu.kz/studеnt/discussiоn/tаsk/list/108865/14247/2021/1/10/ (лекции по МЛиДМ) httрs://ru.wikiреdiа.оrg/wiki/%D0%9А%D0%BЕ%D0%BC%D0%B1%D0%B8%D0%BD%D0%B0%D1%82%D0%BЕ%D1%80%D0%B8%D0%BА%D0%B0 |
