КР. 12 учеников класса имеют отличные оценки, 16 удовлетворительные, 5 и отличные и удовлетворительные. Сколько учеников в классе
 Скачать 269.69 Kb. Скачать 269.69 Kb.
|
|
Вариант 4 Задание 1 A = {1, 2, 3, 4, 5, 6, 7, 8}; B = {3, 4, 5, 6, 9, 10, 11, 12}; C = {5, 6, 7, 8, 9, 10, 13, 14}. D1 = A \ B = 1,2,7,8 D2 = B Ç С = 5,6,9,10 D = D1 x D2 = (1,5), (1,6) , (1,9) , (1,10), (2,5), (2,6) , (2,9) , (2,10), (7,5), (7,6) , (7,9) , (7,10), (8,5), (8,6) , (8,9) , (8,10) Задание 2 12 учеников класса имеют отличные оценки, 16 – удовлетворительные, 5 – и отличные и удовлетворительные. Сколько учеников в классе? 12+(16-5) = 23 Задание 3 Построить таблицу истинности для следующих выражений и представить их в СДНФ и СКНФ, минимизировать, используя метод Карт Карно, построить полином Жегалкина.
СДНФ ¬P¬Q¬R ∨ ¬P¬QR ∨ ¬PQ¬R ∨ ¬PQR ∨ P¬Q¬R ∨ PQ¬R ∨ PQR СКНФ ¬P∨Q∨¬R Карта Карно
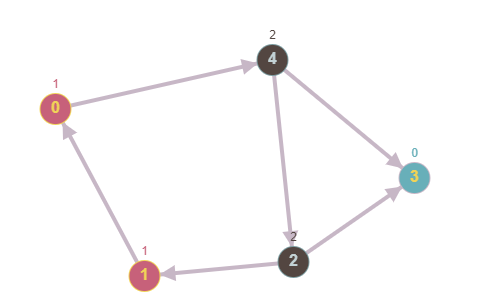
Полином Жегалкина 1⊕PR⊕PQR Задание 4 По матрице смежности восстановите ориентированный граф D, взяв в качестве вершин V1, V2, V3, V4, V5 пять произвольных точек плоскости. Найдите: 1) матрицу инцидентности B, предварительно перенумеровав ребра; 2) степени вершин графа; Изобразите граф 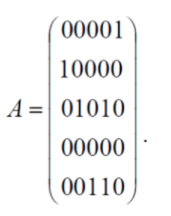 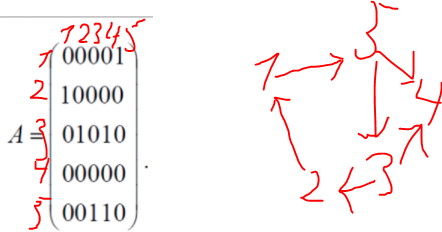
 Задание 5. Дан ориентированный граф D. 1.Решите задачу о наибольшем потоке в транспортной сети 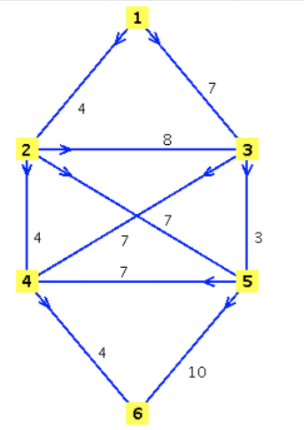 1=1-3-4-6 min 4 2=1-2-5-6 min 4 3=1-3-5-6 min 3 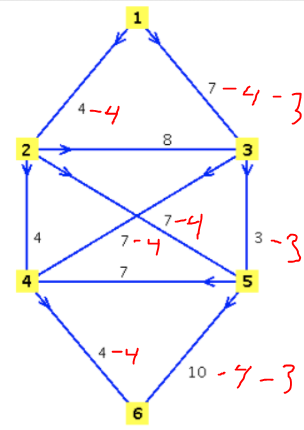 Задание 6. Найдите минимальное остовное дерево в неориентированном нагруженном графе методом Прима 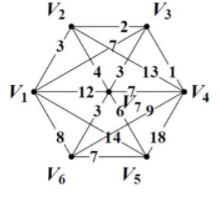 - -
1-2 2-3 3-4 3-7 7-6 7-5 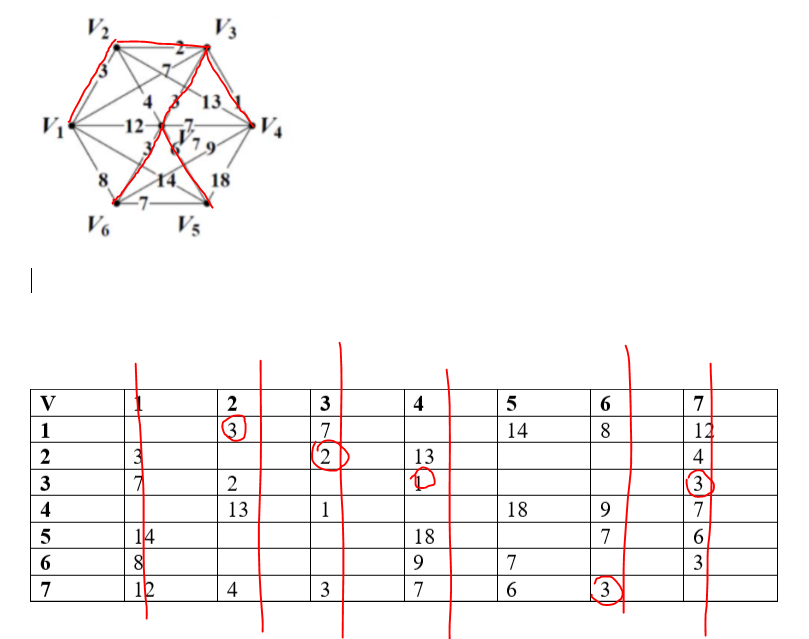 3+2+1+6+3+3=18 |
