1. Ядерная реакция
 Скачать 1.48 Mb. Скачать 1.48 Mb.
|
|
1.Ядерная реакция – это процесс превращения одних ядер в другие при их столкновении друг с другом или с какими-либо частицами. Радиоактивный распад нестабильных ядер также является разновидностью ядерных реакций. Рассмотрим случай столкновения двух ядер, в результате которого получаются два новых ядра. Вместо некоторых ядер могут быть частицы: нейтрон, электрон, γ квант и др. 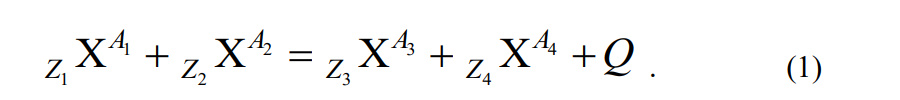 Нижние индексы обозначают заряды частиц, верхние – число нуклонов в ядре: если частица не содержит нуклонов и не является сама нуклоном, то A=0. X – символ элемента или частицы. В левой части обозначены сталкивающиеся частицы, в правой – продукты реакции. Q – энергия, выделившаяся при реакции. При ядерных реакциях выполняются законы сохранения импульса, полной энергии, электрического заряда и числа нуклонов. Последние два закона позволяют определить тип одной из частиц, если известны остальные. Запишем эти законы. 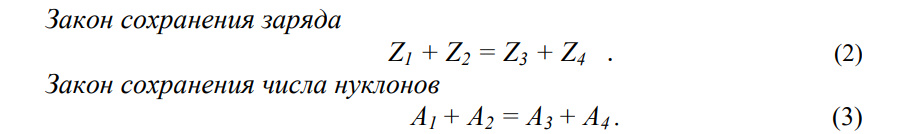 2.Постулаты Бора. Первая попытка построить качественно новую – квантовую – теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором (1885-1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовые характеристики излучения и поглощения света. В основу теории Бор положил три постулата. I постулат Бора: в атомах существуют стационарные (не изменяющиеся со временем) состояния, в которых атом не излучает энергию. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн. II постулат Бора: в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные значения момента импульса, удовлетворяющие условию: III постулат Бора: при переходе атома из одного стационарного состояния в другое излучается или поглощается один фотон энергией, равной разности энергий стационарных состояний  3.Естественный и поляризованный свет. Виды поляризации. 1) Свет, в котором все направления колебаний светового вектора в плоскости, перпендикулярной направлению распространения волны, равновероятны, называется естественным или неполяризованным 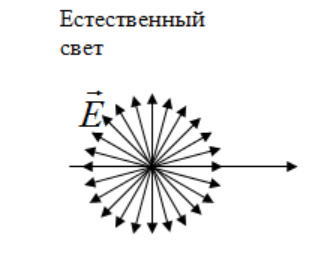 Поляризованным называется свет, в котором направления колебания вектора E упорядочены каким-либо образом. 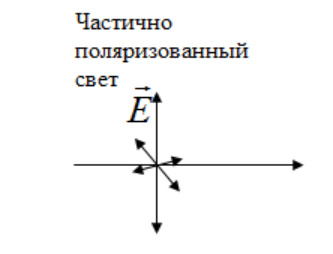 2) Свет, в котором вектор Е колеблется только в одном направлении, называется плоско (линейно) поляризованным светом (электромагнитной волной). 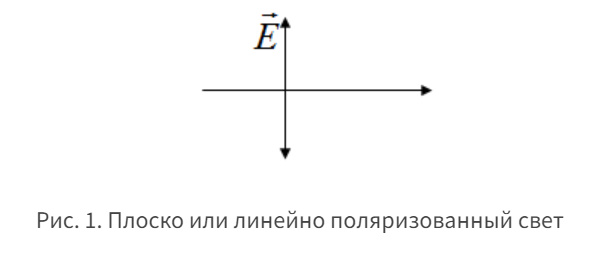 В плоско поляризованном свете плоскость, в которой колеблется вектор Е, называется плоскостью поляризации, плоскость, в которой колеблется вектор H называется плоскостью колебаний. Различают также эллиптически поляризованный свет: при распространении электрически поляризованного света вектор E описывает эллипс, и в частном случае, циркулярно поляризованный свет или свет круговой поляризации, в котором вектор E описывает окружность (сравните со сложением взаимно перпендикулярных колебаний: возможны: прямая линия, эллипс и окружность). 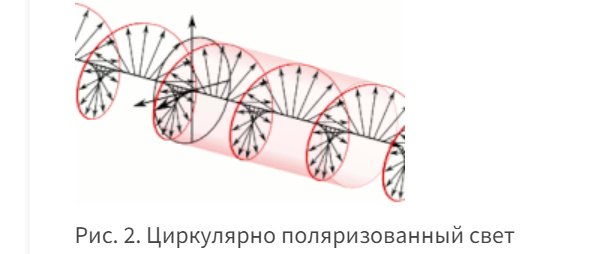 3) Естественный свет можно преобразовать в плоско поляризованный, используя поляризатор - устройство, пропускающее колебания только определенного направления, параллельные главной плоскости поляризатора, и полностью задерживающие колебания, перпендикулярные этой плоскости. 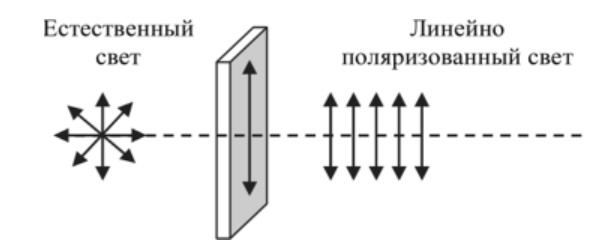 В качестве поляризаторов могут быть использованы среды, анизотропные в отношении колебаний вектора , например кристаллы. Из природных кристаллов, используемых в качестве поляризатора, следует отметить турмалин. Анализатор – устройство, которое позволяет определять, поляризован свет или нет, и регулировать его интенсивность. 4) Закон Малюса: если на поляризатор (или анализатор) падает поляризованный свет, то интенсивность света I, прошедшего через поляризатор (или анализатор), пропорциональна квадрату косинуса угла ψ между главной плоскостью поляризатора и направлением плоскости поляризации, т. е. 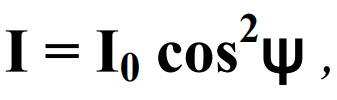 где I0 - интенсивность поляризованного света, падающего на анализатор. Если на поляризатор (или анализатор) падает неполяризованный свет, то через него пройдет ровно половина интенсивности падающего света. 17. Способы получения поляризованного света. Закон Брюстера. Двойное лучепреломление. 1) (это не из мудла) Способы получения поляризованного света: 1. Поляризация при отражении и преломлении. Если естественный свет падает на отражающую поверхность диэлектрика (стекла, слюды и т. п.) под углом а, удовлетворяющим условию Брюстера: 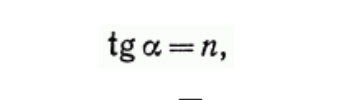 то отраженная волна оказывается плоскополяризованной 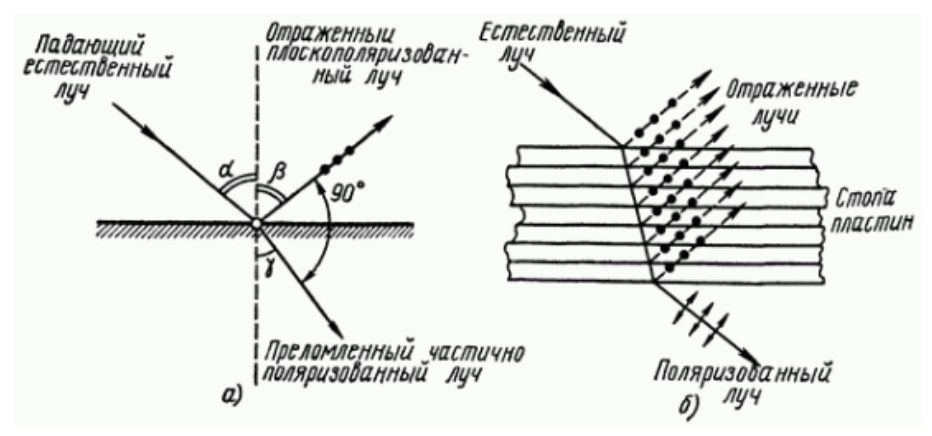 2. Поляризация при двойном лучепреломлении в кристаллах; призма Николя. При преломлении света на границе оптически анизотропных сред, например кристаллов, естественный луч расщепляется на два луча (обыкновенный и необыкновенный), поляризованные в двух взаимно перпендикулярных плоскостях. 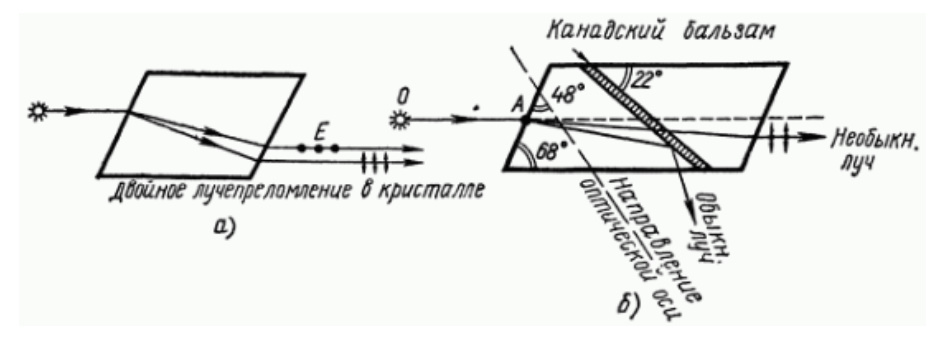 3. Поляризация при прохождении света через поглощающие анизотропные вещества; поляроиды. 2) Закон Брюстера - луч, отраженный от границы раздела двух диэлектриков, полностью поляризован, если угол падения αБ удовлетворяет условию: 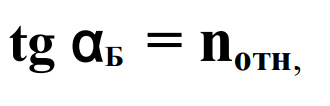 где nотн - относительный показатель преломления. Для угла Брюстера ρ||=0. 3) Поляроиды- прозрачные пленки (полимерные, монокристаллические и др.), преобразующие неполяризованный свет в линейно поляризованный, т.к. пропускают свет только одного направления поляризации. Квантовые числа Каждому набору квантовых чисел соответствует определенное значение волновой функции и энергии электрона. Всего квантовых чисел 4: n – главное, l - орбитальное, ml - магнитное, ms - спиновое. 1)Главное квантовое число n – определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения (n=1,2,3...). 2)Орбитальное квантовое число l– определяет момент импульса электрона в атоме, при заданном значении принимает значения l=0,1,2,…n-1 то есть всего n значений. 3)Магнитное квантовое числоml – определяет проекцию момента импульса электрона на заданное направление, причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентаций. 4) нет даже в лекциях Квантовые числа и их значения являются следствием решений уравнения Шредингера и условий однозначности, непрерывности и конечности налагаемых на волновую функцию. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве. 4.Интерференция света. Интерференция света – это явление наложения когерентных световых волн, в результате которого происходит перераспределение энергии светового поля, т.е. образуются светлые участки (максимумы) и тёмные участки (минимумы) интерференционной картины. Интерференционная картина – регулярное чередование областей повышенной и пониженной интенсивности света, получающееся в результате наложения когерентных световых пучков, т. е. в условиях постоянной (или регулярно меняющейся) разности фаз между ними. __________________________________________________________________________________________________ 6.Условия максимума и минимума интерференционной картины. Когерентные волны. Условие max: оптическая разность хода двух волн равна чётному числу полуволн: Δ=2k 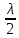 , k=0, ±1, ±2, ... . , k=0, ±1, ±2, ... .Условие min: оптическая разность хода двух волн равна нечётному числу полуволн Δ=(2k+1) 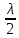 , k=0, ±1, ±2, ... . , k=0, ±1, ±2, ... .Когерентные волны – волны, разность фаз которых в данной точке пространства остается постоянной во времени. Когерентными могут быть только волны, имеющие одинаковую частоту (длину волны), т.е. волны монохроматические (например, свет от обычных источников является некогерентным). __________________________________________________________________________________________________ 7. Способы получения когерентных волн в оптике. Опыт Юнга. Р 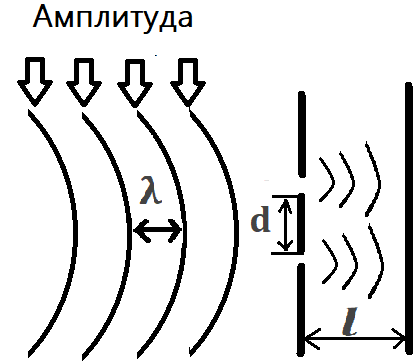 асстояние между двумя соседними максимумами или минимумами: асстояние между двумя соседними максимумами или минимумами: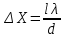 (не зависит от порядка интерференции k) (не зависит от порядка интерференции k) Когерентные волны, приходящие от щелей, Усилят друг друга при условии Отверстия малы и находятся близко друг к другу – это щели. При 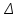 = k = k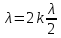 попадании волны происходит дифракция. Когда волны (k=0,±1,±2,...) пересекаются, они усиливают друг друга (появляется светлое пятно) попадании волны происходит дифракция. Когда волны (k=0,±1,±2,...) пересекаются, они усиливают друг друга (появляется светлое пятно) . . __________________________________________________________________________________________________ 8. Интерференция в тонких пленках. Полосы равного наклона. Интерференционная картина в плоскопараллельных пластинах (плёнках) определяется величинами λ, h, n и α. Для данных λ, h, n каждому наклону α лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Лучи 1′ и 1″, отразившиеся от верхней и нижней граней пластинки, параллельны друг другу, так как пластинка плоскопараллельна. 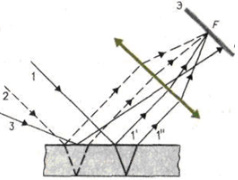 Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. _________________________________________________________________________________________________ 9. Интерференция в тонких пленках. Полосы равной толщины. Для достаточно тонкой пластинки или плёнки можно наблюдать интерференционную картину, локализованную вблизи отражающей поверхности. Получающиеся в результате интерференционные полосы называют полосами равной толщины. В белом свете интерференционные полосы окрашены. Такое явление называют цветами тонких плёнок (пример: мыльные пузыри). __________________________________________________________________________________________________ 10. Кольца Ньютона. Н  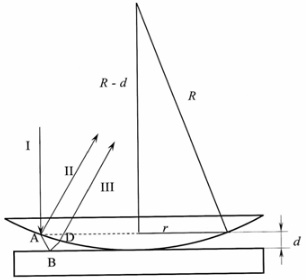 аблюдаются в том случае, когда выпуклая поверхность линзы малой кривизны соприкасается с плоской поверхностью хорошо отполированной пластинки, так что остающаяся между ними воздушная прослойка постепенно утолщается от центра к краям аблюдаются в том случае, когда выпуклая поверхность линзы малой кривизны соприкасается с плоской поверхностью хорошо отполированной пластинки, так что остающаяся между ними воздушная прослойка постепенно утолщается от центра к краямЕсли на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней границ этой воздушной прослойки, будут интерферировать между собой. Получится тёмное пятно в центре, округлённое светлыми и тёмными кольцами убывающей ширины. Общий центр колец расположен в точке касания. В отраженном свете центр темный, так как при толщине воздушной прослойки, намного меньшей, чем длина волныλ,разность фаз интерферирующих волн обусловлена различием в условиях отражения на двух поверхностях. Радиус темного кольца с номером k Выражение для радиуса k-го светлого кольца с учетом максимума интерференции Δ=kλ имеет вид: Если линзу постепенно отодвигать от поверхности стекла, то интерференционные кольца будут стягиваться к центру. При увеличении расстояния на 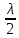 картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света. картина принимает прежний вид, так как место каждого кольца будет занято кольцом следующего порядка. С помощью колец Ньютона, как и в опыте Юнга, можно сравнительно простыми средствами приближенно определить длину волны света.________________________________________________________________________________________________ 11. Применение интерференции. Интерферометры. Явление интерференции применяется в интерферометрах. Интерферометр – оптический измерительный прибор, основанный на интерференции света. Он позволяет с высокой степенью точности измерять линейные и угловые расстояния, малые разности показателей преломления, исследовать структуру спектральных линий и т.п. Первый его сделал Альберт Майкельсон. М 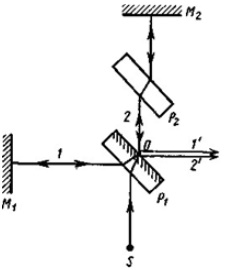 онохроматический свет от источника S падает под углом 45° на плоскопараллельную пластинку P1, задняя сторона которой покрыта тонким полупрозрачным слоем серебра. Здесь пучок разделяется на два взаимно перпендикулярных пучка. Отраженный пластинкой P1, пучок падает на зеркало M1, отражается назад, вновь попадает на пластинку P1, где снова разделяется на две части. Одна из них идет к источнику S и не представляет интереса, а другая попадает в зрительную трубу, настроенную на бесконечность, или на линзу, в фокальной плоскости которой расположен экран для наблюдения интерференции. онохроматический свет от источника S падает под углом 45° на плоскопараллельную пластинку P1, задняя сторона которой покрыта тонким полупрозрачным слоем серебра. Здесь пучок разделяется на два взаимно перпендикулярных пучка. Отраженный пластинкой P1, пучок падает на зеркало M1, отражается назад, вновь попадает на пластинку P1, где снова разделяется на две части. Одна из них идет к источнику S и не представляет интереса, а другая попадает в зрительную трубу, настроенную на бесконечность, или на линзу, в фокальной плоскости которой расположен экран для наблюдения интерференции.Прошедший сквозь пластинку P1 пучок от источника падает на зеркало M2, возвращается к P1 и частично отражается в сторону линзы. Таким образом, от одного источника S получаются два пучка примерно одинаковой интенсивности, которые распространяются после разделения пластинкой P1 в разных «плечах» интерферометра, затем снова встречаются и создают интерференционную картину в фокальной плоскости линзы. Пластинка P2, такая же, как и P1, только без отражающего покрытия, ставится на пути второго пучка для компенсации разности хода, возникающей из-за того, что первый пучок проходит через P1 три раза, а второй - только один раз. Зеркало M2 неподвижно, а зеркало M1 можно передвигать микрометрическим винтом так, что его плоскость все время остается перпендикулярной зеркалу M2. При перемещении зеркала M1 на расстояние 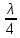 разность хода обоих лучей изменяется на разность хода обоих лучей изменяется на 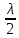 и происходит смена освещенности экрана. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении зеркала M1 и использовать интерферометр Майкельсона для точного (порядка 10−7 м) измерения длин. и происходит смена освещенности экрана. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении зеркала M1 и использовать интерферометр Майкельсона для точного (порядка 10−7 м) измерения длин.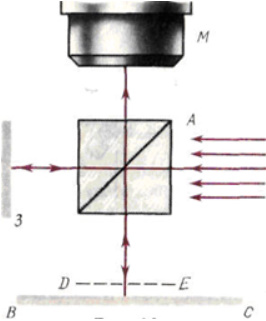 Микроинтерферометр – комбинация интерферометра и микроскопа (создал его В.П. Линник). Основным элементом микроинтерферометра Линника является стеклянный куб А, состоящий из двух половин, склеенных до диагональной плоскости. Одна из стеклянных поверхностей полупосеребрена. Ход лучей интерферометра показан на рисунке, где ВС – исследуемая плоская поверхность, а З – плоское зеркало. Двугранный угол между зеркалом и поверхностью ВС отличается от π/2на малую величину α. Штриховая линия DE – мнимое изображение отражающей поверхности зеркала З в полупосеребренной диагональной поверхности куба А. Интерференционные полосы равной толщины для воздушного клина DE–BC наблюдаются с помощью микроскопа М. В тех местах поверхности ВС, где имеются выступы или углубления, наблюдаются искривления интерференционных полос. С помощью этого прибора можно обнаружить штрихи на поверхности детали, глубина которых порядка 10−7 м. 1 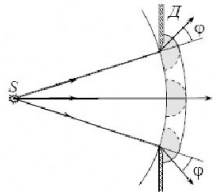 2. Дифракция света. Принцип Гюйгенса-Френеля. 2. Дифракция света. Принцип Гюйгенса-Френеля.Дифракцией называется огибание волнами препятствий, встречающихся на их пути. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т.д. Я 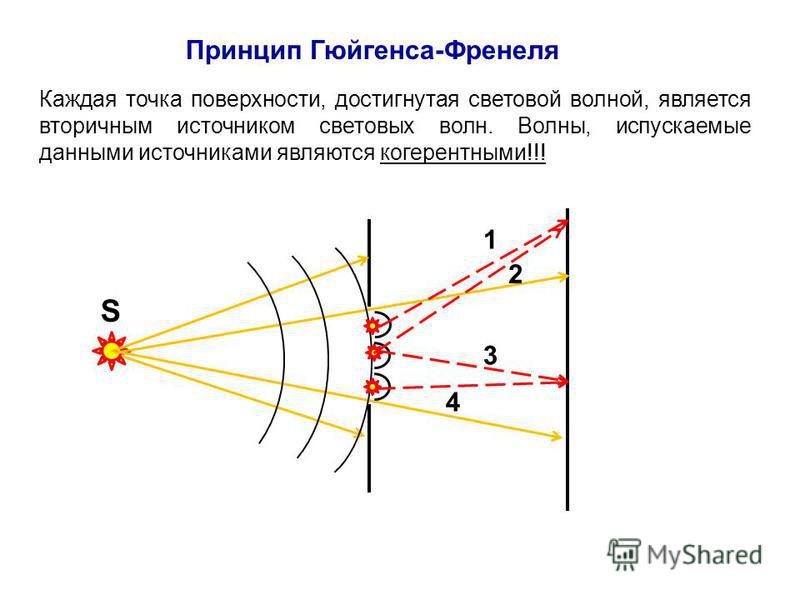 вление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т.е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его. (это чтобы было понятнее) вление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т.е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его. (это чтобы было понятнее)Принцип Гюйгенса-Френеля: Световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, "излучаемых" фиктивными источниками. __________________________________________________________________________________________________ 1 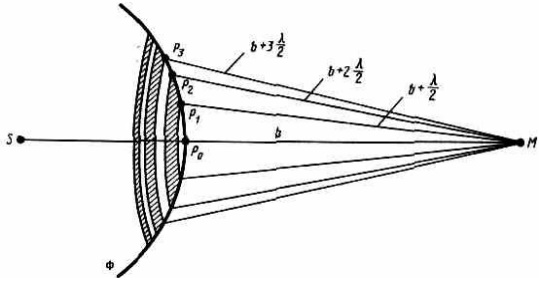 3. Зоны Френеля, объяснение на их основе явления дифракции. Зонные пластинки. 3. Зоны Френеля, объяснение на их основе явления дифракции. Зонные пластинки. Сам метод Зон Френеля надо рассказать. Дифракция – интерференция бесконечного количества источников. Принцип Гюйгенса-Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространение света. Френель решил эту задачу, рассмотрев взаимную интерференцию вторичных волн и применив прием, получивший название метод зон Френеля: волновая поверхность разбивается на кольцевые зоны – зоны Френеля. Расстояние от крайних точек соседних зон до точки наблюдения отличается на 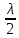 Зонная пластинка - плоскопараллельная стеклянная пластинка с выгравированными концентрическими окружностями, радиус которых совпадает с радиусами зон Френеля. З  онная пластинка «выключает» четные либо нечетные зоны Френеля, чем исключает взаимную интерференцию (гашение) от соседних зон, что приводит к увеличению освещенности точки наблюдения. Таким образом зонная пластинка действует как собирающая линза. онная пластинка «выключает» четные либо нечетные зоны Френеля, чем исключает взаимную интерференцию (гашение) от соседних зон, что приводит к увеличению освещенности точки наблюдения. Таким образом зонная пластинка действует как собирающая линза.__________________________________________________________________________________________________ 14. Дифракционная решетка: устройство и принцип действия. Дифракционная решетка – система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Д 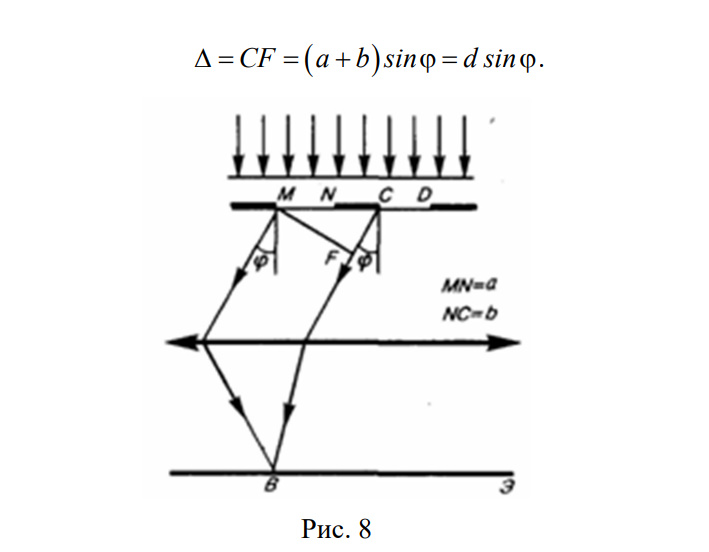 ифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. ифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.Рассмотрим дифракционную решетку (рис. 8). Если ширина каждой щелей ровна a, а ширина непрозрачного участка между щелями b, то величина d=a + b называется постоянной (периодом) дифракционной решетки. Разность хода двух соседних лучей в пределах решетки будет везде одинакова и равна: Атом Бора. 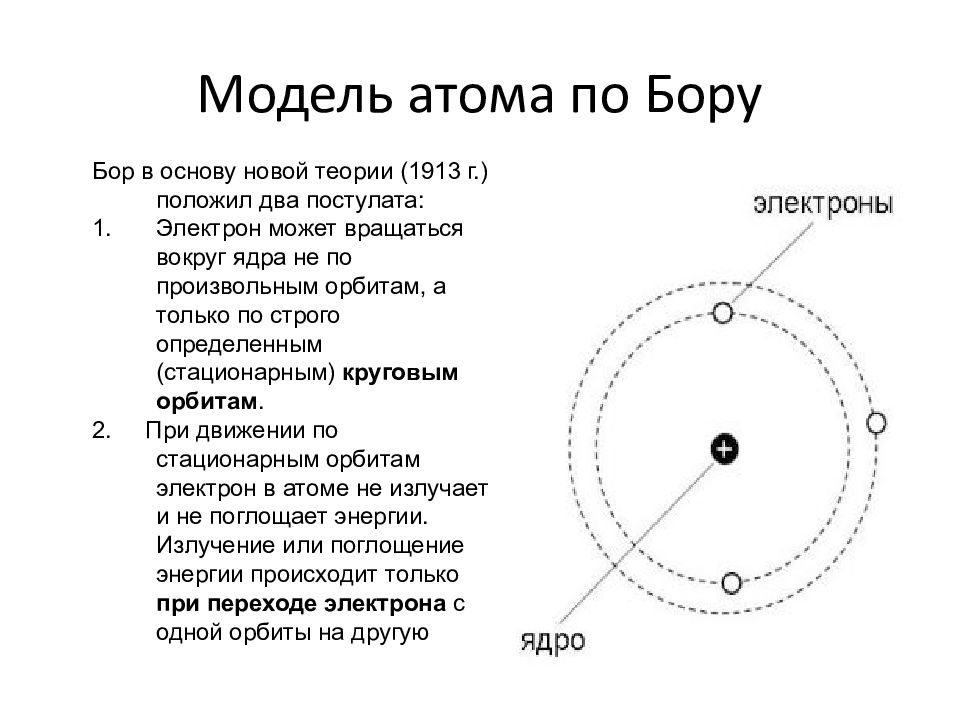 Спектральные серии атома водорода. Спектральные серии. К одной серии относят линии с одним значением k и разными значениями n>k. 1-я серия, серия Лаймана: k=1, n=2,3,4,…. . Лежит в ультрафиолетовой области спектра. 2-я серия, серия Бальмера: k=2, n=3,4,5,…. . Лежит в видимой области спектра. 3-я серия, серия Пашена: k=3, n=4,5,6, …. . Лежит в инфракрасной области спектра. 24. Атомное ядро и его характеристики. Изотопы. Т  ут всё важно ут всё важно25. Дефект массы и энергия связи атомного ядра. Дефект массы — разность между суммой масс покоя нуклонов, составляющих ядро, и массойпокоя атомного ядра. Дефект массы характеризует устойчивость ядра. Обозначается Δm: 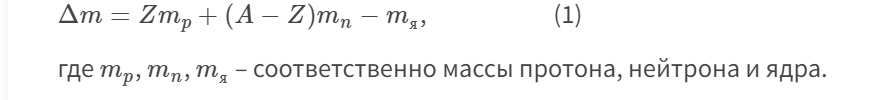 Однако в таблицах масс приводятся, как правило, не массы ядер, а массы нейтральных атомов, в этом случае необходимо применять формулу: 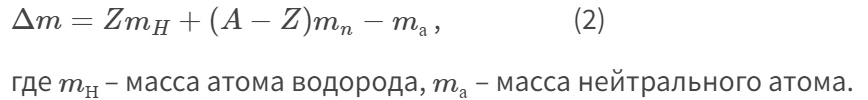 Для разделения ядра на составные части необходимо затратить такое же количество энергии, которое выделяется при его образовании. Энергия, которую необходимо затратить, чтобы расщепить ядро на отдельные нуклоны, называется энергией связи ядра. Согласно соотношению Эйнштейна, энергия связи пропорциональна дефекту массы 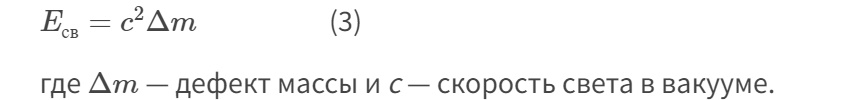 Дефект массы принято выражать в атомных единицах массы (а.е.м.), а энергию связи ядра в мега электрон-вольтах (МэВ). Если перевести атомные единицы массы (а.е.м.) в килограммы (кг), а джоули (Дж) в мега электрон-вольты (МэВ), то получим, что 1 а.е.м. соответствует 931 МэВ, т.е. можно применять формулу для энергии связи в виде: Теория атома по Бору Запишем систему двух уравнений при вращении электрона по круговой орбите вокруг ядра с центростремительным ускорением: - условие квантования момента импульса электрона; - второй закон Ньютона: ma = F 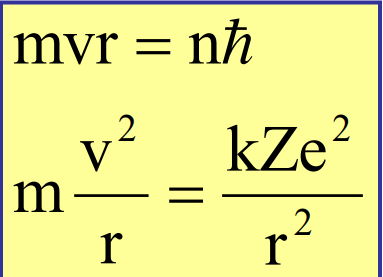 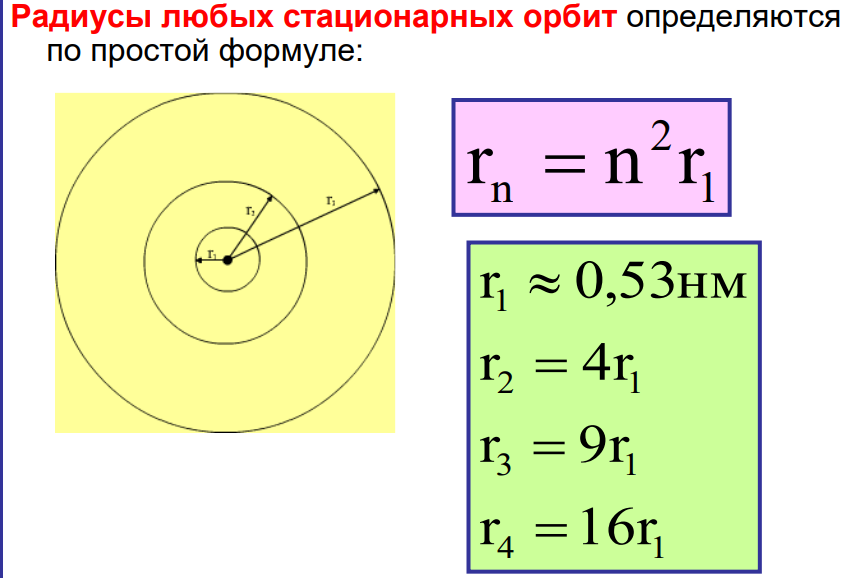 Получим полную энергию электрона: 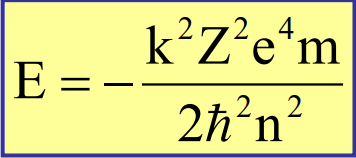 Атомная модель по Шрёдингеру Атомная модель по Шрёдингеру называют также квантово-механической моделью атома. Теперь электрон описывался не как частица, как мы это привыкли видеть ранее и воспринимать (ибо так проще и понятнее), которая похожа на теннисный мячик, а как волна. По представлениям Шрёдингера, вокруг ядра атома существует электронное облако, где электроны могут быть описаны как стоячая волна с вероятностным её расположением. Итак, чему учил Шредингер: Электроны ведут себя как стоячие волны, а их распределение в пространстве описывается волновой функцией Никаких орбиталей у электронов нет, зато есть зоны, где веротянее всего электрон появится. Ну а посчитать это можно через волновую функцию.  Фотоэффект Фотоэффе́кт, или фотоэлектри́ческий эффе́кт, — явление взаимодействия света или любого другого электромагнитного излучения с веществом, при котором энергия фотонов передаётся электронам вещества. В конденсированных (твёрдых и жидких) веществах выделяют внешний (поглощение фотонов сопровождается вылетом электронов за пределы вещества) и внутренний (электроны, оставаясь в веществе, изменяют в нём своё энергетическое состояние) фотоэффект. Фотоэффект в газах состоит в ионизации атомов или молекул под действием излучения.  Волновая оптика Волновая оптика – раздел оптики, объясняющий оптические явления на основе волновой природы света. Световые волны рассматриваются по своей природе как электромагнитные волны, обладающие всеми их свойствами. Волновая оптика описывает такие оптические явления, как интерференция, дифракция, поляризация и дисперсия. Дисперсия является следствием различной скорости распространения волн разной частоты в одной и той же среде. Чем больше частота световой волны, тем меньше ее длина и скорость в среде, тем больше для нее показатель преломления.  Дифракция света Согласно геометрической оптике на экране в результате прохождения световых лучей через отверстие диаметром d появляется изображение в виде яркого круглого пятна большего диаметра D (рис. 131). 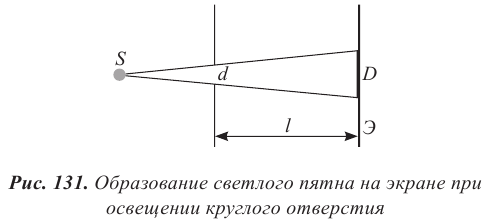 Поляризация волн Колебания зарядов в передающей антенне происходит вдоль антенны, поэтому в электромагнитной волне вектор напряженности расположен в той же плоскости, что и антенна. Вынужденные электрические колебания в приемной антенне совершаются свободными электронами под действием электрического поля волны. Это свидетельствует как о поперечности электромагнитной волны, так и о ее поляризации. Плоскость, проходящую через вектор напряженности электромагнитной волны, и направление ее распространения, называют плоскостью поляризации 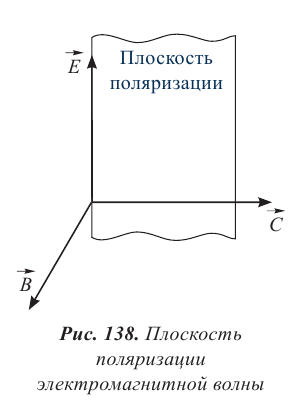 Интерференция Как известно, если направить пучок на любую поверхность, то ее освещенность увеличится. Иную картину можно наблюдать, когда на поверхность надают дна пучка света от одного источника, накладываясь один на другой (рис. 4.15). В случае попадания их на один и тот же участок поверхности наблюдается чередование максимумов и минимумов освещенности. Такую картину от двух щелей впервые наблюдал в 1801 г. английский ученый Т. Юнг, давший впоследствии объяснение данному явлению на основании волновой теории света. |
