Логистика, 2 курс. Контрольная. 1. Закупочная логистика. Планирование и методы закупок
 Скачать 0.56 Mb.
|
Задача 2. Оптимизация маятникого маршрута с обратным холостым пробегомРассчитать оптимальный план работы автомобиля на маятниковом маршруте с обратным холостым пробегом, а также коэффициент использования пробега по данным, представленным в таблице 1. Построить график работы автомобиля на маршруте. Таблица 1 Исходные данные
Решение: Рассчитаем по формуле (11) количество ездок, которые должен сделать автомобиль для перевоза груза в пункты Б1 и Б2
где n - количество ездок, шт.; Q - объем перевозки, т.; q - грузоподъемность автомобиля, т.;
Рассчитаем количество ездок в пункты Б1 и Б2: 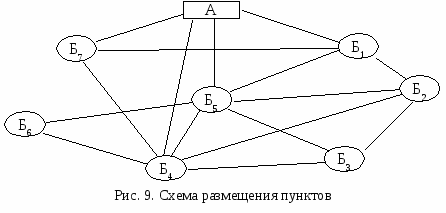    Таким образом автомобиль должен сделать две ездки в пункт Б1, одну ездку в пункт Б2 и одну в Б3 Для решения задачи заполняются таблицы 2-7: Таблица 2 Исходные данные
Таблица 3 Расстояния, км
Таблица 4 Затраты времени на движение автомобиля между пунктами, мин.
Таблица 5 Затраты времени на одну ездку, мин.
Таблица 6 Правила заполнения рабочей матрицы
Таблица 7 Рабочая матрица
Пункт с минимальной разностью расстояний принимается за конечный пункт, т. е. из этого пункта автомобиль едет в гараж, а пункт с максимальной разностью расстояний принимается за начальный. Значит пункт Б3 – начальный, а Б1 - конечный. Г 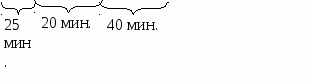 – А – Б3 – А – Б2 – А – Б1 – А – Б1 – Г (105 + 15) = 25 + 20 +40 +105 +15 = 205 мин.Время, затрачиваемое на движение автомобиля – 205 мин. Оптимальный план работы автомобиля на маятниковом маршруте с обратным холостым пробегом составлен. Время, затрачиваемое на маршрут: 205 мин. Т. е. автомобиль укладывается в отведенное время (330 мин.). Задача 3. Оптимизация развозочного маршрутаИспользуя метод приращения расстояний, рассчитать оптимальный кольцевой развозочный маршрут по следующим данным: грузоподъёмность автомобиля – 10 т., статистический коэффициент использования грузоподъёмности – 0,8. Остальные данные представлены в табл. 1,2. Таблица 1 Объёмы поставок, т.
Таблица 2 Таблица расстояний, км.
Решение: I этап. Строим кратчайшую сеть, связывающую все пункты без замкнутых контуров по принципу минимизации расстояний между двумя пунктами (рис. 5). Расстояние L/=3+8+10+3+4+5+10+5=48 км. Е 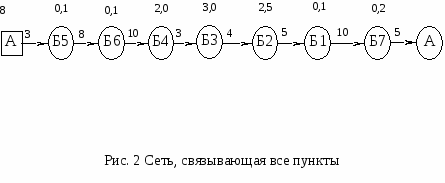 сли есть равные кратчайшие расстояния (например от пункта А до пункта Г – 3 км. и от пункта А до пункта Б – 3 км.), то таких сетей может быть несколько, в этом случае каждая должна быть построена и для каждой рассчитывается расстояние, затем выбирается наименьшее расстояние и соответствующая цепь считается базовой. II этап. По каждой ветви сети, начиная с пункта, наиболее удалённого от начального пункта А, группируем пункты на маршрут (табл. 3) с учётом количества ввозимого груза и грузоподъёмности единицы подвижного состава. Масса перевозимого груза за один раз рассчитывается: q*КСИГ=10*0,8= 8 т.=8000 кг. Таблица 3 Группировка маршрутов исходя из грузоподъёмности автомобиля
III этап. Определение рационального порядка объезда пунктов. Для этого строится таблица-матрица (табл. 4), в которой по диагонали размещены пункты, включаемые в маршрут, и начальный пункт А, а в соответствующих клетках – кратчайшее расстояние между ними. Таблица 4 Матрица для определения рационального порядка объезда пунктов первого маршрута
IV этап. Начальный маршрут строим для шести пунктов матрицы: первый и последний – пункт А, остальные выбираются из матрицы по максимальной сумме: «79»; «55» соответственно начальный маршрут имеет вид: А – Б6 – Б1 – А. Для включения оставшихся пунктов в маршрут выбираем из них тот, которому соответствует следующая наибольшая сумма – «50». таких цифр две и выбираем любой пункт соответствующий этой сумме, т. е. Б3 или Б2. Выбираем пункт Б3. Необходимо решить между какими пунктами должен быть расположен пункт Б3, т. е. между пунктами А и Б6, между пунктами Б6 и Б1 или между пунктами Б1 и А. Для этого рассчитывается приращение:  А-Б3-Б6=LАБ3+LБ3Б6-LАБ6=9+13-11=11 км.Б6-Б3-Б1=LБ6Б3+LБ3Б1-LБ6Б1=13+9-12=10 км.Б1-Б3-А=LБ1Б3+LБ3А-LБ1А=9+9-6=12 км.Минимальное значение соответствует Б6-Б3-Б1, следовательно пункт Б3 должен быть расположен между пунктами Б6 и Б1.Получаем маршрут вида: А – Б6 – Б3 – Б1 – А. Б2? А-Б2-Б6=LАБ2+LБ2Б6-LАБ6=11+14-11=14 км.Б6-Б2-Б3=LБ6Б2+LБ2Б3-LБ6Б3=14+4-13=5 км.Б3-Б2-Б1=LБ3Б2+LБ2Б1-LБ3Б1=4+5-9= 0 км.Б1-Б2-А=LБ1Б2+LБ2А-LБ1А=5+11-6=10 км.Пункт Б2 должен находится между пунктами Б3 и Б1. А – Б6 – Б3 – Б2 – Б1 – А. Б5 - ? А-Б5-Б6=LАБ5+LБ5Б6-LАБ6= 3+8-11= 0 км.Б6-Б5-Б3=LБ6Б5+LБ5Б3-LБ6Б3=8+8-13=3 км.Б3-Б5-Б2=LБ3Б5+LБ5Б2-LБ3Б2=8+7-4= 11 км.Б2-Б5-Б1=LБ2Б5+LБ5Б1-LБ2Б1=7+4-5=6 км.Б1-Б5-А=LБ1Б5+LБ5А-LБ1А=4+3-6=1 км.Пункт Б5 должен находится между пунктами А и Б6. А – Б5 – Б6 – Б3 – Б2 – Б1 – А Б7 - ? А-Б7-Б5=LАБ7+LБ7Б5-LАБ5=5+8-3 = 10 км.Б5-Б7-Б6=LБ5Б7+LБ7Б6-LБ5Б6=8+11-8=11 км.Б6-Б7-Б3=LБ6Б7+LБ7Б3-LБ6Б3=11+4-13= 2 км.Б3-Б7-Б2=LБ3Б7+LБ7Б2-LБ3Б2=4+5-4=5 км.Б2-Б7-Б1=LБ2Б7+LБ7Б1-LБ2Б1=5+10-5=10 км.Б1-Б7-А=LБ1Б7+LБ7А-LБ1А=10+5-6=9 км.Пункт Б7 должен находится между пунктами Б6 и Б3. А – Б5 – Б6 –Б7 – Б3 – Б2 – Б1 – А. Б4 - ? А-Б4-Б5=LАБ4+LБ4Б5-LАБ5= 6+9-3= 12 км.Б5-Б4-Б6=LБ5Б4+LБ4Б6-LБ5Б6=9+10-8=11 км.Б6-Б4-Б7=LБ6Б4+LБ4Б7-LБ6Б7=10+1-11= 0 км.Б7-Б4-Б3=LБ7Б4+LБ4Б3-LБ7Б3=1+3-4=0 км.Б3-Б4-Б2=LБ3Б4+LБ4Б2-LБ3Б2=3+4-4=3 км.Б2-Б4-Б1=LБ2Б4+LБ4Б1-LБ2Б1=4+9-5=8 км.Б1-Б4-А=LБ1Б4+LБ4А-LБ1А=9+6-6= 9 км.Пункт Б4 должен находится между пунктами Б6 и Б7. Окончательный вид маршрута имеет вид: А – Б5 – Б6 –Б4 – Б7 – Б3 – Б2 – Б1 – А. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
,
