1. Запишите формулы представления сигнала в виде ряда Фурье в вещественной и комплексной формах
 Скачать 0.54 Mb.
|
|
1. Запишите формулы представления сигнала в виде ряда Фурье в вещественной и комплексной формах. Вещественная форма ряда Фурье:  , где  Комплексная форма ряда Фурье:  .2. Что такое амплитудный и фазовый спектры периодического сигнала?  .Это представление называют вещественной формой ряда Фурье. Совокупность  и коэффициентов  образуют амплитудный, а совокупность  - фазовый спектры периодического сигнала  .3. Комплексный коэффициент  на некоторой положительной частоте равен  . Какой смысл имеют коэффициенты 1,5 и?1,5 – половина амплитуды гармоники на частоте  . - начальная фаза соответствующей гармонике.4. Как выражается связь между спектральной функцией одиночного импульса  и комплексной амплитудой  ряда Фурье, описывающего периодическую последовательность, составленную из таких импульсов? 5. У периодического сигнала изменилась полярность. Что произойдет с его АС и ФС? АС – останется без изменения ФС получает добавку равную  на каждой частоте. , 6. Если сигнал является периодическим, то спектр его дискретен. Справедливо ли обратное утверждение? В общем случае НЕТ. 7. Приведите формулы прямого и обратного преобразования Фурье. При каких условиях можно пользоваться формулой прямого преобразования Фурье? Прямое:  Обратное:  Сигнал s(t) должен удовлетворять условиям Дирихле: Не имеет разрывов 2-го рода (с уходящими в бесконечность ветвями функции); Имеет конечное число разрывов 1-о рода; Имеет конечное число экстремумов; Требование абсолютной интегрируемости сигнала:  8. Какой физический смысл имеют модуль и аргумент спектральной функции непериодического сигнала? Спектральную функцию можно представить в показательной форме:   Физический смысл спектральной функции: Сигнал s(t) представляется в виде суммы бесконечно большого числа гармонических составляющих с бесконечно малыми амплитудами  , непрерывно заполняющих интервал частот от 0 до  ; начальные фазы этих составляющих заданы функцией  , а частотная зависимость “плотности” бесконечно малых амплитуд описывается функцией  .9. Спектральная функция  непериодического сигнала на некоторой положительной частоте равен . Какой смысл имеют коэффициенты 1,5 и?1,5 – весовой коэффициент.  - фаза10. Как изменится спектральная функция при умножении сигнала S(t) на  ? Умножение видеоимпульса на гармоническую функцию в спектральной области приводит к смещению спектра видеоимпульса влево и вправо на величину  .  .11. Как изменится амплитудный и фазовый спектры сигнала при его запаздывании? Пусть сигналу s(t) соответствует спектральная функция 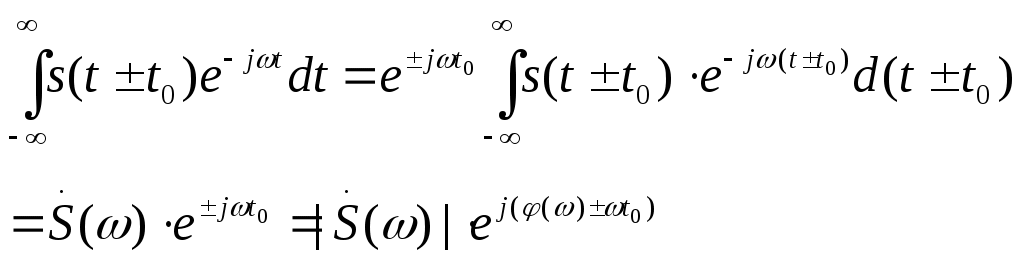. Найдем преобразование Фурье сдвинутого во времени сигнала,  : При сдвиге сигнала на временной интервал  амплитудный спектр сигнала не изменится, в фазовом спектре сигнала появляется дополнительная компонента  . 12. Как выражается спектральная функция произведения двух функций, если известны спектральные плотности сомножителей? (Привести формулу). Пусть f(t) и g(t) – сигналы со спектральными функциями 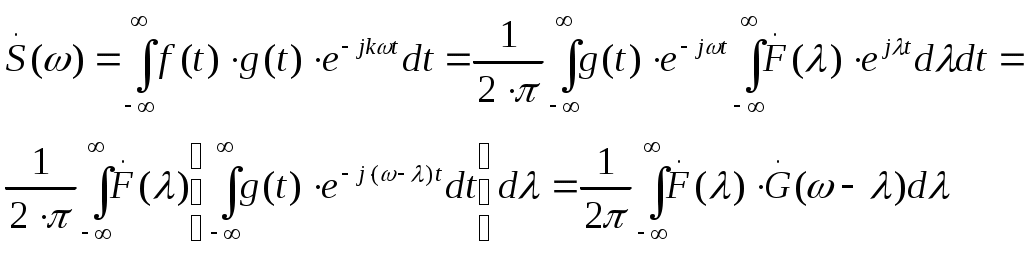 и  соответственно. Тогда сигналу s(t)=f(t)∙g(t) соответствует спектральная функция: Спектральная функция произведения сигналов есть свертка их спектральных функций (с коэффициентом 1/(2π)) 13. В чем заключается фильтрующее свойство δ-функции?  .15. Дайте определение и перечислите основные свойства корреляционной функции детерминированного сигнала. Как она связана со спектром сигнала?  Свойства:     Связь КФ сигнала с его энергетическим спектром:  16. Зависит ли форма корреляционной функции детерминированного сигнала от фазового спектра этого сигнала? Почему? Нет, так как .17.Перечислите особенности корреляционной функции периодического сигнала? КФ непрерывного и периодического сигнала определяют по формуле:  КФ периодического сигнала сама является периодической функцией и имеет размерность мощности. Значение B(0)=Мощности сигнала. 18. Как определяется мгновенная мощность, энергия и средняя мощность сигнала s(t) на интервале времени [t1, t2]? Мгновенная удельная мощность сигнала:  Удельная энергия: 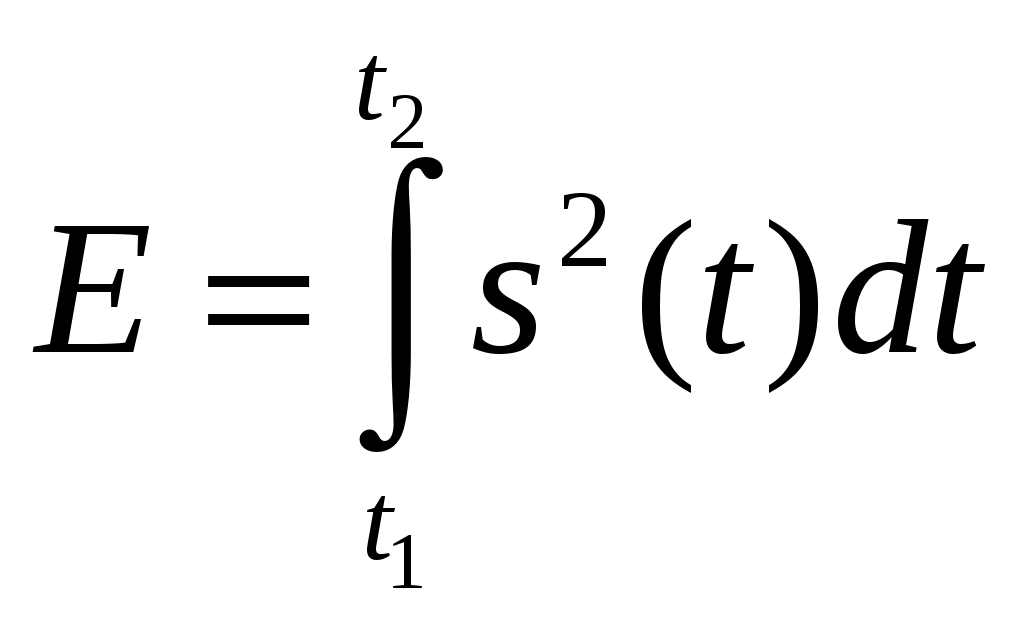 Средняя удельная мощность:  12. Как выглядит спектр АМ-колебаний при модуляции: Гармоническим колебанием; Произвольным периодическим сигналом? АМ-колебаний при модуляции Гармоническим колебанием:  АМ-колебаний при модуляции произвольным периодическим сигналом: Принято называть  несущей,  - верхней боковой,  - нижней боковой частотами.Однотональная модуляция:  Спектр  Многотональная модуляция: спектр  20. Какой вид имеет векторная диаграмма АМ колебания при гармонической модуляции?  21. Запишите общее выражение для колебаний с угловой модуляцией. Какими соотношениями связаны полная фаза и мгновенная частота колебаний? Модель радиосигнала с угловой модуляцией:   - мгновенная частота - полная фаза22. Дайте определение понятиям ЧМ и ФМ. В чем заключаются сходства и различая между ними? ФМ:  , где  ЧМ:  , где  - полная фазаЛегко заметить, что частотная и фазовая модуляции тесно связаны, а именно, если модулирующая функция представлена, как ks(t), то ЧМ при  соответствует ФМ по закону  ; ФМ при  соответствует ЧМ по закону  .23. Какой физический смысл имеют понятия “девиация фазы” и “девиация частоты” при угловой модуляции. Дайте определение "индексу угловой модуляции” β? Девиация фазы – амплитуда отклонения фазы от линейного закона. Девиация частоты – амплитуда отклонения частоты от несущей.  - при частотной модуляции - при фазовой модуляции24. По каким приближенным формулам можно определить эффективную ширину спектра колебания с гармонической угловой модуляцией в случае β<<1 и β>>1? При β>>1 эффективная ширина спектра сигнала с гармонической УМ равняется удвоенной девиации частоты:  .При β<<1 эффективная ширина спектра сигнала с гармонической УМ равняется удвоенной частоте модуляции:  .25. Чем отличаются спектральные и векторные диаграммы АМ и ЧМ колебаний при малой глубине модуляции? ВД АМ - ВД УМ -  АМ: АС - ФС - 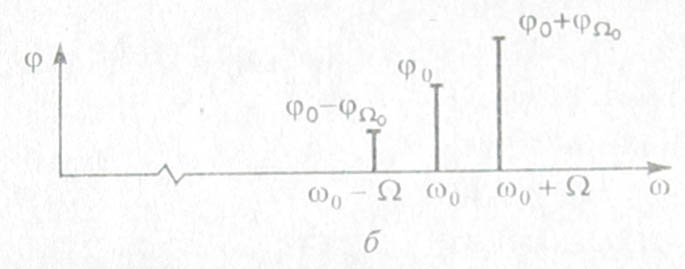 УМ: АС - ФС - 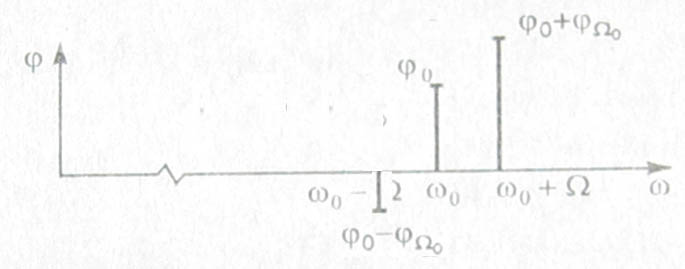 26. Привести графики амплитудных спектров периодических последовательностей прямоугольных видео- и радио импульсов? АС видеоимпульса -  АС радиоимпульса - 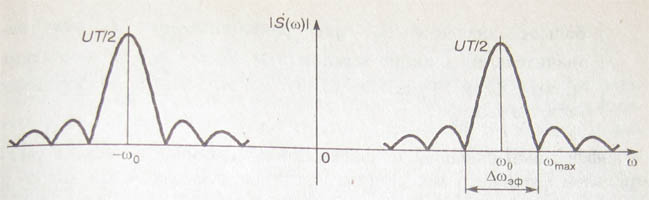 27. Запишите выражения, соответствующие прямому и обратному преобразованиям Гильберта. Что должны представлять собой цепи, реализующие данные преобразования? Прямое преобразование Гильберта:  Обратное преобразование Гильберта:   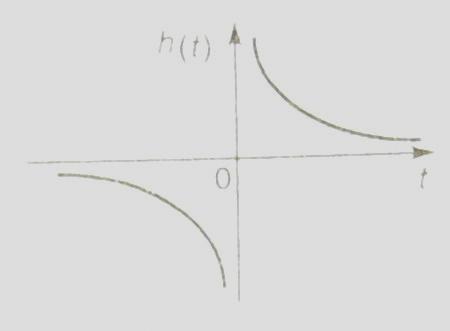  28. Какие сигналы называются случайными? Что является наиболее полной характеристикой случайного сигнала? Можно ли считать реализацию случайного процесса случайным сигналом? Случайный процесс (сигнал) X(t) – это функция особого вида, характеризующаяся тем, что значения, принимаемые ею в любой момент времени t, являются случайными величинами. Полное описание случайного процесса дает его ансамбль реализаций. До регистрации (до приема) случайный сигнал следует рассматривать именно как случайный процесс, представляющий собой совокупность (ансамбль) функций времени  , подчиняющихся некоторой общей для них статистической закономерности. Одна из этих функций, ставшая полностью известной после приема сообщения, называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени.29. Запишите выражения для статистических характеристик случайного процесса, связанных с одномерной плотностью вероятности. Функция распределения:  .Одномерная плотность вероятности:  . Математическое ожидание:  ;  .Дисперсия:  Среднее квадратическое отклонение:  30. Перечислите основные свойства плотности вероятности и функции распределения вероятностей случайной величины.  является неубывающей функцией, значения которой лежат в диапазоне  . Для предельных значений x выполняются следующие соотношения:  и  .Плотность вероятности является неотрицательной функцией:  .Вероятность попадания значения случайного процесса в интервал (a,b] равна разности значений функции распределения на концах этого интервала:  .Чтобы рассчитать вероятность попадания значения  в произвольный интервал [a,b], необходимо вычислить следующий интеграл:  .Так как случайная величина обязательно принимает какое-нибудь значение, то должно выполняться условие нормировки:  . Зная плотность вероятности, можно рассчитать и функцию распределения:  .31. Что такое ковариационная и корреляционная функция случайного процесса? Как они связаны между собой? Ковариационная функция случайного процесса X(t) представляет собой статистически усредненное произведение значений случайной величины X(t) в моменты времени  и  : .  .Корреляционная функция представляет собой статистически усредненное произведение значений центрированной случайной функции  в моменты времени и : .  .32. Дайте определения случайных процессов, стационарных в узком и широком смыслах? Стационарные случайные процессы – процессы, статистические характеристики которых одинаковы во всех временных сечениях. Стационарный в узком смысле - его многомерная плотность вероятности  произвольной размерности n не изменяется при одновременном сдвиге всех временных сечений  вдоль оси времени на одинаковую величину τ:  при любом τ.Если же ограничить требования тем, чтобы от временного сдвига не зависели лишь одномерная и двумерная плотности вероятности, то такой случайный процесс будет стационарен в широком смысле. 33. Что такое эргодический случайный процесс? Стационарный случайный процесс называется эргодическим, если при определении любых его статистических характеристик усреднение по множеству (ансамблю) реализаций эквивалентно усреднению по времени одной, теоретически бесконечно длинной, реализации. 34. Запишите выражение для плотности вероятности стационарного нормального случайного процесса. Дайте формулировку центральной предельной теоремы. 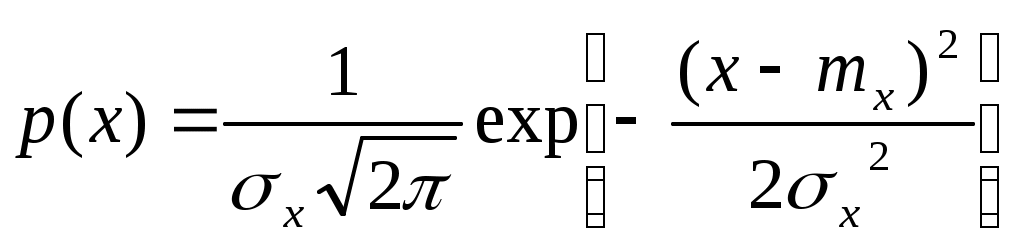 .При суммировании достаточно большого числа равномощных статистически независимых случайных величин, имеющих произвольные плотности распределения вероятности, плотность распределения суммы стремится к нормальной. 35. Что такое интервал корреляции случайного процесса? Как он вычисляется? В какой связи он находится с эффективной шириной спектра? Количественной характеристикой, служащей для оценки “скорости изменения” реализаций случайного процесса, является интервал корреляции  , определяемый как .Величины и  связаны соотношением неопределенности: .36. Почему понятие комплексного спектра не используют в отношении случайного процесса? Среднее значение спектральной плотности случайного процесса:  .Как видно из формулы, усредненная спектральная плотность случайного процесса представляет собой спектр его детерминированной составляющей (математического ожидания). Для центрированных процессов  и  . Таким образом, усредненное значение спектральной плотности не несет никакой информации о случайной составляющей процесса. Это говорит о том, что фазы спектральных составляющих в различных реализациях процесса случайны и независимы.37. Что такое спектральная плотность мощности случайного процесса? Какова ее размерность? Сформулируйте теорему Винера-Хинчина. Спектральная плотность мощности:  .В2*с Теорема: Корреляционная функция случайного процесса и его спектральная плотность мощности связаны друг с другом преобразованием Фурье:  .38. Что такое “белый шум”? Каковы его дисперсия и функция корреляции? Осуществим ли реально сигнал такого вида? В радиотехнике белым шумом называют стационарный случайный процесс, спектральная плотность мощности которого постоянна на всех частотах:  .Согласно теореме Винера-Хинчина корреляционная функция белого шума представляет собой дельта функцию:  . Дисперсия белого шума бесконечно велика. Белый шум является абстрактной математической моделью и физически существовать не может. Это объясняется прежде всего бесконечностью его дисперсии (т.е. средней мощности). 39. Каковы основные характеристики линейной цепи во временной и спектральной областях? Как они связаны между собой? Почему? Импульсная характеристика: реакция цепи на элементарный входной импульс – дельта функцию;  .Переходная характеристика: реакция цепи на воздействие в виде единичного скачка;  .   . Комплексный коэффициент передачи: преобразование Фурье импульсной характеристики цепи.  . 40. Как связаны детерминированные сигналы на входе и выходе линейной цепи во временной области?  .41. Как связаны энергетические спектры случайных процессов на входе и выходе линейной цепи?  42. Какую характеристику случайного процесса на выходе линейной цепи и как находят при временном подходе?  , где  - корреляционная функция импульсной характеристики цепи.43. Изобразите схемы и частотные характеристики простейших RC-фильтров нижних и верхних частот. ФНЧ:   ФВЧ:   44. Изобразите схемы, переходные и импульсные характеристики RC-фильтров нижних и верхних частот. ФНЧ:  ФВЧ:  45. Запишите выражение для входного сопротивления последовательного колебательного контура. Изобразите его АЧХ и ФЧХ.   45. Дайте определения текущему и мгновенному спектрам сигнала.  .  46. Запишите выражения для комплексного коэффициента передачи линейной цепи с обратной связью и дайте определения видам обратной связи.  .Положительная обратная связь  .Отрицательная обратная связь  .Реактивная обратная связь  Комплексная обратная связь все остальные случаи. 47. Какие характеристики усилителя улучшаются при использовании в нем отрицательной обратной связи? Стабильность коэффициента передачи. Коррекция частотной характеристики. Уменьшение искажений. 48. Какая линейная цепь называется устойчивой? Какие вам известны критерии устойчивости? Цепь называется устойчивой, если свободные колебания при любых начальных условиях являются затухающими. Система устойчива, если действительные части всех корней её характеристического уравнения отрицательны. Для устойчивости цепи необходимо, что бы полюсы передаточной функции лежали в левой полуплоскости комплексной переменной. |