
Вариант № 1
Дана спектральная плотность стационарного случайного процесса: 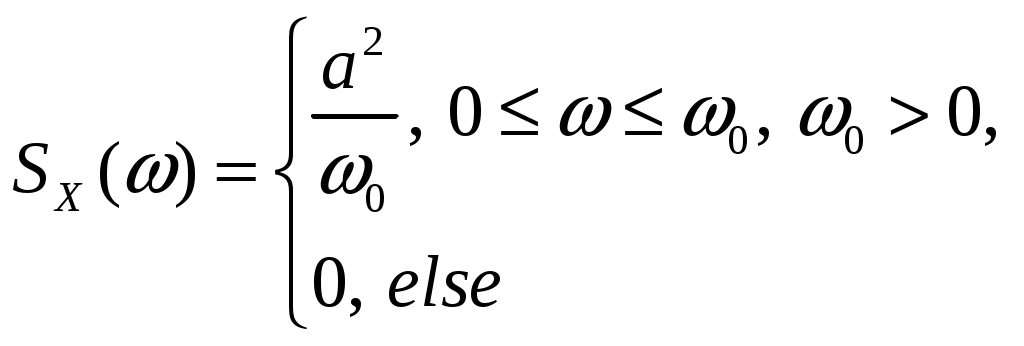 Определить автоковариационную функцию и дисперсию случайного процесса Определить автоковариационную функцию и дисперсию случайного процесса  . .
Вариант № 2
Дана автоковариационная функция стационарного случайного процесса:  . Определить спектральную плотность . Определить спектральную плотность  случайного процесса случайного процесса  . .
Вариант № 3
Дана спектральная плотность стационарного случайного процесса  : : 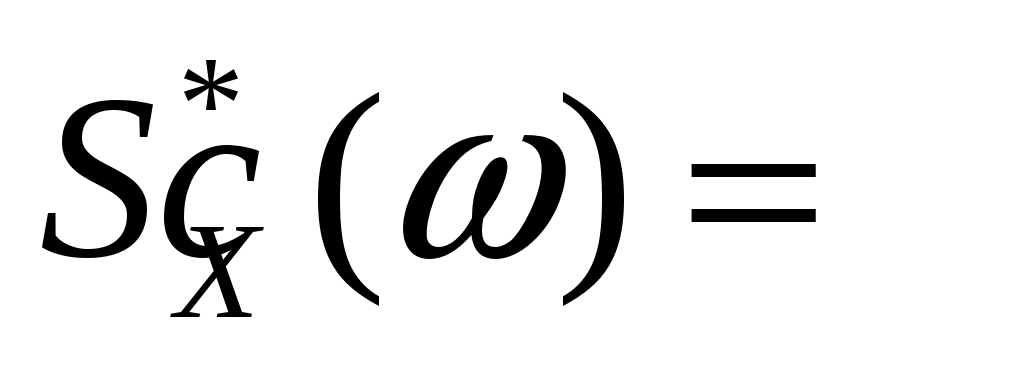 , ,  , , 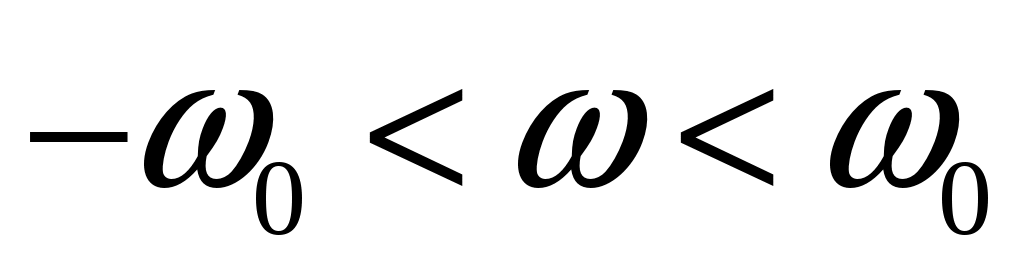 , , 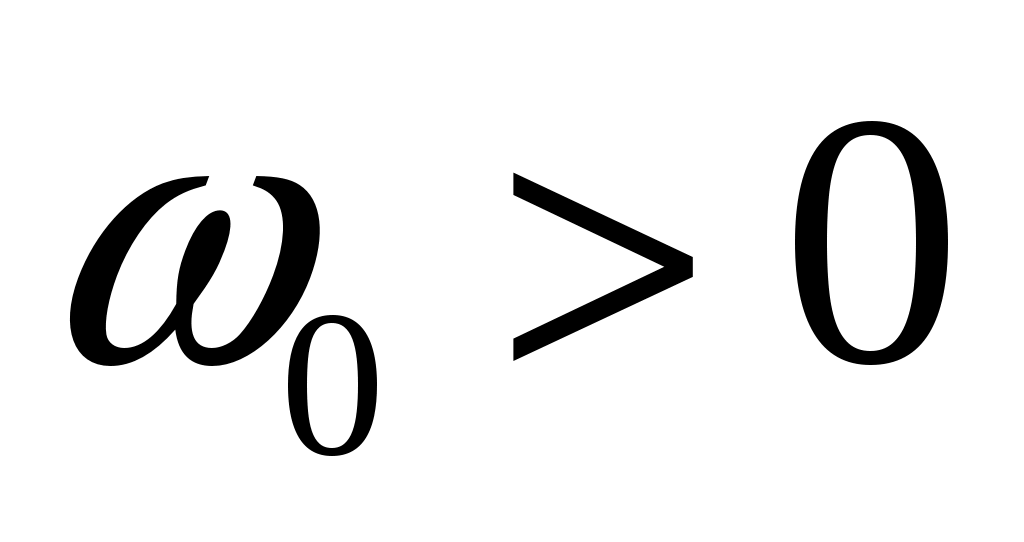 . Определить автоковариационную функцию . Определить автоковариационную функцию  стационарного процесса стационарного процесса  . .

Вариант № 4
Дана автоковариационная функция стационарного случайного процесса: 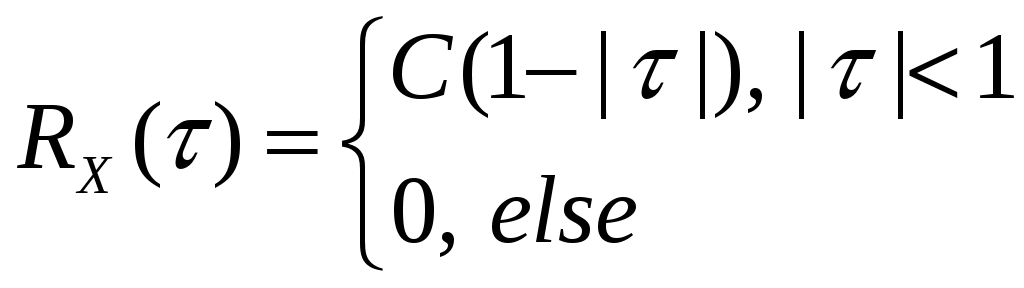 , , 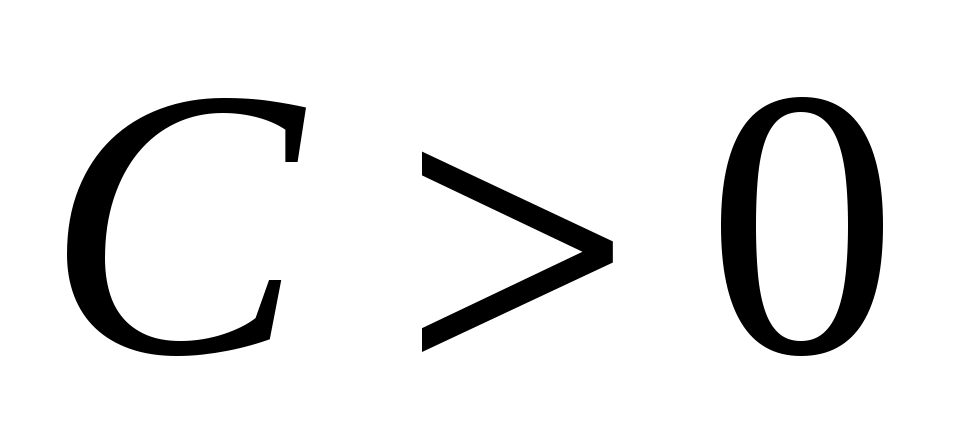 . Определить спектральную плотность . Определить спектральную плотность 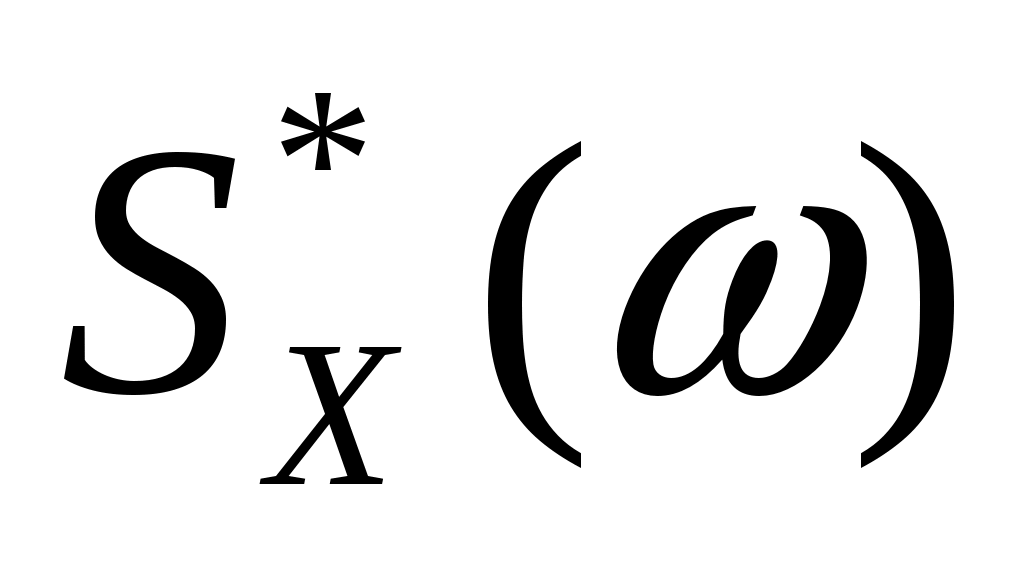 этого случайного процесса. этого случайного процесса.
Вариант № 5
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность 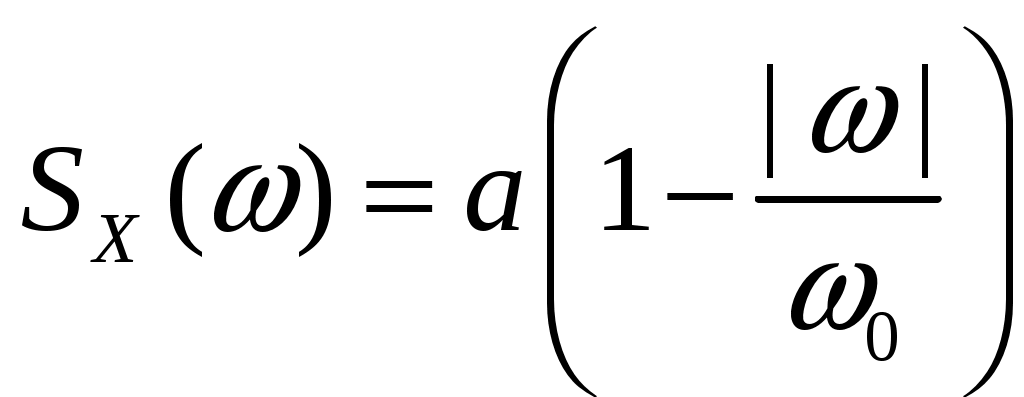 , ,  , , 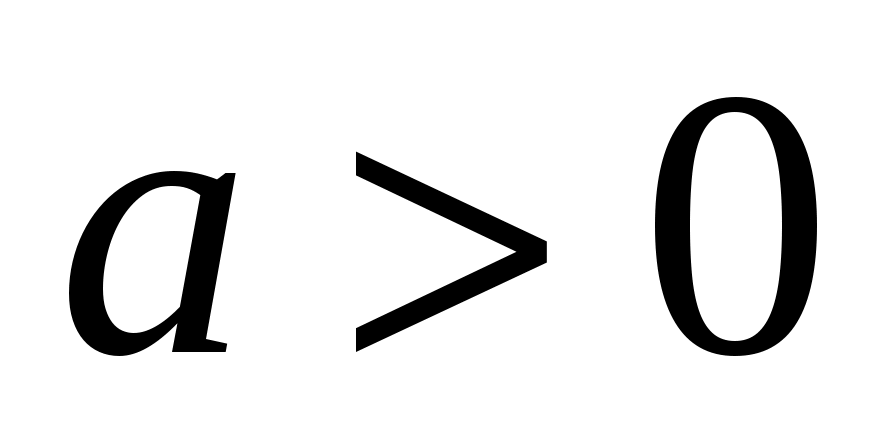 , , 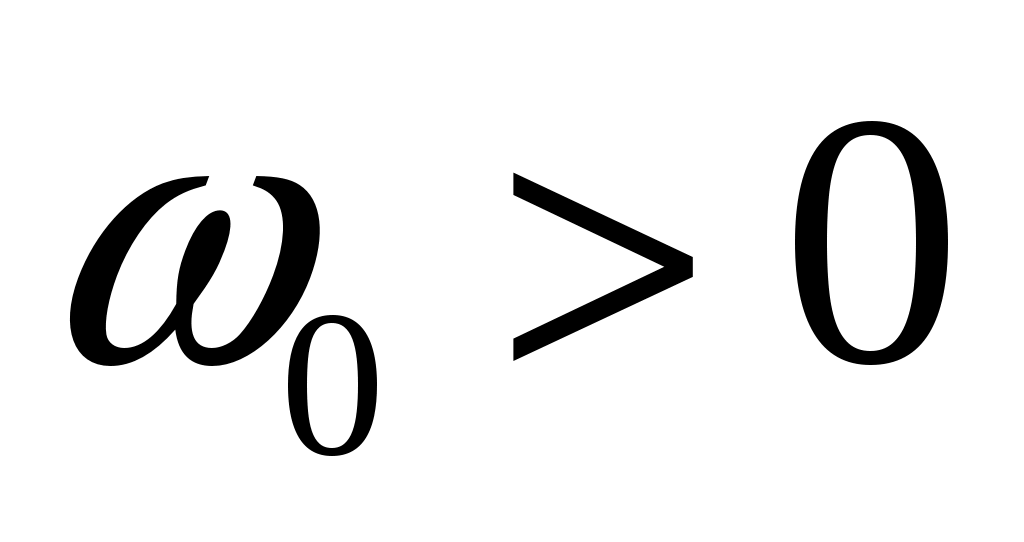 . Найти автоковариационную функцию случайного процесса . Найти автоковариационную функцию случайного процесса 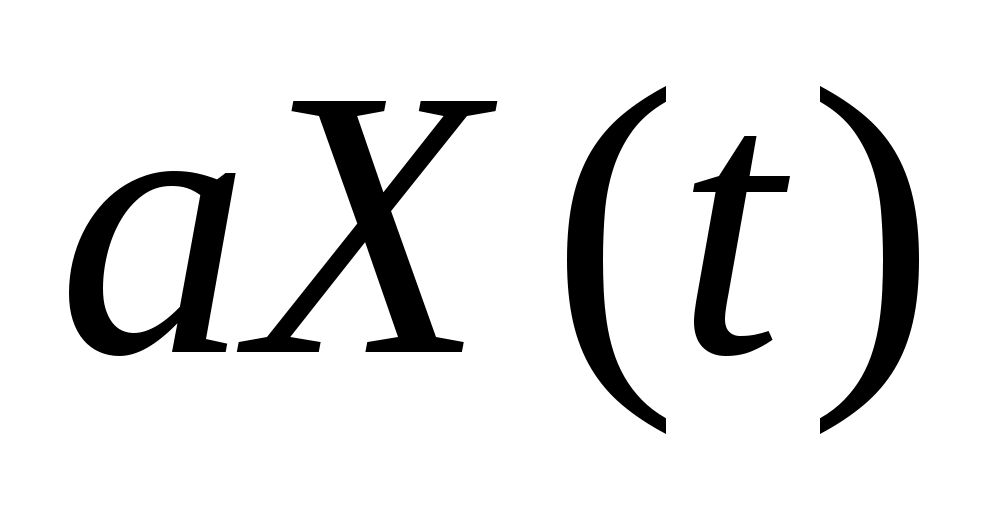 . .
Вариант № 6
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность  , ,  , , 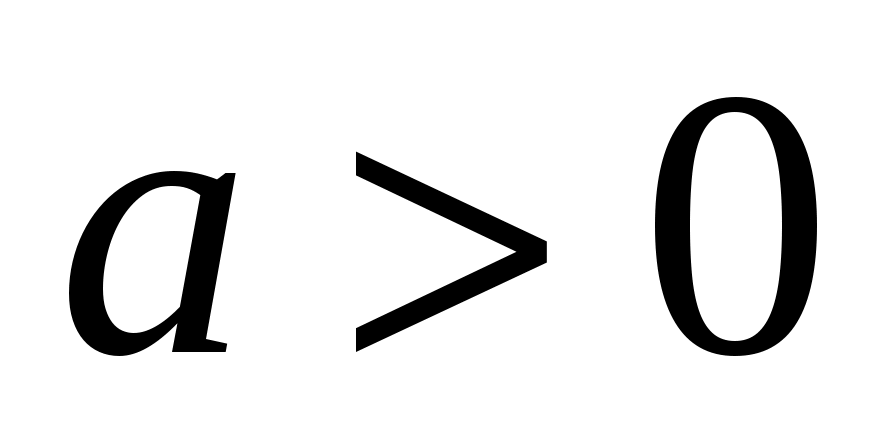 , , 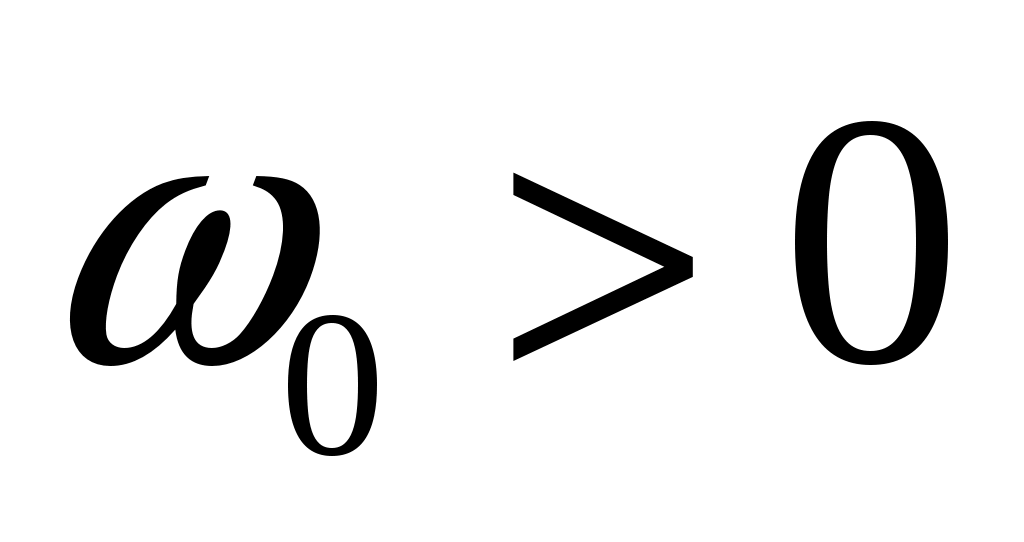 . Определить дисперсию случайного процесса . Определить дисперсию случайного процесса 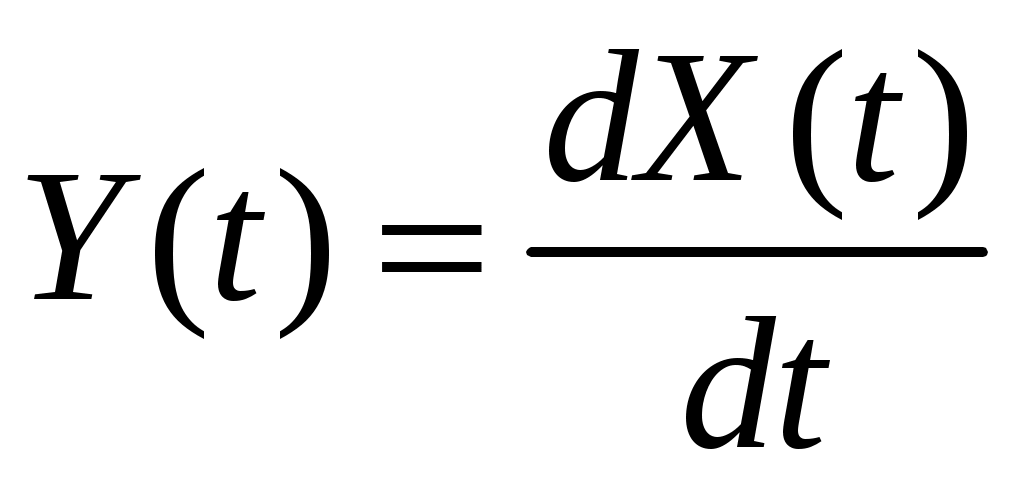 . .
Вариант № 7
Спектральная плотность 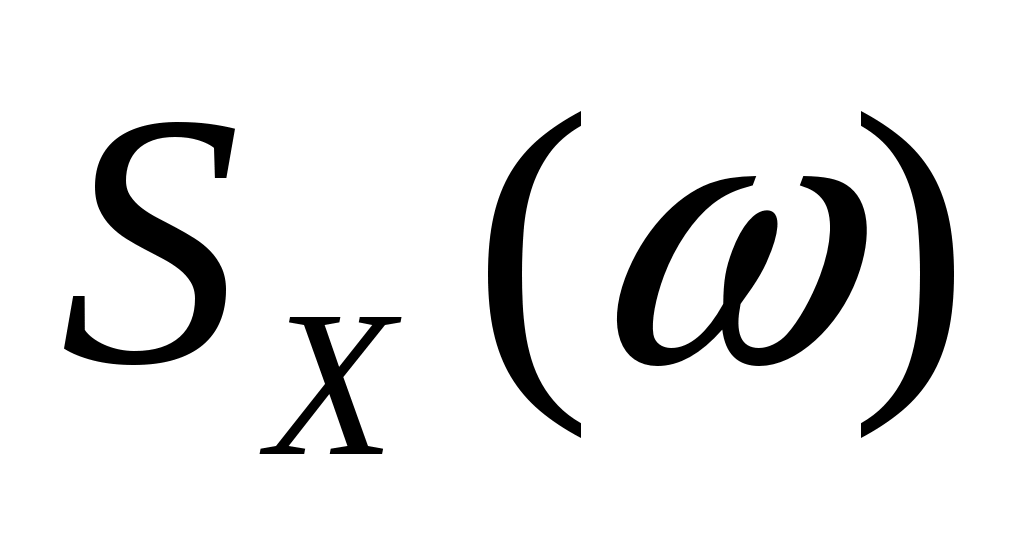 стационарного случайного процесса стационарного случайного процесса  имеет вид: имеет вид: 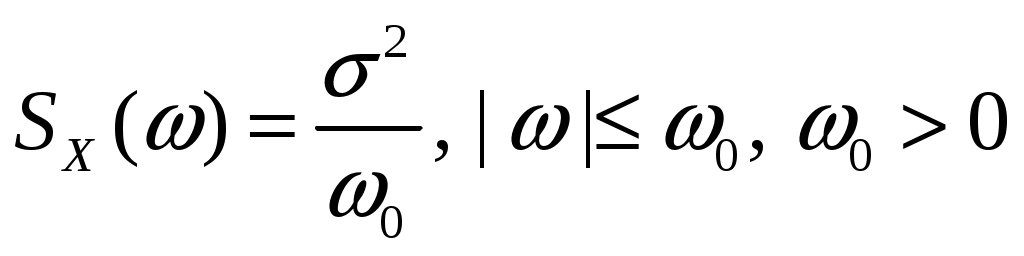 , Найти дисперсию случайного процесса , Найти дисперсию случайного процесса  . .
Вариант № 8
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию  . Найти автоковариационную функцию случайного процесса . Найти автоковариационную функцию случайного процесса  . .

Вариант № 9
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 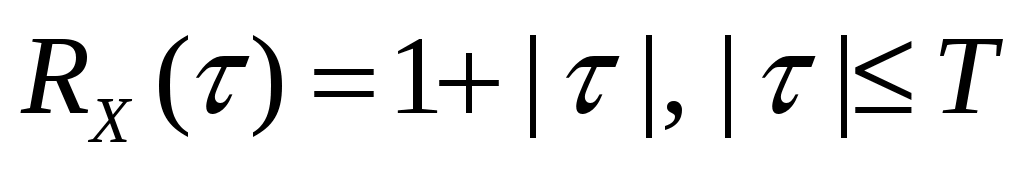 . Найти спектральную плотность случайного процесса . Найти спектральную плотность случайного процесса 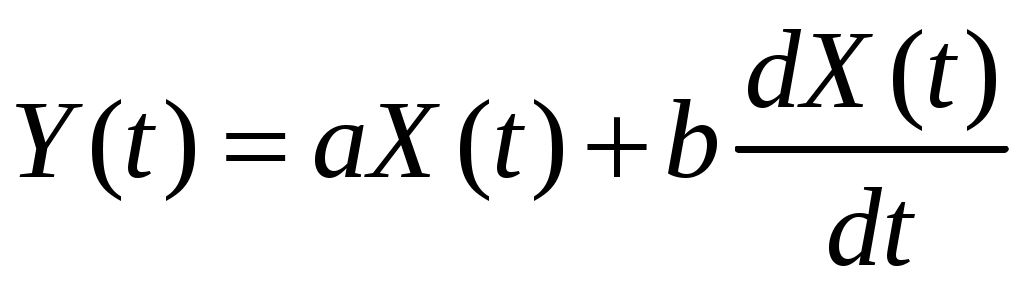 . .
Вариант № 10
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 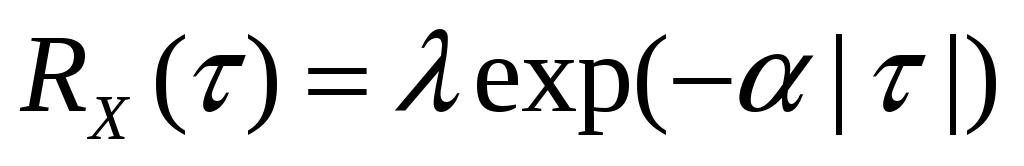 . Найти спектральную плотность . Найти спектральную плотность  случайного процесса случайного процесса 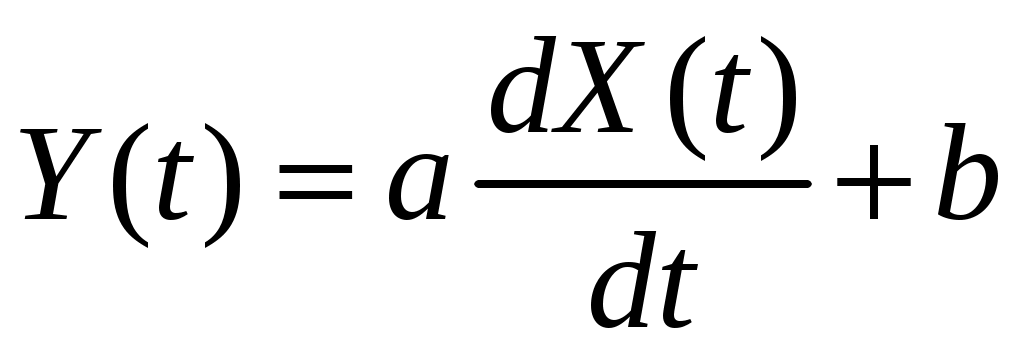 . .
Вариант № 11
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 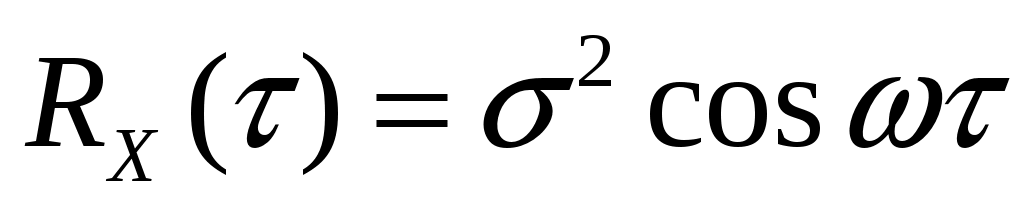 . Найти автоковариационную функцию случайного процесса . Найти автоковариационную функцию случайного процесса 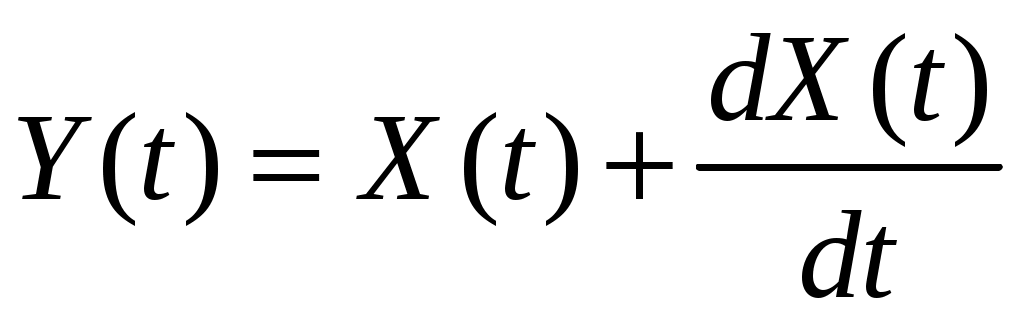 . .
Вариант № 12
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 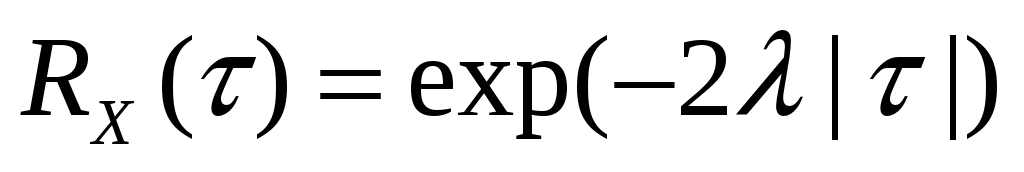 . Найти взаимную ковариационную функцию случайных процессов . Найти взаимную ковариационную функцию случайных процессов  и и  . .
Вариант № 13
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность 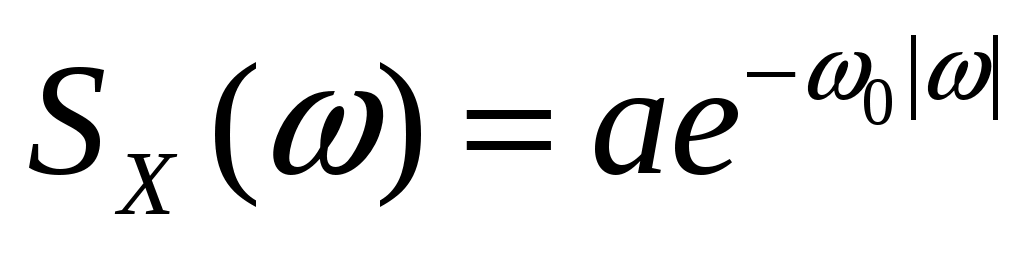 , , 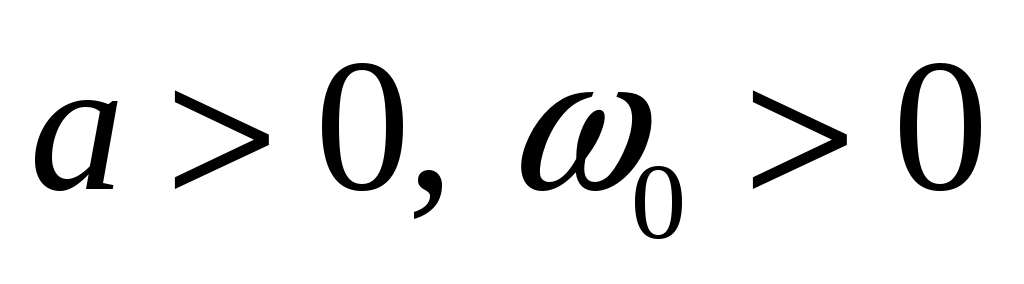 . Определить автоковариационную функцию . Определить автоковариационную функцию 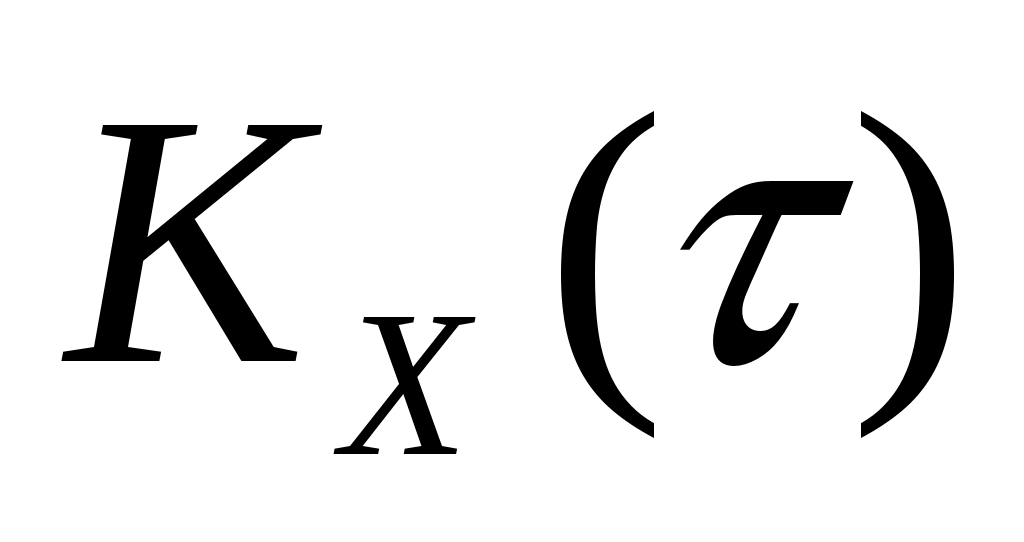 этого процесса. этого процесса.
Вариант № 14
Дана автоковариационная функция стационарного случайного процесса:  , , 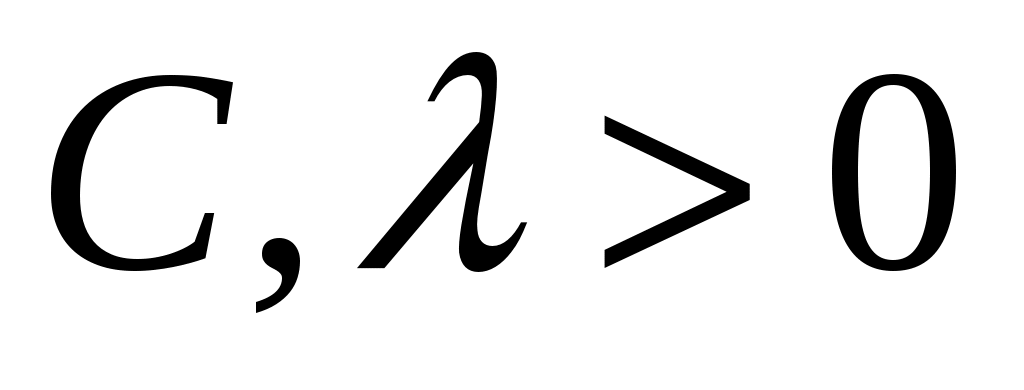 . Определить взаимную ковариационную функцию случайных процессов . Определить взаимную ковариационную функцию случайных процессов 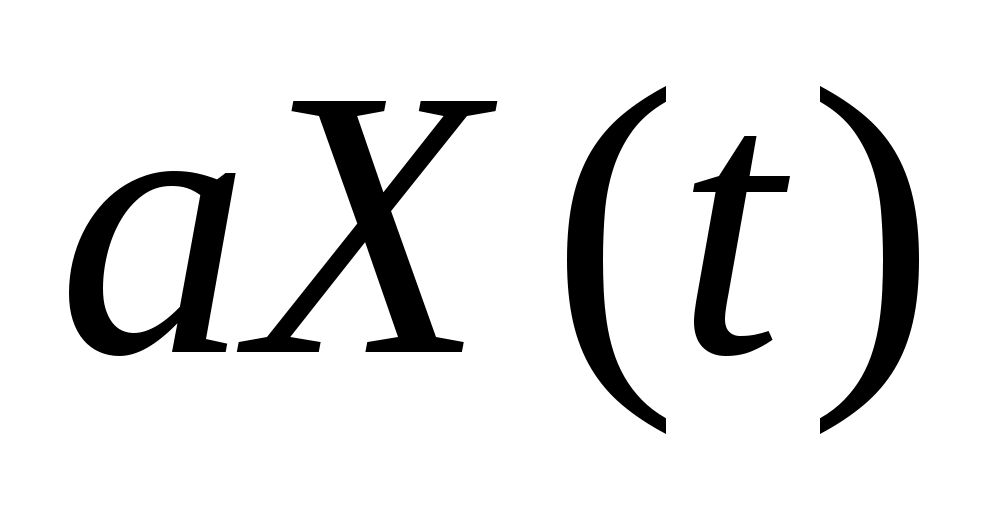 и и 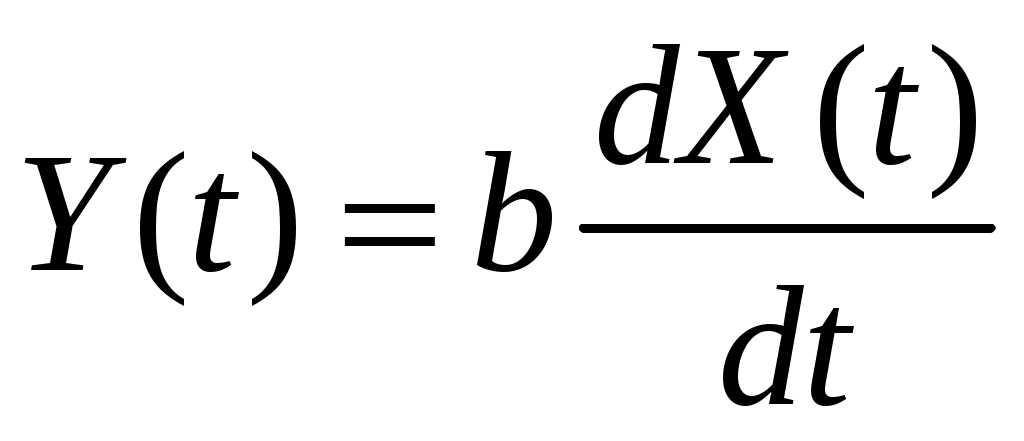 . .
Вариант № 15
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность  , , 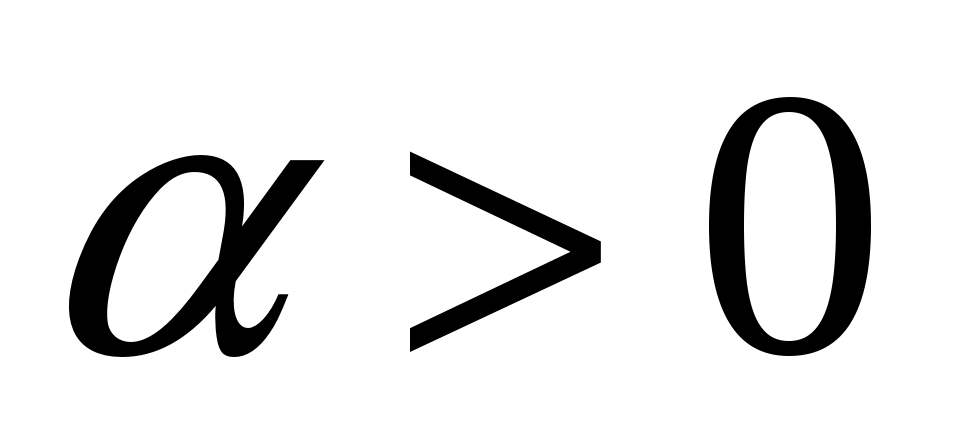 . Определить дисперсию случайного процесса . Определить дисперсию случайного процесса 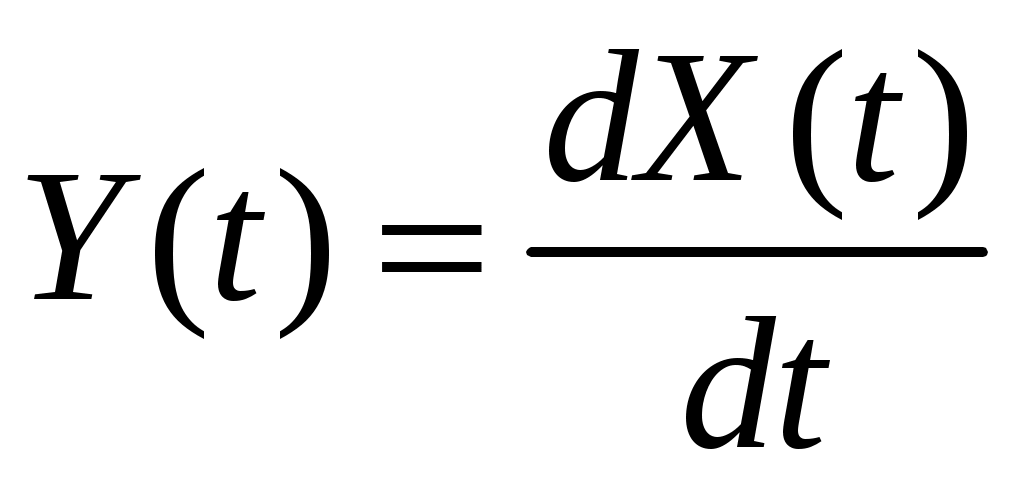 . .
Вариант № 16
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 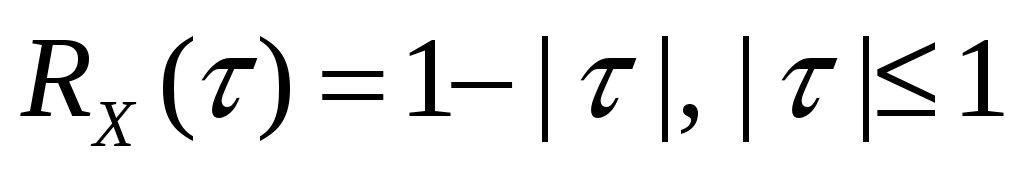 . Найти спектральную плотность случайного процесса . Найти спектральную плотность случайного процесса  . .

Вариант № 17
Спектральная плотность стационарного случайного процесса  имеет вид: имеет вид: 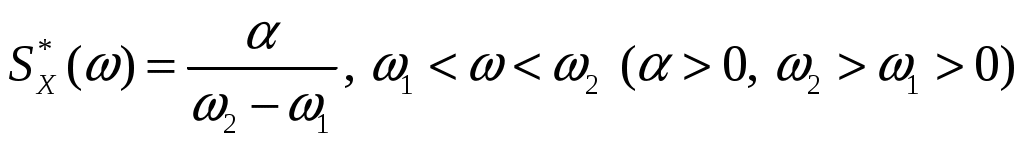 . Определить автоковариационную функцию и дисперсию случайного процесса . Определить автоковариационную функцию и дисперсию случайного процесса  . Какому случайному процессу соответствует предельный случай . Какому случайному процессу соответствует предельный случай 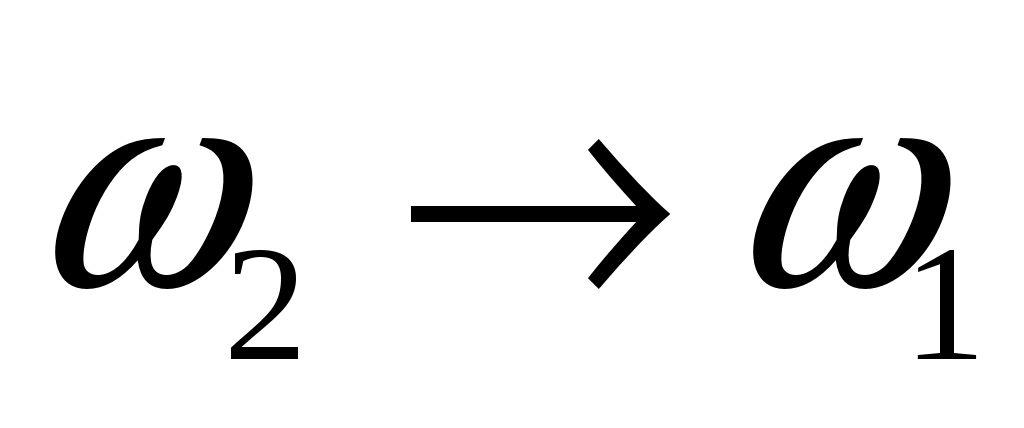 ? ?
Вариант № 18
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность 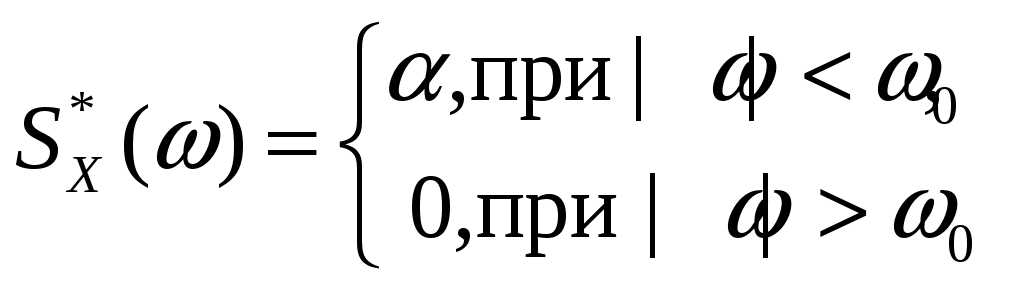 . Определить дисперсию . Определить дисперсию  и взаимную автоковариационную функцию случайных процессов и взаимную автоковариационную функцию случайных процессов  и и  . .
Вариант № 19
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность  , , 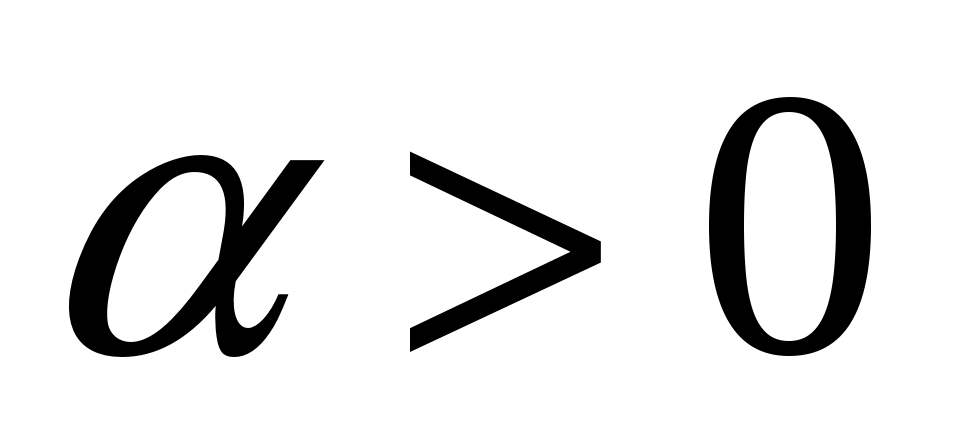 , , 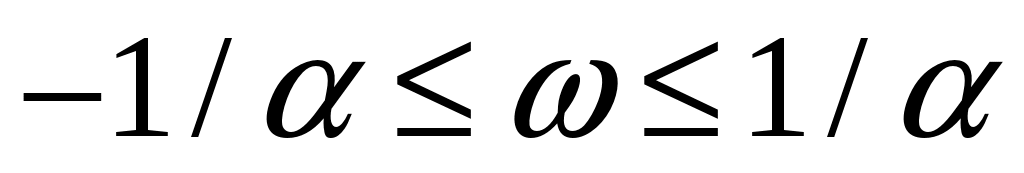 . Определить автоковариационную функцию случайного процесса . Определить автоковариационную функцию случайного процесса  . .
Вариант № 20
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 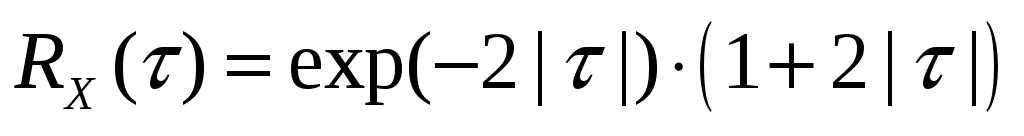 , , 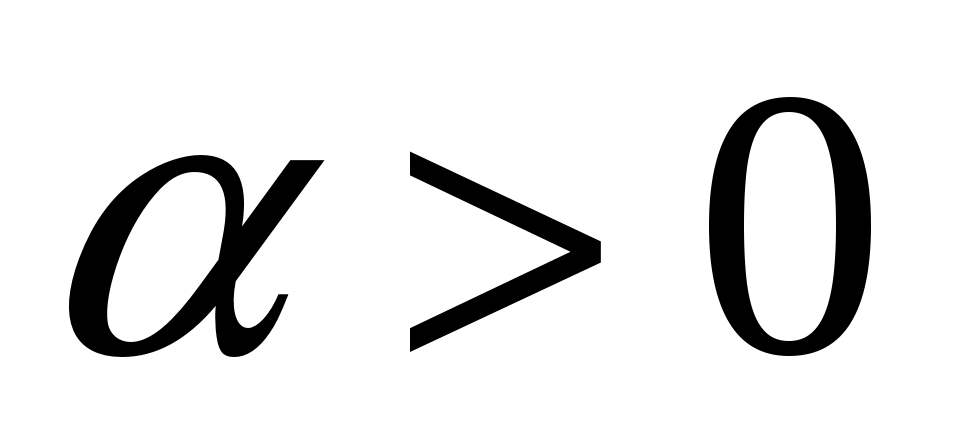 . Найти спектральную плотность и эффективную ширину спектра этой случайного процесса. . Найти спектральную плотность и эффективную ширину спектра этой случайного процесса.
Вариант № 21
Стационарный случайный процесс имеет спектральную плотность 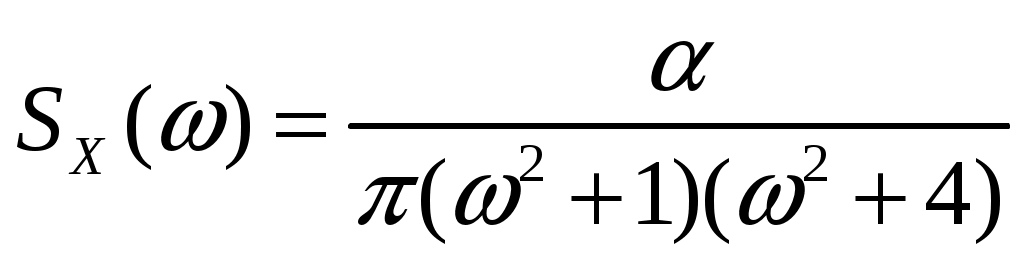 , ,  . Найти автоковариационную функцию случайного процесса . Найти автоковариационную функцию случайного процесса  . .
Вариант № 22
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность 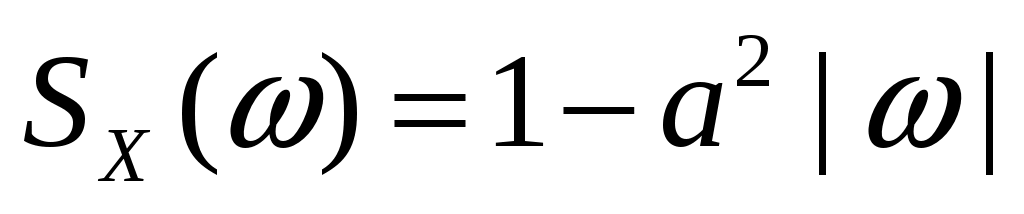 , , 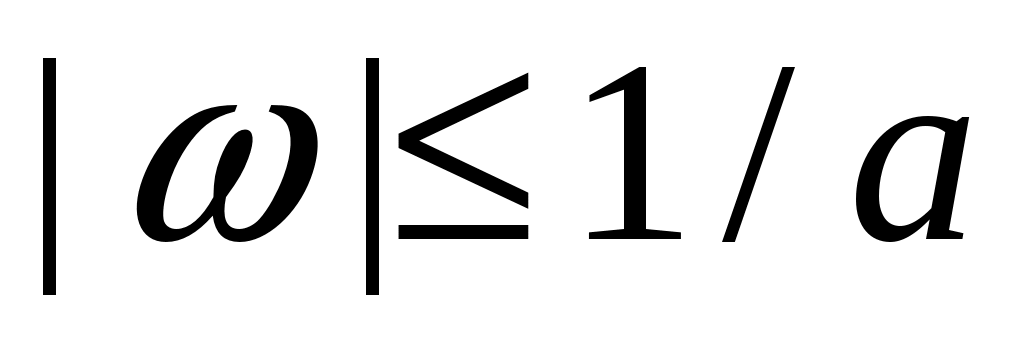 , , 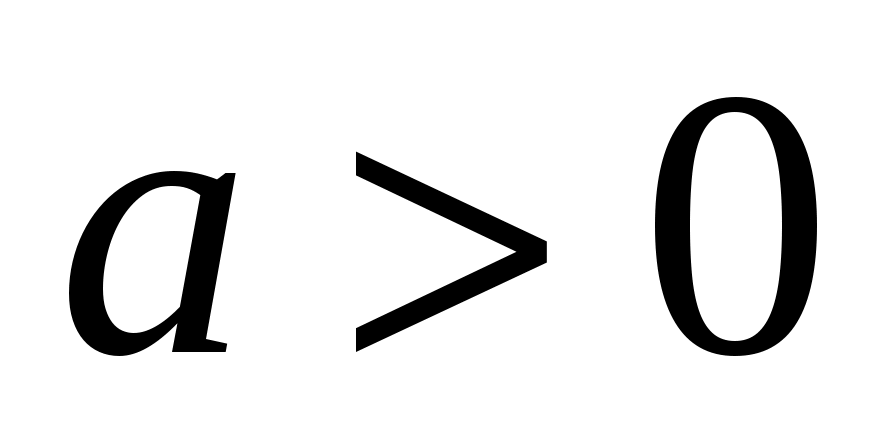 . Определить взаимную ковариационную функцию случайных процессов . Определить взаимную ковариационную функцию случайных процессов  и и 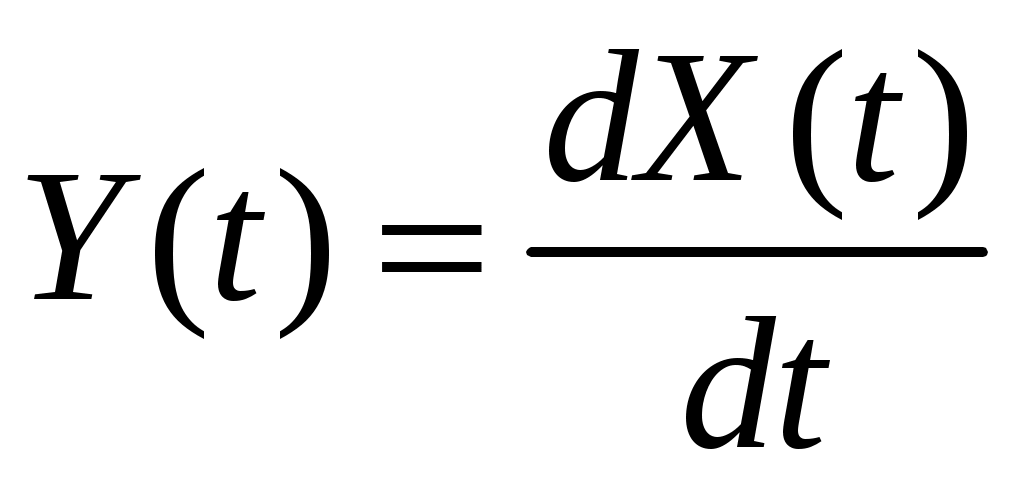 . .
Вариант № 23
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 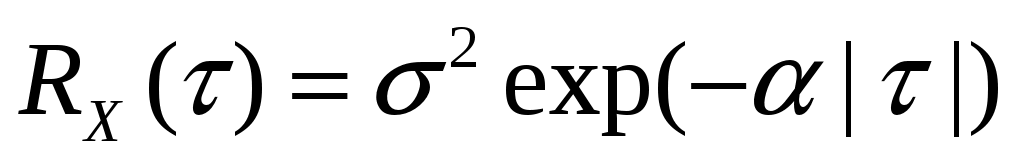 . Найти взаимную автоковариационную функцию случайных процессов . Найти взаимную автоковариационную функцию случайных процессов  и и 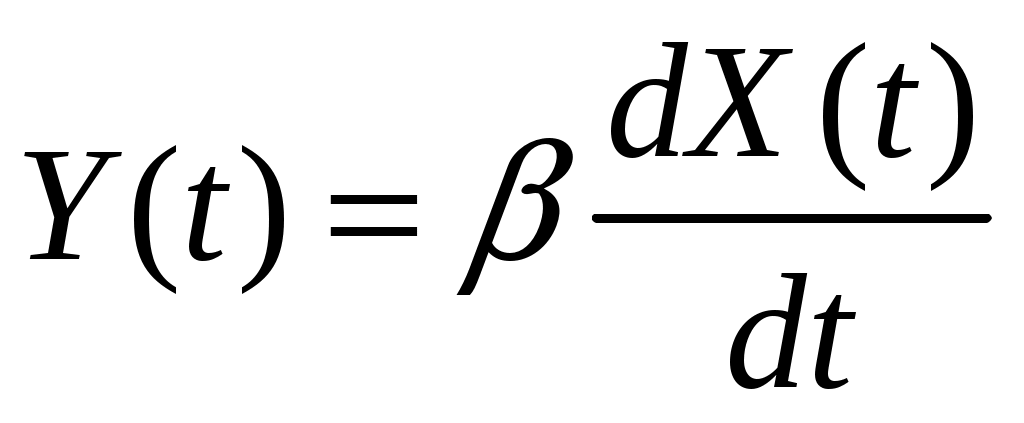 . .
Вариант № 24
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность 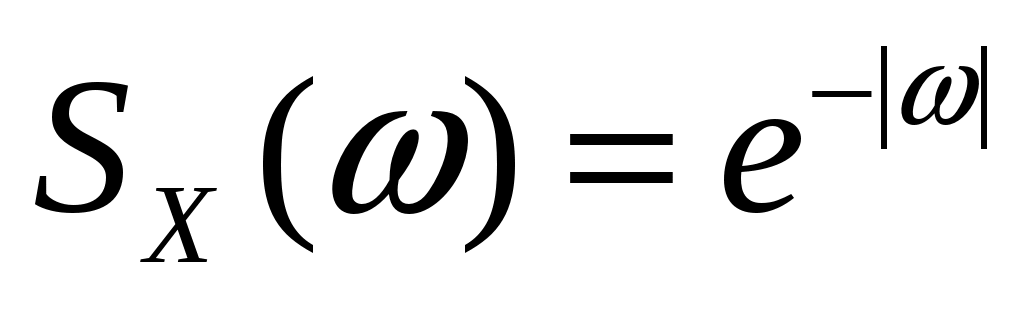 , ,  . Определить взаимную ковариационную функцию случайных процессов . Определить взаимную ковариационную функцию случайных процессов  и и 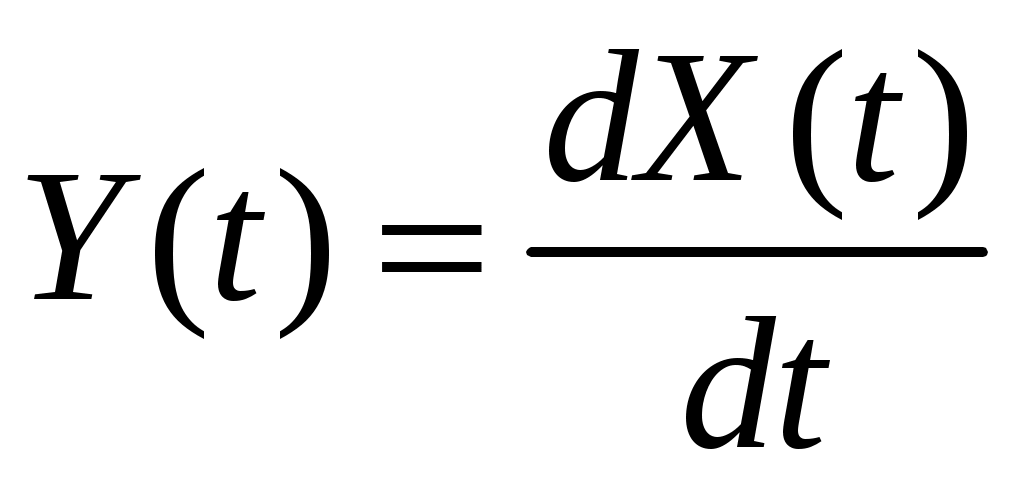 . .
В ариант № 25 ариант № 25
Стационарный случайный процесс  имеет спектральную плотность имеет спектральную плотность  , , 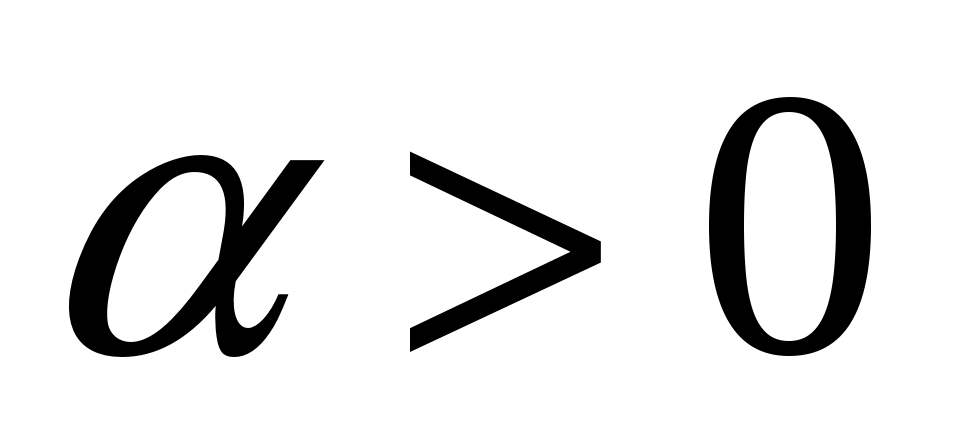 , ,  . Определить автоковариационную функцию и дисперсию случайного процесса . Определить автоковариационную функцию и дисперсию случайного процесса  . .
Вариант № 26
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию  , , 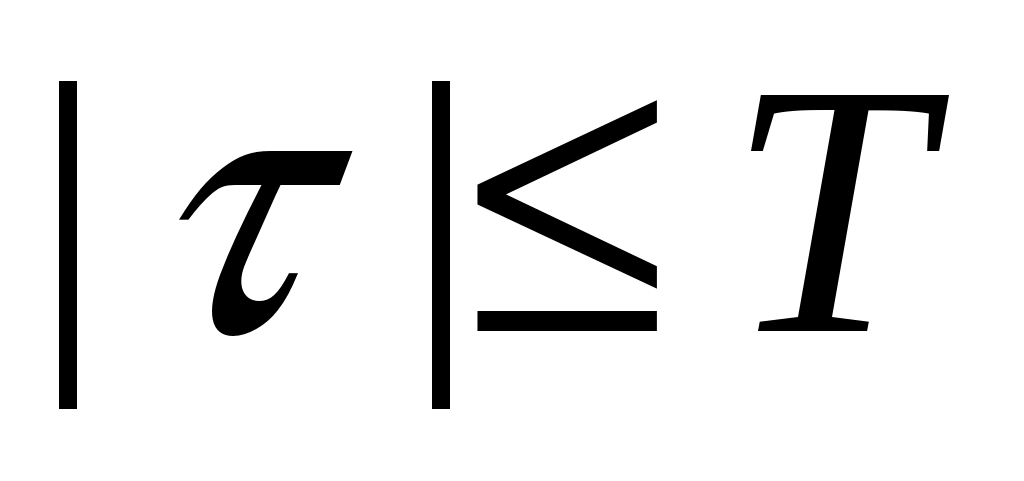 . Найти автоковариационную функцию случайного процесса . Найти автоковариационную функцию случайного процесса 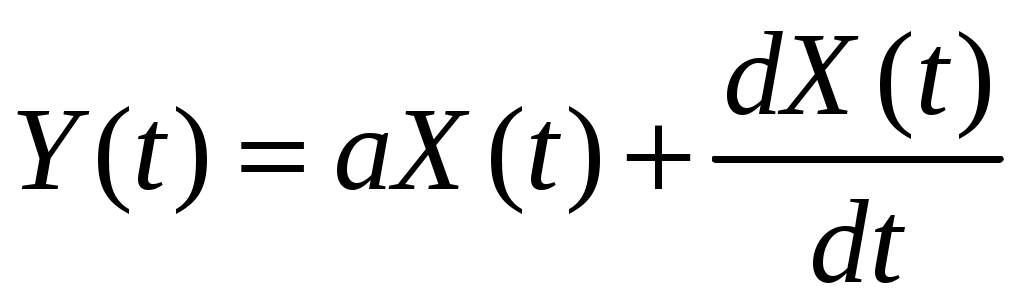 . .
Вариант № 27
Спектральная плотность 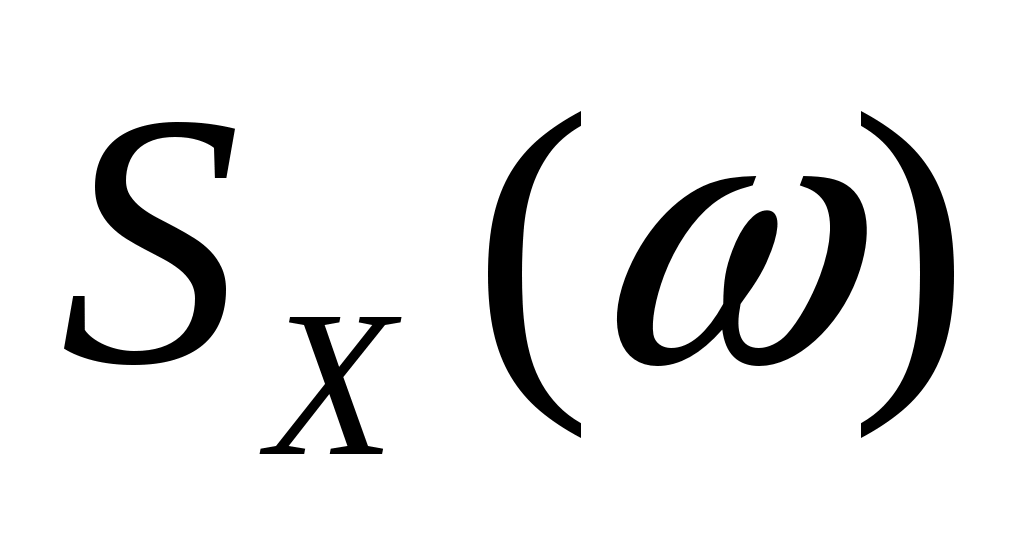 стационарного случайного процесса стационарного случайного процесса  имеет вид: имеет вид:  , , 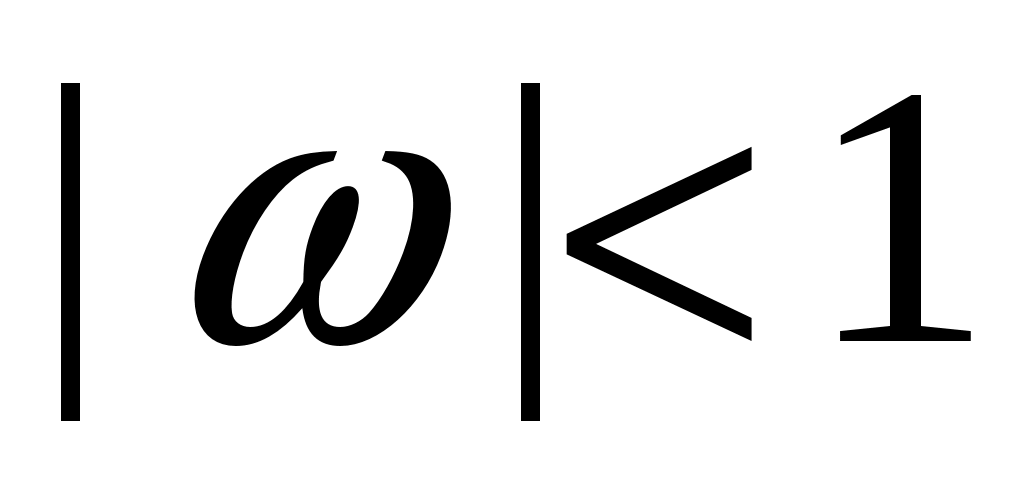 . Найти автоковариационную функцию, дисперсию и эффективную ширину спектра процесса . Найти автоковариационную функцию, дисперсию и эффективную ширину спектра процесса  . .
Вариант № 28
Найти спектральную плотность и эффективную ширину спектра стационарного случайного процесса  , если его автоковариационная функция имеет вид: , если его автоковариационная функция имеет вид: 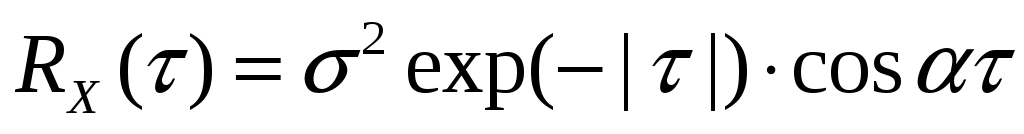 , , 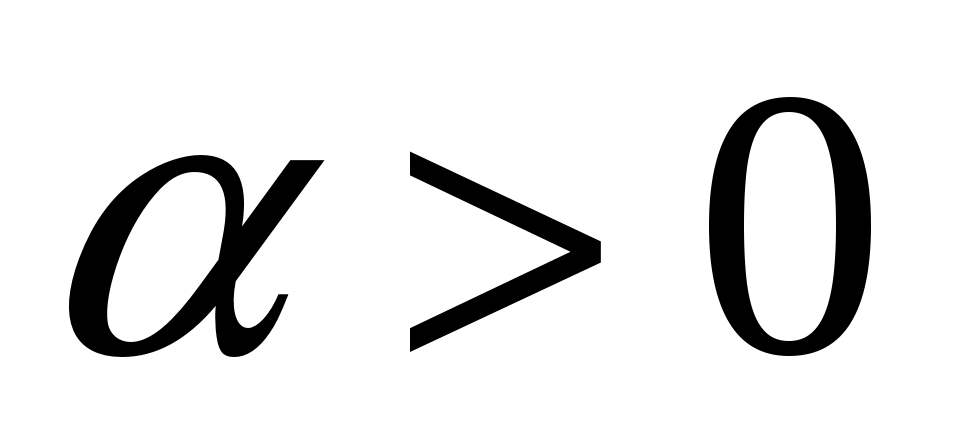 . .

Вариант № 29
Стационарный случайный процесс  имеет автоковариационную функцию имеет автоковариационную функцию 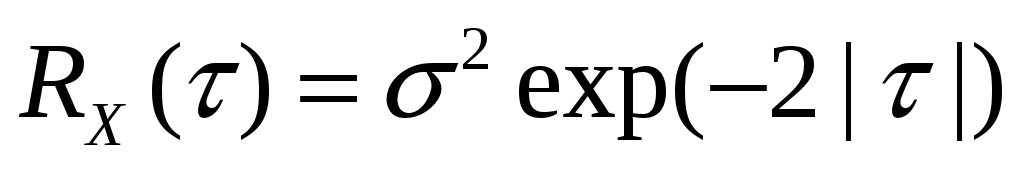 . Найти спектральную плотность . Найти спектральную плотность  случайного процесса случайного процесса 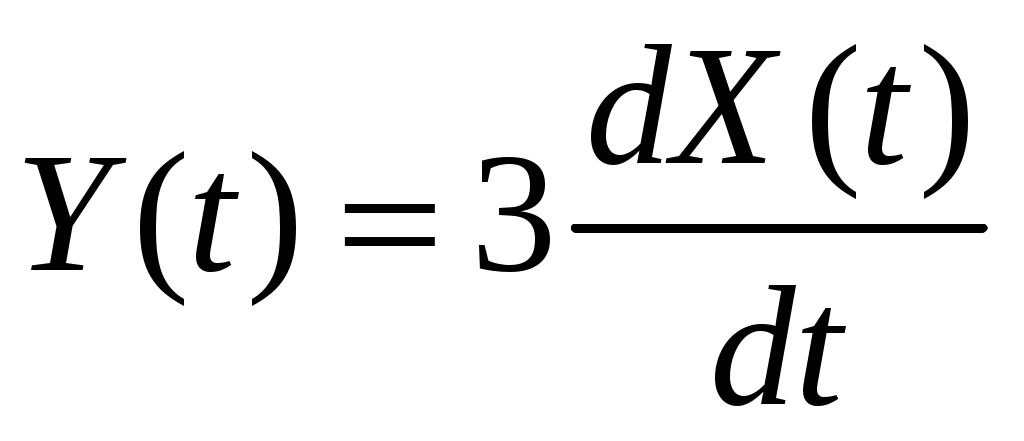 . .
Вариант № 30
Дана автоковариационная функция стационарного случайного процесса: 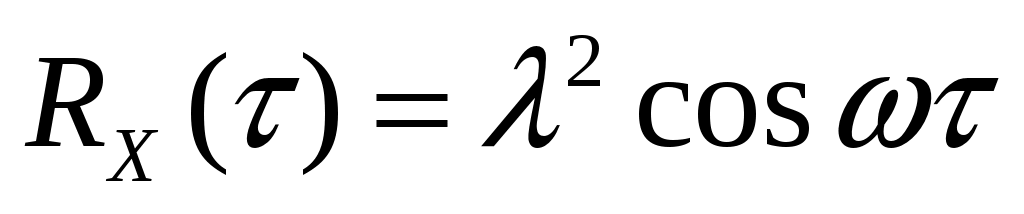 , , 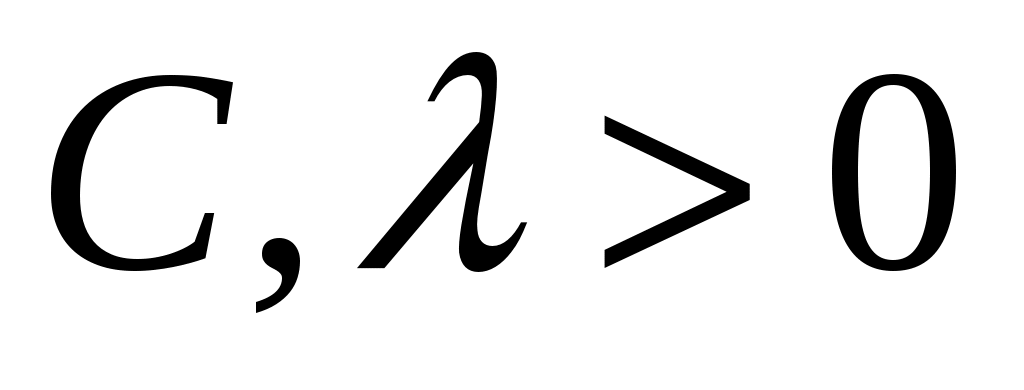 . Определить взаимную автоковариационную функцию случайных процессов . Определить взаимную автоковариационную функцию случайных процессов  и и 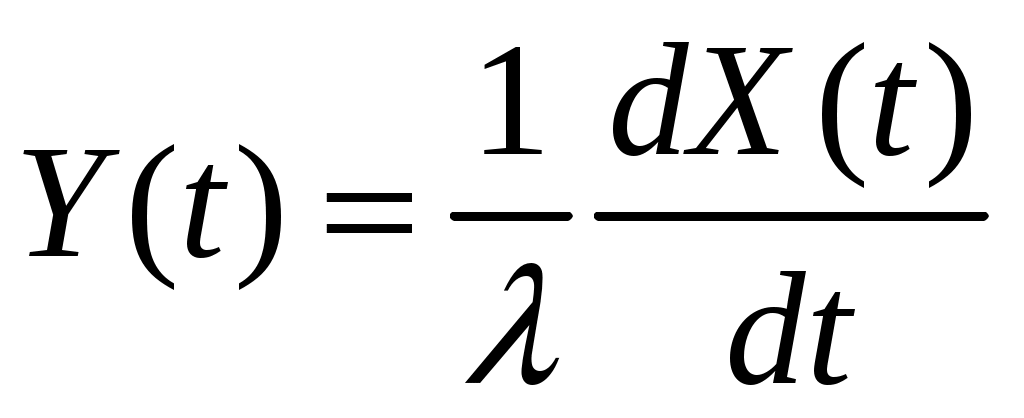 . . |
 Скачать 308.5 Kb.
Скачать 308.5 Kb.
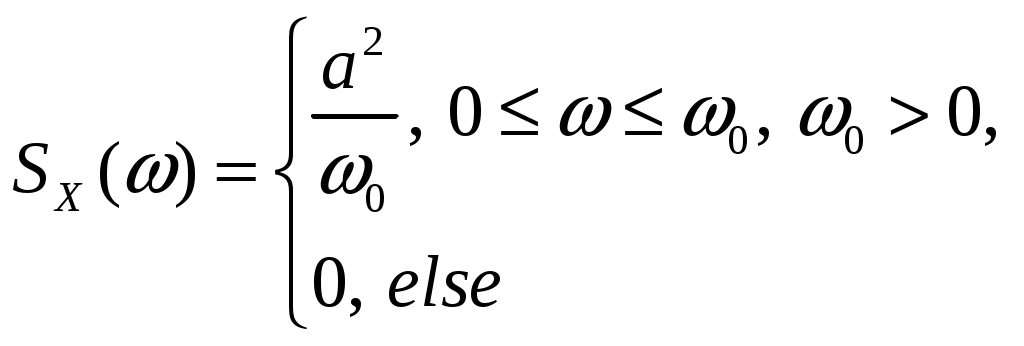 Определить автоковариационную функцию и дисперсию случайного процесса
Определить автоковариационную функцию и дисперсию случайного процесса 
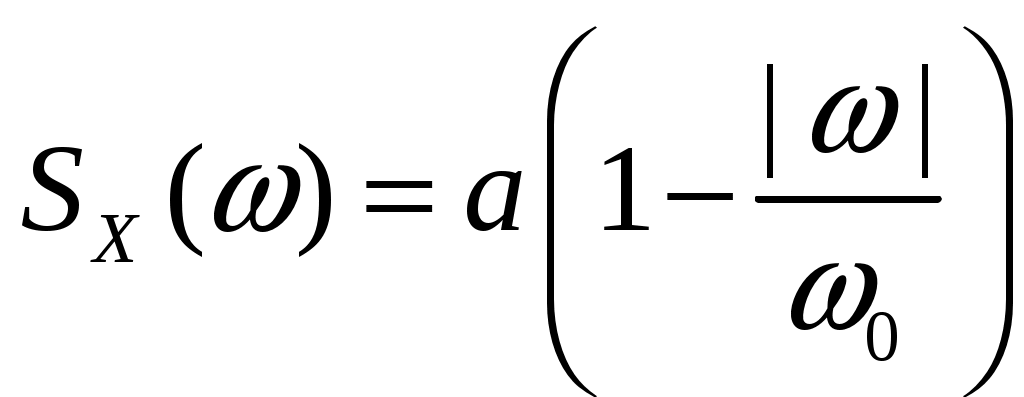 ,
,  ,
, 

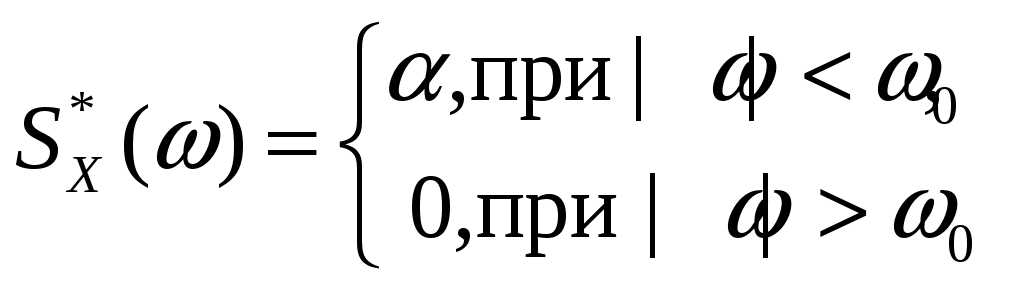 . Определить дисперсию
. Определить дисперсию  ариант № 25
ариант № 25
