Первообразная и неопределенный интеграл. Свойства неопределенног. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла
 Скачать 319.63 Kb.
|
|
Тема: Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Как найти функцию, производная которой известна? Возьмем для этого функцию  и выясним, для какой функции она производной, т.е. как найти функцию, прозводная которой была бы равна . Если искомую функцию условно обозначим через F(x), поставленный вопрос сводится к нахождению функции  , поскольку  .Определение:Функцию у= F (x) называют первообразной для функции у=f (x) на заданном промежутке Х, если для всех х ∈ Х выполняется равенство: F′(x) = f(x) В приведенном выше примере фунции является первообразной для функции на множестве (-∞;+∞), т.е. на всей числовой оси.  Рассмотрим f(x) = x2. Найдем производные следующих квадратичных функций: (х2)' = 2х, (х2 + 3)' = 2х, (х2 – 5)' = 2х – функции отличались между собой только постоянной, а производную имеют одну и ту же. Теорема. Если на каком-то промежутке функции F(x) и Ф(х) являются первообразными для одной и той же функции f(x), то на этом промежутке они отличаются друг от друга только на постоянное число. Ф(х)= F(x)+С Таким образом, если F′(x) = f (x)и С- любое постоянное число, тогда выражение F(x)+С также будет первообразным для функции f(x). Для нахождения первообразных используется следующая таблица. 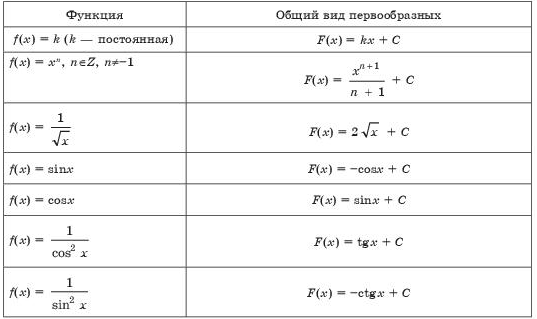 Операцию нахождения производной для заданной функции называют дифференцированием. Обратную операцию нахождения первообразной для данной функции называют интегрированием. Определение. Совокупность всех первообразных функции F(x)+С для данной функции f(x) называется неопределенным интегралом фунции f(x). Неопределенный интеграл обозначается:  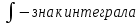 , f(x) — называют подынтегральной функцией; f(x)dx — называют подынтегральным выражением; x — называют переменной интегрирования;По опредению неопределенного интеграла получаем 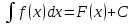 . Здесь вместо постоянной С можно взять любое число, т.е. ее значение точно не определено, поэтому интеграл и называется неопределеным интегралом.Операцию нахождения неопределенного интеграла называют интегрированием функции. Из определений первообразной и неопределенного интеграла следует, что 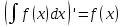 Из всего этого следует, то что нахождение производной и нахождение интеграла есть взаимообратные действия.  Свойства неопределённого интеграла Приведем примеры применения этих правил и свойств неопределенных интегралов.   Домашнее заадние: Перепишите необходимое и решите задачи. (Можете написать мне на ватсап в случае сложности) с помощью таблицы интегралов найдите неопределенный интеграл (таблицу интегралов можете посмотреть также во вложении документов)  |